概述
logistic回归和softmax回归都是在采用逻辑回归的思想来解决分类问题。
逻辑回归是一种二分类模型,用于解决二分类问题。它通过将输入特征与权重相乘并加上偏置项,然后将结果通过一个sigmoid函数(也称为logistic函数)映射到0到1之间的概率值,用于预测样本属于某一类别的概率。
softmax函数是一种常用的多类别分类激活函数。它可以将一组实数转化为概率分布,使得每个类别的概率值都在0到1之间且总和为1。softmax函数的计算公式是对输入向量中的每个元素进行指数运算,然后将结果进行归一化。
logistic softmax是一种常用的分类模型,常用于多类别分类任务。它是基于logistic regression(逻辑回归)和softmax函数的组合。
logistic softmax模型将逻辑回归和softmax函数结合在一起,用于解决多类别分类问题。它通过将每个类别与一个权重向量相乘,并加上偏置项,然后将结果通过softmax函数进行归一化,得到每个类别的概率值。最终,模型会预测样本属于概率最高的类别。
logistic softmax模型可以通过梯度下降等优化算法进行训练,调整权重和偏置项,使得模型能够更好地拟合训练数据,并在测试数据上进行准确的多类别分类预测。
几率(odd)
假设一个时间发生的概率为p,则
o
d
d
=
p
1
−
p
odd=\frac{p}{1-p}
odd=1−pp
二分类问题:一个问题发生和不发生就是一个最简单的二分类问题
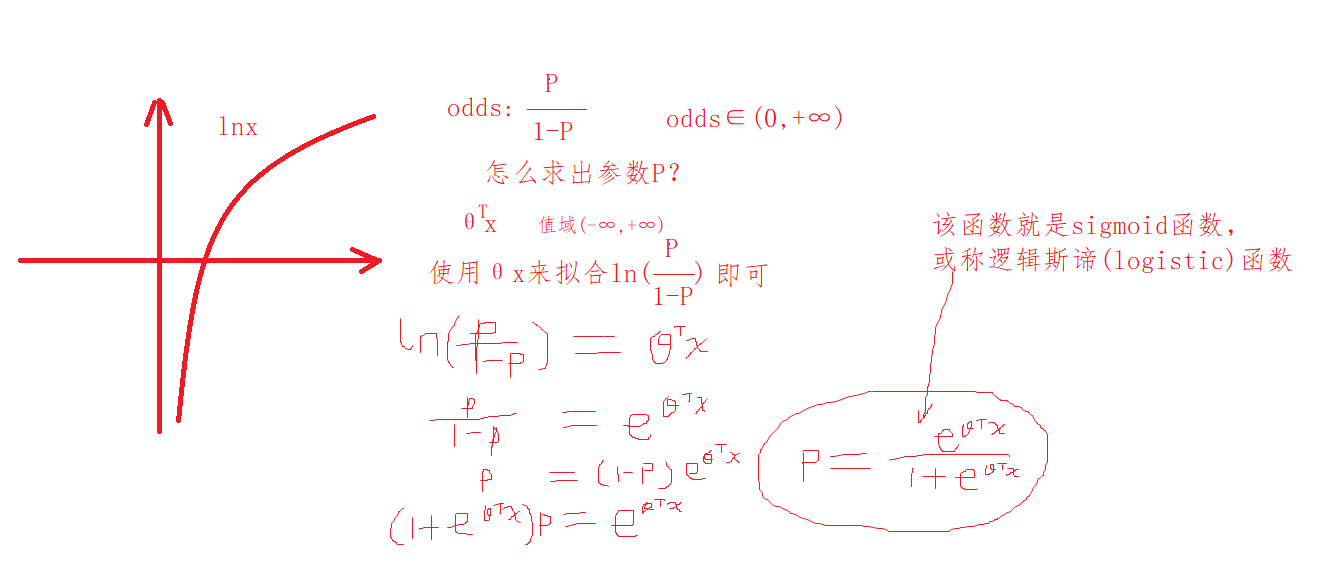
logistic回归
逻辑回归是一种二分类模型,用于解决二分类问题。它通过将输入特征与权重相乘并加上偏置项,然后将结果通过一个sigmoid函数(也称为logistic函数)映射到0到1之间的概率值,用于预测样本属于某一类别的概率。
逻辑回归也可以处理多分类问题,先采用ovr思想将多分类问题转为多个二分类问题,再采用逻辑回归思想进行处理。
logistic/sigmoid函数
- 目的是求解参数 θ
p
=
h
θ
(
x
)
=
g
(
θ
t
x
)
=
1
1
+
e
−
θ
t
x
y
=
{
1
0
y
^
=
{
1
,
p
>
t
h
r
e
s
h
o
l
d
0
,
p
≤
t
h
r
e
s
h
o
l
d
\begin{gathered} p=h_{θ}(x)=g(θ^tx)=\frac{1}{1+e^{-θ^tx}} \quad \\y=\left\{\begin{array}{l}1\\ 0\end{array} \,\quad\quad \hat{y}=\{\begin{array}{l}1,p>threshold\\ 0,p≤threshold\end{array} \right.\\ \end{gathered}
p=hθ(x)=g(θtx)=1+e−θtx1y={10y^={1,p>threshold0,p≤threshold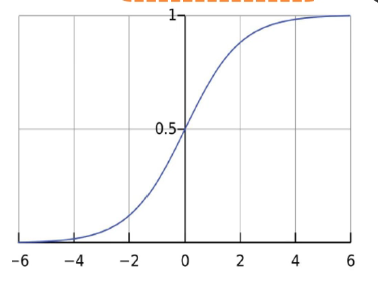
katex parse error: {align} can be used only in display mode.
重要:sigmoid函数的导数等于它本身乘以1减去它本身
g
′
(
z
)
=
g
(
z
)
(
1
−
g
(
z
)
)
g'(z)=g(z)(1-g(z))
g′(z)=g(z)(1−g(z))
logistic回归及似然函数


softmax回归
- softmax回归是logistic回归的一般化,适用于k分类的问题,针对每个类别都有一个参数向量θ,第k类类的参数为向量 θ k θ_{k} θk(特征),组成的二维矩阵为 θ k ∗ n θ_{k*n} θk∗n;
- softmax函数的本质就是将一个k维的任意实数向量压缩(映射)成另一个k维的实数向量,其中向量中的每个元素取值都介于(0, 1)之间。
- softmax回归概率函数为:
p ( y = k ∣ x ; θ ) = e θ k t x ∑ l = 1 k e l t x , k = 1 , 2 , . . . , k p(y=k|x;θ)=\frac{e^{θ_{k}^tx}}{\sum_{l=1}^{k}e_{l}^tx} ,\quad k=1,2,...,k p(y=k∣x;θ)=∑l=1keltxeθktx,k=1,2,...,k
softmax算法原理
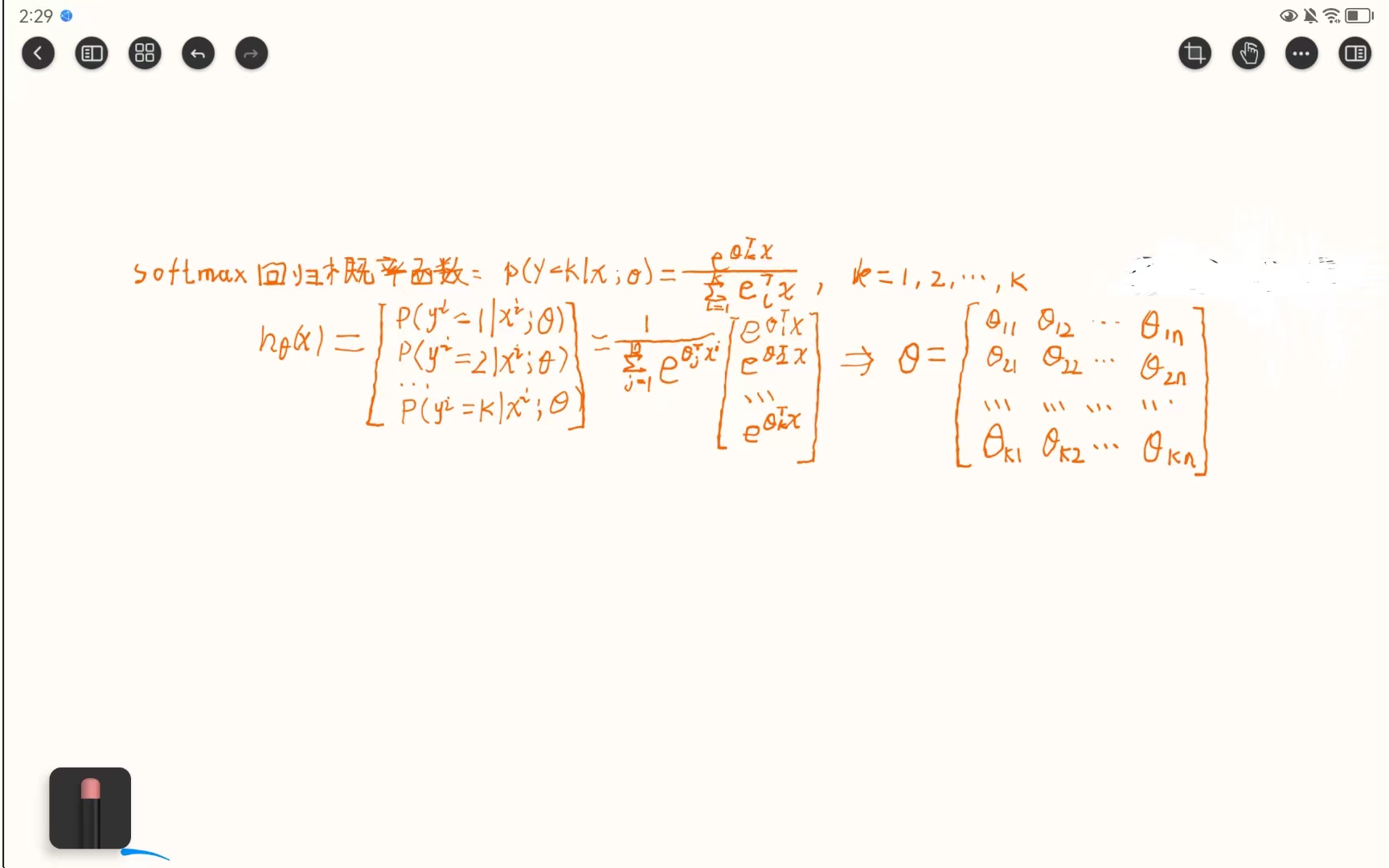
softmax算法损失函数

ovo和ovr思想
ovo和ovr是两种不同的思想或理论。当面对多类别分类问题时,ovo和ovr思想提供了两种不同的方法来解决这个问题。
先验概率和后验概率
先验概率(prior probability)是指在考虑任何新证据之前,根据以往的经验或已有的知识,对一个事件或假设的概率进行估计。
后验概率(posterior probability)是指在考虑了新的证据或信息之后,根据贝叶斯定理重新计算得到的概率。
先验概率和后验概率是贝叶斯统计推断的基础。贝叶斯定理通过先验概率和条件概率来计算后验概率,从而更新对事件或假设的概率估计。




发表评论