2024年机器学习 -- 初识决策树，web开发教程_机器学习

ajax

1)ajax请求的原理/ 手写一个ajax请求？
2)readystate？
3)ajax异步与同步的区别？
4)ajax传递中文用什么方法？

前12.png

1. 什么是特征选择

2. 熵

3. 条件熵

4. 信息增益

5. id3算法

6. 信息增益比

四、决策树生成

1. id3算法

五、决策树的剪枝（decision tree pruning）

1. 理想的决策树

2. 决策树面临的问题

3. 解决方法：剪枝

4. 判断剪枝的好坏

5. 决策树剪枝算法

6. cart算法

总结

一、概述

====

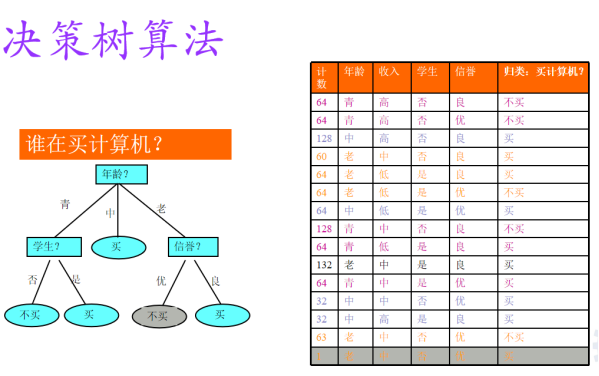
决策树是一种典型的分类方法

首先对数据进行处理，利用归纳算法生成可读的规则和决策树，然后使用决策对新数据进行分析。

本质上决策树是通过一系列规则对数据进行分类的过程。

1. 分类问题的步骤

（1）模型构建（归纳）通过对训练集合的归纳，建立分类模型。

（2）预测应用（推论）建立的分类模型，对测试集合进行测试。

2. 决策树的优点

（1）推理过程容易理解，决策推理过程可以表示成if then形式；

（2）推理过程完全依赖于属性变量的取值特点；

（3）可自动忽略目标变量没有贡献的属性变量，也为判断属性变量的重要性，减少变量的数目提供参考。

3. 决策树解决问题的一般方法

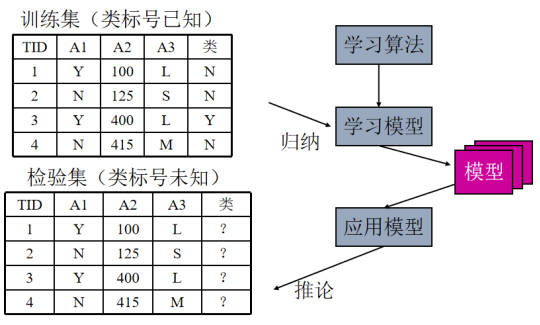
4. 决策树的3个步骤

如何确定每个分支节点，即选择特征
如何建立决策树，即决策树的生成
如何避免过拟合，即决策树的剪枝

5. 决策树的特点

叶子节点是结论
树的路径唯一确定了一个样例的判断过程
非叶子节点是特征

二、决策树建模与学习

==========

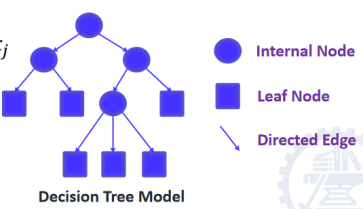
1. 什么是决策树

分类决策树选择器是树形结构，用于对样例分类，决策树的基本组成部分：决策结点（内部节点）、分支和叶子。

结点 – 内部节点：特征和属性

– 叶子节点：分类

有向边 – 特征的不同取值

决策树中最上面的结点称为根结点。是整个决策树的开始。

每个分支是一个新的决策结点，或者是树的叶子。

每个决策结点代表一个问题或者决策.通常对应待分类对象的属性。

每个叶结点代表一种可能的分类结果

在沿着决策树从上到下的遍历过程中，在每个结点都有一个测试。对每个结点上问题的不同测试输出导致不同的分枝，最后会达到一个叶子结点。这一过程就是利用决策树进行分类的过程，利用若干个变量来判断属性的类别。

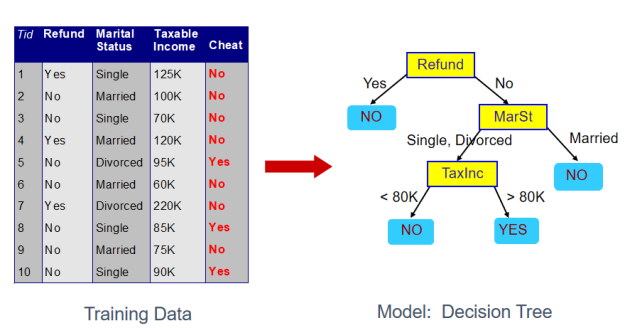
2. 决策树与if-then规则

从根节点开始对实例的每个特征进行测试，根据结果将其分支，递归的测试分配，直到叶子节点，从而构造了决策树。

决策树分类器的实质就是一系列的if-then规则

路径 — 规则

内部节点 — 判定规则

叶子节点 — 决策结论

****（1）性质：****互斥且完备（即：每个实例都是有且仅有一条路径或规则覆盖。）

（2）特点：

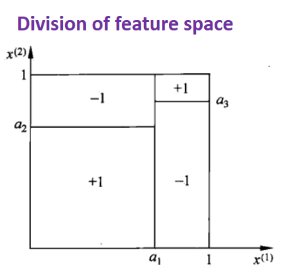
特征空间被划分为不相交的单元或区域。

条件概率分布: 在每个单元中定义的一个类的概率分布。

每个叶节点的条件概率都趋向于具有较高概率的一类。

当决策树进行分类时，该节点的实例被强制归入具有高条件概率的类别。

（3）例子：

（每个矩形是一个单元，假设只有正类和负类，判断条件概率大的就属于该类）

3. 如何学习一个决策树

对于数据集有n个特征，yi对应每个样例的类标签，n为容量

学习目标：构造一个决策树模型，通过训练实例对样本进行正确的分类

实质：从训练数据中归纳出一系列的if-then规则

目的: 构建与训练数据不一致程度较低、泛化能力较好的决策树。对未知数据有较好的预测，且训练精确度好

损失函数: (通常)正则化极大似然函数，使损失函数最小。

从所有候选中选择最优决策树是n-p难问题。在现实中，决策树学习通常采用一种启发式方法，即局部优化。

方法: 选取当前条件下的最优特征作为划分规则，即局部最优特征。主要有自顶向下，贪婪的搜索方法

算法步骤：

（1）建立根节点（选择最佳特征）

（2）对于每个分支确定下一个特征，从而对节点进行划分

（3）确立下一个特征，递归的方法构造决策树

决策树学习算法包括:

（1）特征选择

（2）决策树生成

（3）决策树修剪(避免过拟合)

决策树: 一个条件概率分布。不同的决策树对应不同复杂度的概率模型。

决策树生成: 模型的局部选择(考虑局部优化)

决策树剪枝: 模型的全局选择(考虑全局优化)

三、特征选择

======

1. 什么是特征选择

特征选择: 选择能够对训练数据进行分类的特征。决定使用哪个特征来划分特征空间。如果一个特征分类的结果与随机分类的结果相似，那么这个特征就不能进行分类。

我们如何选择最好的特性? 特征选择准则：信息增益

哪一个特征最好? 它会生成最小损失的树；启发式:选择产生“最纯粹”节点的特性

策略: 选择能够获得最大信息增益的特性

2. 熵

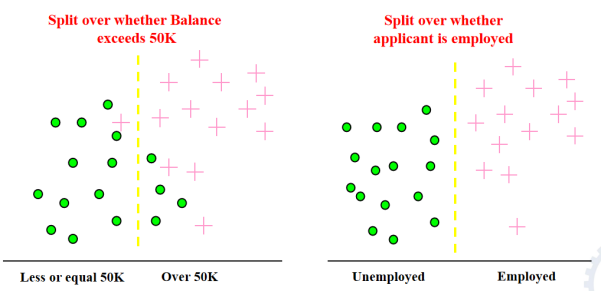
引入‘熵’的概念，看下图哪一个信息量更大？

左边图信息量更大，因为它有混合的，不确定性更改可以帮助我们更好的分类

熵越大，不确定性越大。

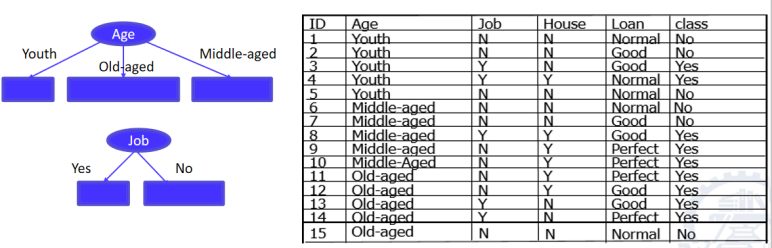
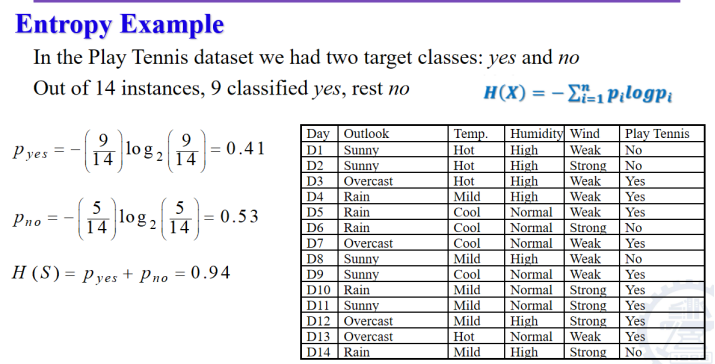
例子：在数据集中，我们有四个特性和两个目标类。在15个实例中，9个分类为是，其余为否有一些方法可以选择特性。如:

熵：用于测量随机变量的不确定性。熵越大，不确定性越大。

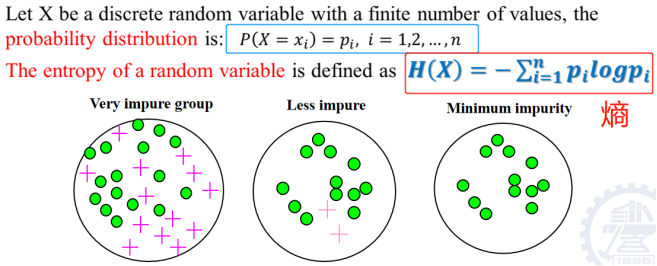
当只有两个特征，变化为二项分布

3. 条件熵

如果是多个特征 --> 引入条件熵类似于联合概率密度，又叫经验熵或经验条件熵。

4. 信息增益

有了熵和经验熵 --> 信息增益

表示：以某特征划分数据集前后的熵的差值

在训练集d上特征a的信息增益g(d,a)表示为d的熵h(d)和条件熵h(d|a)的差值。

因此，特征选择的方法就是要使用信息增益的ig3算法，选择最小信息增益的特征。

5. id3算法

使用ig来确定节点特征。

定义变量：

d: 训练数据 |d|：样例的总个数

k: 总共的类别，ck分别表示每个类，|ck|表示每个类对应的个数

假设特征a有n个值，则将d划分为{d1，d2，… dn}子集，每个子集中有不同类dik

算法表示：

输入：训练集d和特征a

输出：在训练集d上，特征a的信息增益g(d, a)

计算训练集d的熵h(d)
计算特征a的条件熵 h(d,a)
计算信息增益g(d, a) = h(d) - h(d,a)

例题：

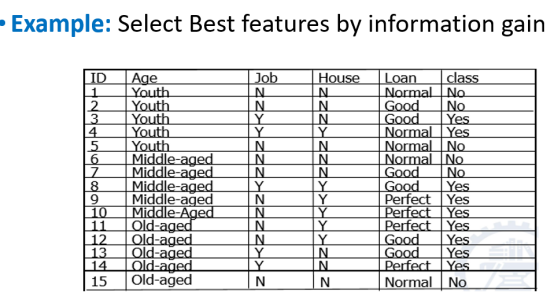
6. 信息增益比

由于信息增益偏向于特征取值多的特征，具有倾向性，因此为了对其修正提出了：信息增益比。

总结： ig（信息增益）id3算法

igr（信息增益比）c4.5算法

css

1，盒模型
2，如何实现一个最大的正方形
3，一行水平居中，多行居左
4，水平垂直居中
5，两栏布局，左边固定，右边自适应，左右不重叠
6，如何实现左右等高布局
7，画三角形
8，link @import导入css
9，bfc理解

js

1，判断 js 类型的方式
2，es5 和 es6 分别几种方式声明变量
3，闭包的概念？优缺点？
4，浅拷贝和深拷贝
5，数组去重的方法
6，dom 事件有哪些阶段？谈谈对事件代理的理解
7，js 执行机制、事件循环
8，介绍下 promise.all
9，async 和 await,
10，es6 的 class 和构造函数的区别
11，transform、translate、transition 分别是什么属性？css 中常用的实现动画方式,
12，介绍一下raf(requestanimationframe)
13，javascript 的垃圾回收机制讲一下,
14，对前端性能优化有什么了解？一般都通过那几个方面去优化的？