第6课:逻辑回归lr与广义线性模型glm开发实践
背景知识-lr/glm应用场景及原理
逻辑回归(lr)
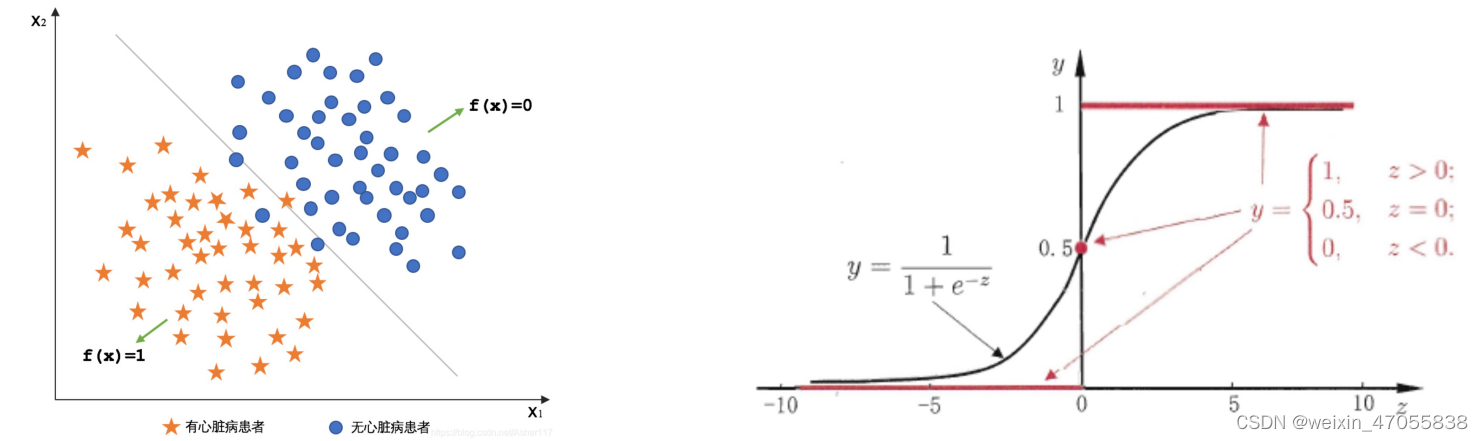
二分类问题:逻辑回归
- 数据进行二元分类:例如对病人的数据进行疾病诊断。
- 预测某件事情发生的概率:例如预测一个网站的用户变成付费用户的概率。
广义线性模型(glm)
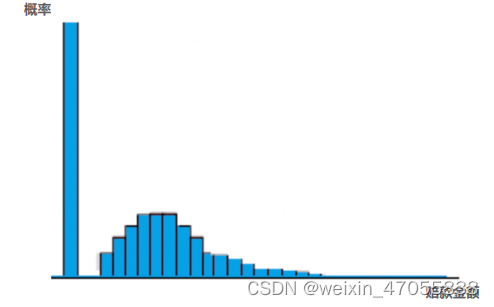
举例: 风险保费预测,根据要提供的保障责任,计算预期总索赔额
-
直接对纯保费建模
- tweedie 分布(1,2)
-
也可以通过两步建模间接近似:纯保费 = 索赔次数 * 平均索赔金额
- 索赔次数:泊松分布、负二项分布
- 平均索赔金额:伽马分布、逆高斯分布
回顾一下线性回归:它是glm的一个基本形式,其假设响应变量 y 的真实值由两部分组成
y a c t u a l = β 0 + x 1 β 1 + x 2 β 3 + . . . + x p β p + ϵ y_{actual} = \beta_0+x_1\beta_1+x_2\beta_3+...+x_p\beta_p+\epsilon yactual=β0+x1β1+x2β3+...+xpβp+ϵ
系统组件( system component ):线性预测器 η = x t β \eta = x^t\beta η=xtβ
误差组件( error component ):白噪声 ϵ ∼ n ( 0 , 1 ) \epsilon \sim n(0, 1) ϵ∼n(0,1) (高斯随机变量)
线性回归:响应变量 y的条件分布为高斯分布
y
∼
n
(
x
t
,
1
)
y\sim n(x^t, 1)
y∼n(xt,1)
而对于glm,
glm允许误差项的概率分布扩展为指数分布族: 伯努利分布 (逻辑回归),泊松分布,gamma分布,复合泊松gamma 分布,tweedie分布等
glm 有三个组件
- 系统组件 η = x t β \eta = x^t\beta η=xtβ, 与lm 中一致
- 随机组件:是一个指数族分布作为响应变量y的概率分布 p ( y ; θ ) p(y;\theta) p(y;θ)
- 连接函数:使得 η = g ( μ ) \eta=g(\mu) η=g(μ), 描述系统组件和随机组件之间的关系
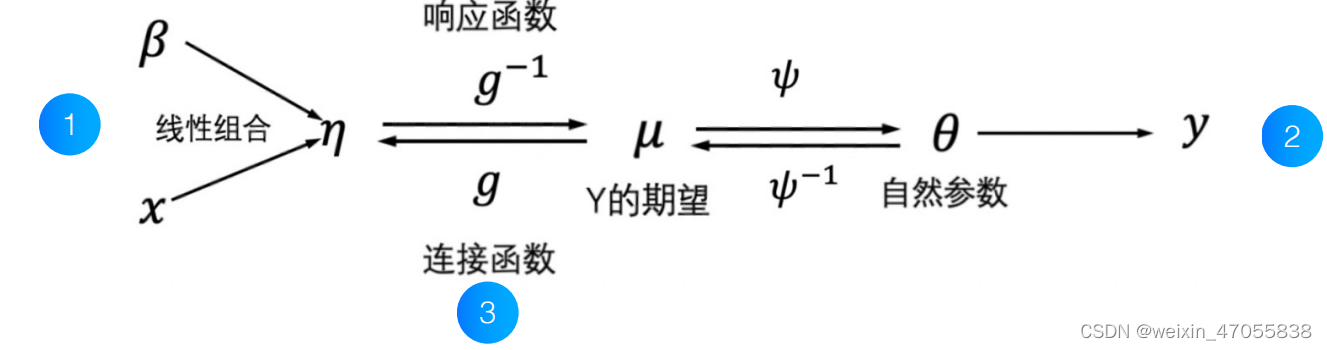
连接函数的种类大致有一下三种
| 名称 | 连接函数 | 激活函数(反连接函数) | μ 的空间 \mu 的空间 μ的空间 |
|---|---|---|---|
| identity | η = μ \eta=\mu η=μ | μ = η \mu=\eta μ=η | μ ∈ r \mu \in r μ∈r |
| logit | η = ln { μ 1 − μ } \eta=\ln \{\frac{\mu}{1-\mu}\} η=ln{1−μμ} | μ = e η 1 + e η \mu=\frac{e^\eta}{1+e^\eta} μ=1+eηeη | μ ∈ ( 0 , 1 ) \mu \in (0, 1) μ∈(0,1) |
| log | η = ln ( μ ) \eta=\ln(\mu) η=ln(μ) | μ = e η \mu=e^\eta μ=eη | μ > 0 \mu>0 μ>0 |
隐语模型-密态sslr/ssglm
优化器
一阶优化器
二阶优化器
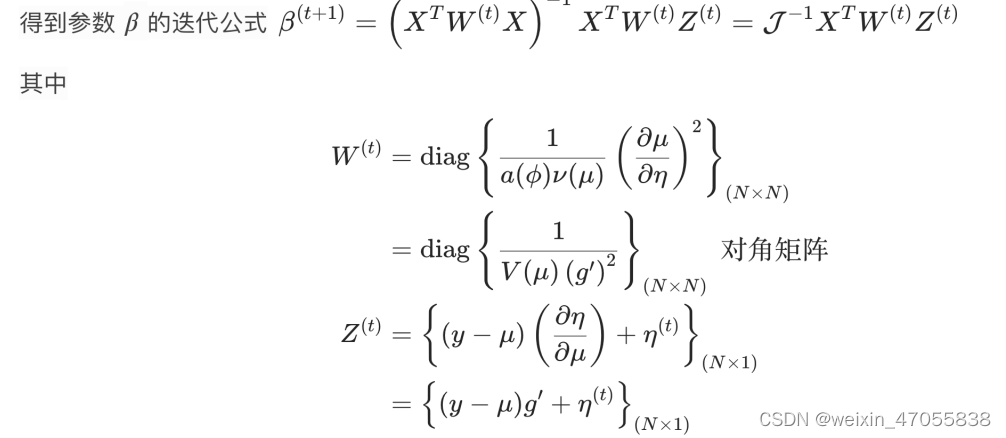
二阶优化器的优点: 初始化准确 收敛速度快
缺点: 计算/通信复杂度高
可以结合着用,二阶优化器 + 一阶优化器
secret sharing
加法实现
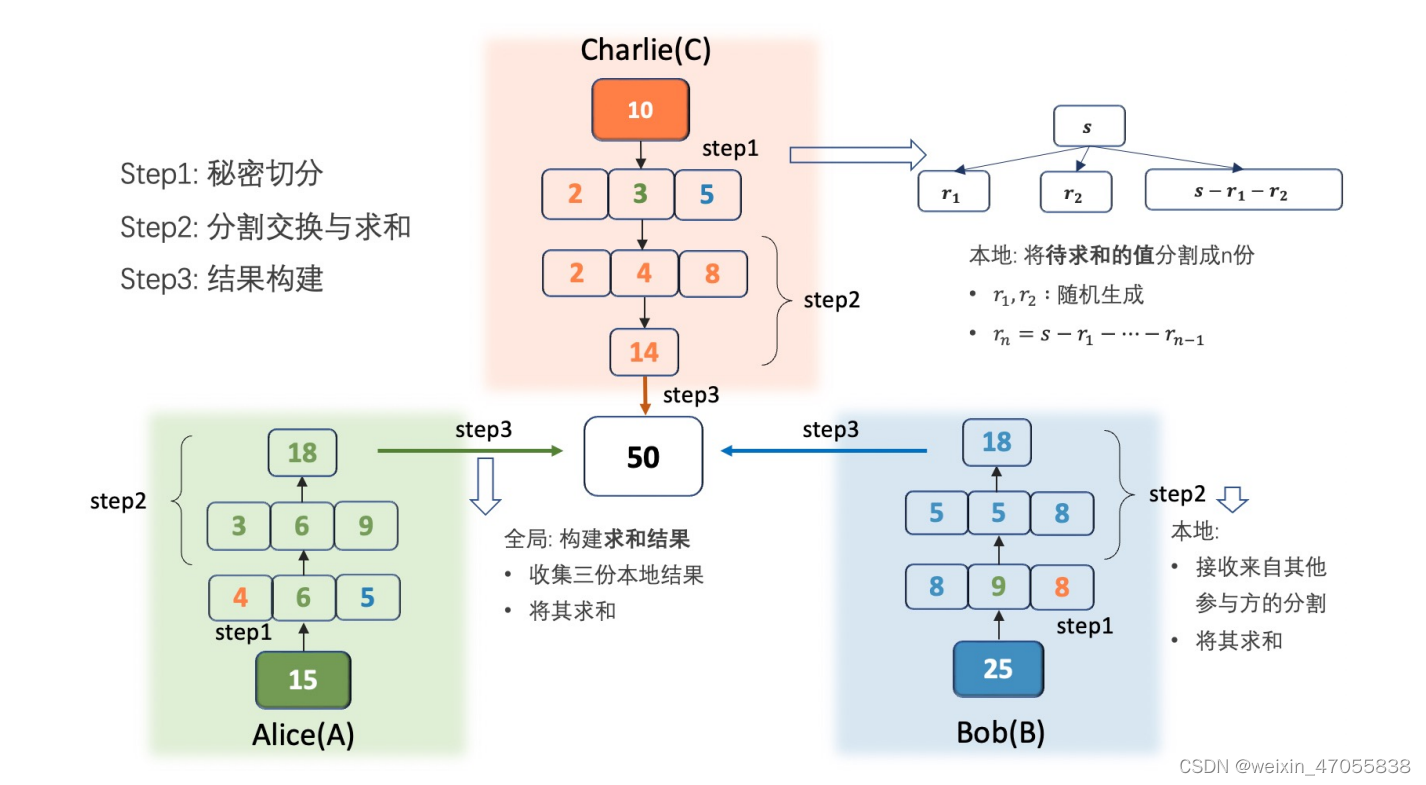
乘法实现
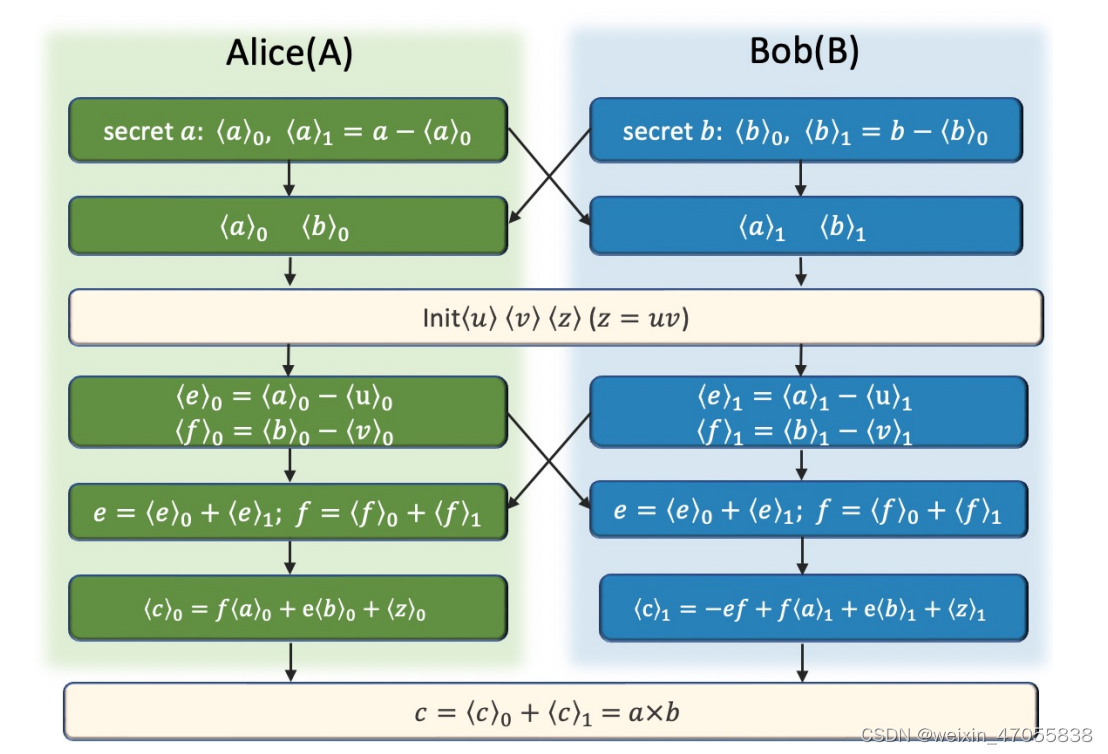
应用实现-从理论到隐语应用
sslgm 参数解析
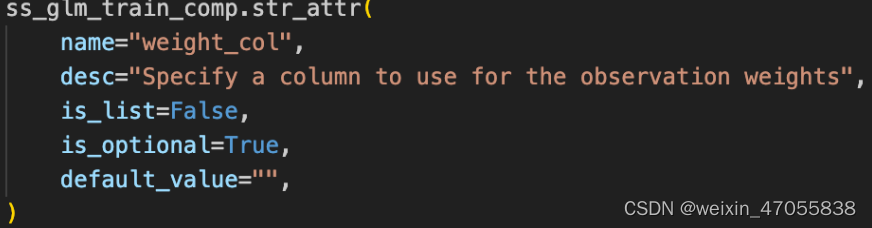
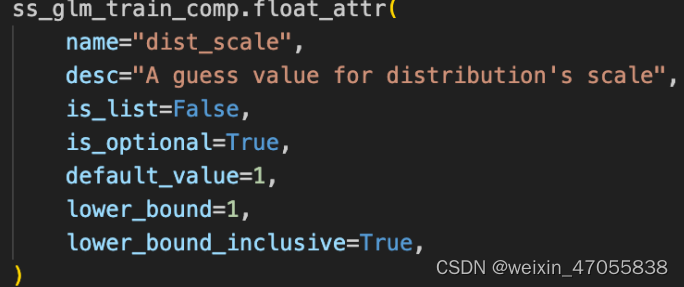
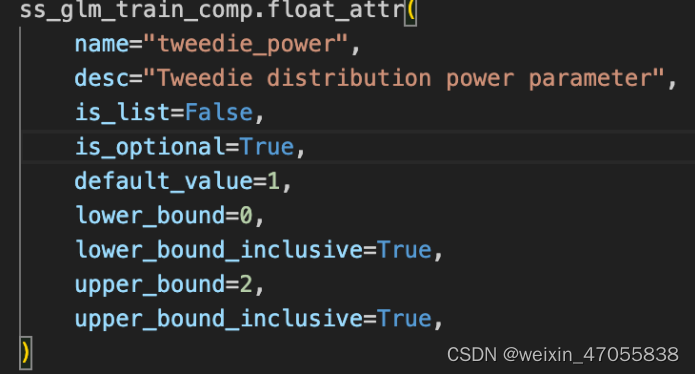
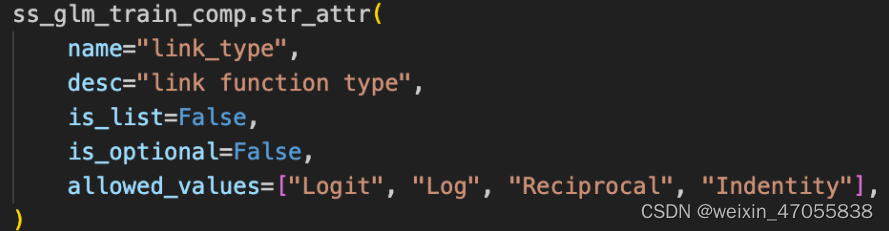
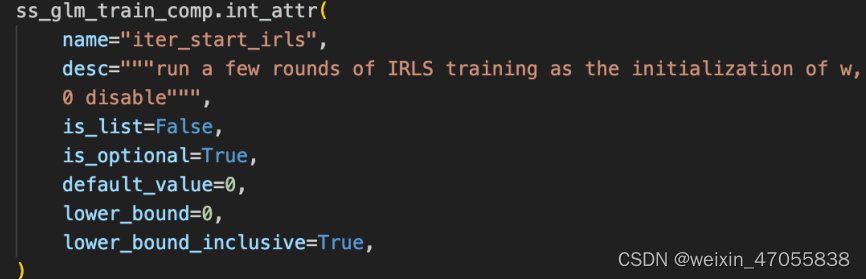
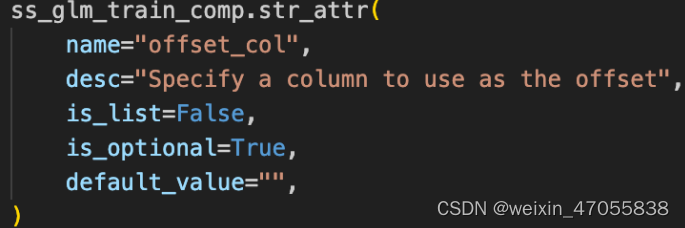

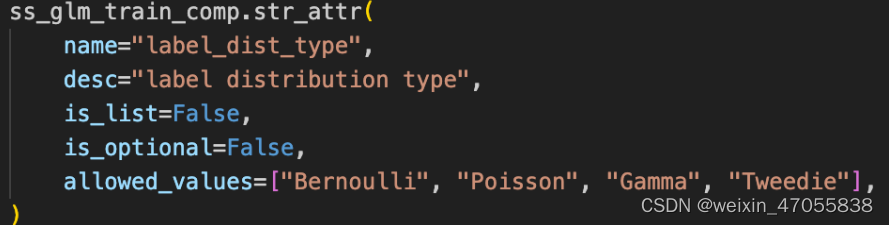
ss-lr / ssglm 在隐语实现有什么独特优势?
- 可证安全
- 不依赖可信第三方
- 支持多种模型(伯努利分布(逻辑回归),泊松分布,gamma分布,tweedie分布)
- 计算高效




发表评论