我要评论目录
一. 逻辑回归（logistic regression）
逻辑回归是一个非常经典的解决分类问题的机器学习方法，该算法的主要思想是将输入变量的线性组合映射到0到1之间的概率，用于预测二元输出变量。
二. 逻辑回归模型的算法原理
1. 处理数据
假设我们有一个二分类问题，需要预测一个样本属于两个类别中的哪一个。
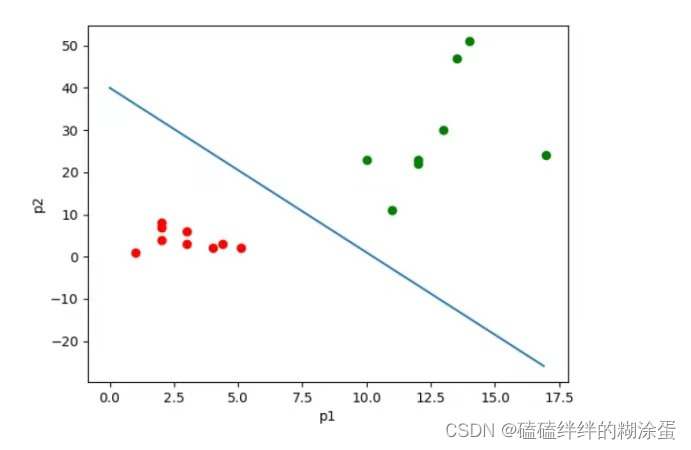
2. 引入sigmoid函数
1）公式：
2）sigmoid图像：
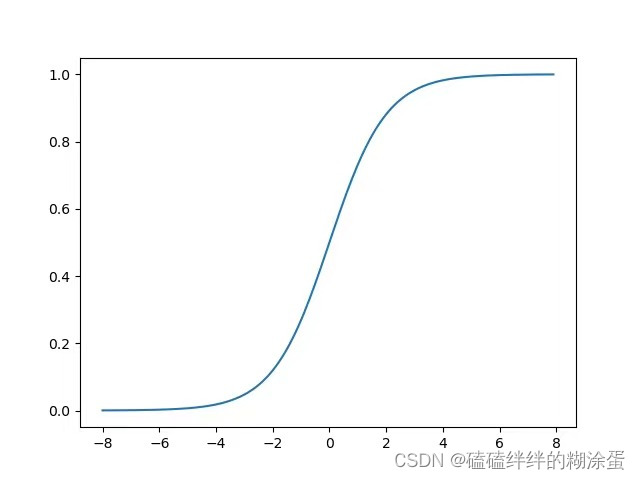
注：将线性回归的结果映射到[0,1]区间上，实质上就是完成了二分类任务。
3. 引入梯度下降法
梯度下降法通过反复迭代来最小化损失函数，直至找到最优解，起到了优化模型参数、寻找最优解、调节学习率和处理大规模数据的作用。是逻辑回归模型中常用的优化算法之一，能够有效地提升模型的性能。
其中，损失函数公式为：，
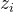是第i个样本的线性组合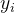，是对应的类别标签（0或1）。
三. 逻辑回归与线性回归的相同点和不同点
1）相同点：
逻辑回归与线性回归都是一种广义线性模型（generalized linear model）。
2）不同点：
1）逻辑回归假设因变量 y 服从伯努利分布，而线性回归假设因变量 y 服从高斯分布。
2）逻辑回归用于分类问题，线性回归用于拟合回归问题。
注：逻辑回归算法去除sigmoid映射函数就是一个线性回归。也就是说，逻辑回归以线性回归为理论支持，并通过sigmoid函数引入了非线性因素，可以轻松处理0/1分类问题。
四. 算法实现
1. 导入包
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
2. 定义随机数种子
# 设置随机种子
seed_value = 2023
np.random.seed(seed_value)
3. 定义逻辑回归模型
3.1 初始化模型
# 初始化参数
self.weights = np.random.randn(x.shape[1])
self.bias = 0
3.2 正向传播
# 计算sigmoid函数的预测值, y_hat = sigmoid(w * x + b)
y_hat = sigmoid(np.dot(x, self.weights) + self.bias)
3.3 损失函数
# 计算损失函数
loss = (-1 / len(x)) * np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat))
3.4 反向传播
# 计算梯度
dw = (1 / len(x)) * np.dot(x.t, (y_hat - y))
db = (1 / len(x)) * np.sum(y_hat - y)
# 更新参数
self.weights -= self.learning_rate * dw
self.bias -= self.learning_rate * db
3.5 模型预测
# 预测
def predict(self, x):
y_hat = sigmoid(np.dot(x, self.weights) + self.bias)
y_hat[y_hat >= 0.5] = 1
y_hat[y_hat < 0.5] = 0
return y_hat
3.6 模型精度
# 精度
def score(self, y_pred, y):
accuracy = (y_pred == y).sum() / len(y)
return accuracy
3.7 用鸢尾花数据集来预测模型
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# 设置随机种子
seed_value = 2023
np.random.seed(seed_value)
# sigmoid激活函数
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 定义逻辑回归算法
class logisticregression:
def __init__(self, learning_rate=0.003, iterations=100):
self.learning_rate = learning_rate # 学习率
self.iterations = iterations # 迭代次数
def fit(self, x, y):
# 初始化参数
self.weights = np.random.randn(x.shape[1])
self.bias = 0
# 梯度下降
for i in range(self.iterations):
# 计算sigmoid函数的预测值, y_hat = w * x + b
y_hat = sigmoid(np.dot(x, self.weights) + self.bias)
# 计算损失函数
loss = (-1 / len(x)) * np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat))
# 计算梯度
dw = (1 / len(x)) * np.dot(x.t, (y_hat - y))
db = (1 / len(x)) * np.sum(y_hat - y)
# 更新参数
self.weights -= self.learning_rate * dw
self.bias -= self.learning_rate * db
# 打印损失函数值
if i % 10 == 0:
print(f"loss after iteration {i}: {loss}")
# 预测
def predict(self, x):
y_hat = sigmoid(np.dot(x, self.weights) + self.bias)
y_hat[y_hat >= 0.5] = 1
y_hat[y_hat < 0.5] = 0
return y_hat
# 精度
def score(self, y_pred, y):
accuracy = (y_pred == y).sum() / len(y)
return accuracy
# 导入数据
iris = load_iris()
x = iris.data[:, :2]
y = (iris.target != 0) * 1
# 划分训练集、测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.15, random_state=seed_value)
# 训练模型
model = logisticregression(learning_rate=0.03, iterations=1000)
model.fit(x_train, y_train)
# 结果
y_train_pred = model.predict(x_train)
y_test_pred = model.predict(x_test)
score_train = model.score(y_train_pred, y_train)
score_test = model.score(y_test_pred, y_test)
print('训练集accuracy: ', score_train)
print('测试集accuracy: ', score_test)
# 可视化决策边界
x1_min, x1_max = x[:, 0].min() - 0.5, x[:, 0].max() + 0.5
x2_min, x2_max = x[:, 1].min() - 0.5, x[:, 1].max() + 0.5
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max, 100), np.linspace(x2_min, x2_max, 100))
z = model.predict(np.c_[xx1.ravel(), xx2.ravel()])
z = z.reshape(xx1.shape)
plt.contourf(xx1, xx2, z, cmap=plt.cm.spectral)
plt.scatter(x[:, 0], x[:, 1], c=y, cmap=plt.cm.spectral)
plt.xlabel("sepal length")
plt.ylabel("sepal width")
plt.show()
五. 逻辑回归的优缺点
1.优点
- 简单高效：逻辑回归模型相对简单，计算速度快，适用于处理大规模数据集。
- 可解释性强：逻辑回归可以提供概率预测结果，可以解释特征对预测结果的影响程度。
- 对稀疏数据友好：逻辑回归对于具有大量稀疏特征的数据集，表现较好。
- 适用性广泛：逻辑回归可以用于二分类问题，也可以通过扩展到多类别问题。
- 适用于线性可分问题：当样本数据近似线性可分时，逻辑回归模型能够取得较好的分类效果。
2. 缺点
- 假设线性关系：逻辑回归是一种线性模型，假设特征和目标之间存在线性关系。当数据具有复杂的非线性关系时，逻辑回归可能表现较差。
- 对异常值敏感：逻辑回归对异常值较为敏感，特别是在特征空间较小的情况下，异常值可能对模型的性能产生较大影响。
- 高度依赖特征选择：逻辑回归的性能和特征选择密切相关。选择不好的特征可能导致模型欠拟合或过拟合。
- 无法处理非线性关系：逻辑回归本身是一种线性分类器，对于非线性关系的数据，逻辑回归模型无法很好地拟合。
发表评论