目录
题目:p1149 [noip2008 提高组] 火柴棒等式 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
写在前面:
怎么样才能学好一个算法?
我个人认为,系统性的刷题尤为重要,
所以,为了学好深度优先搜索,为了用好暴搜应对蓝桥杯,
事不宜迟,我们即刻开始刷题!
题目:p1149 [noip2008 提高组] 火柴棒等式 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目描述:

输入格式:
一个整数 n ( 1 ≤ n ≤ 24 )。
输出格式:
一个整数,能拼成的不同等式的数目。
输入样例:
1.
142.
18输出样例:
1.
22.
9解题思路:
我们使用深度优先搜索的时候,
第一个要注意的点是搜索的顺序,
因为我们要保证,
我们写出的递归结构能够遍历所有情况,
在我们初学搜索的时候,我们一定要画一个递归搜索树观察,
递归非常抽象,画图能很好的帮助我们解题。(以上递归搜索的基本思路,多熟悉总是好的)
接下来是具体思路:
根据题意可知:

这样,我们可以把它想象成,
在abc这三个位置上填数字,
满足a+b=c以及a+b+c的火柴数等于n-4,
那我们根据这个思路来画递归搜索数:
根节点:
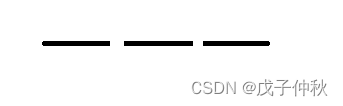
往第一个位置填数字:
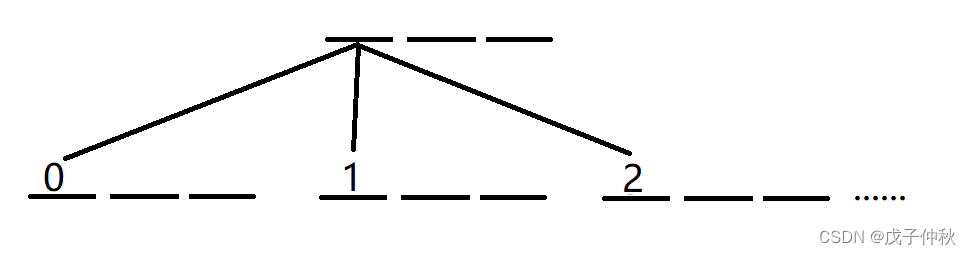 继续往下递归搜索,
继续往下递归搜索,
我们发现其实这是一个指数型的枚举:
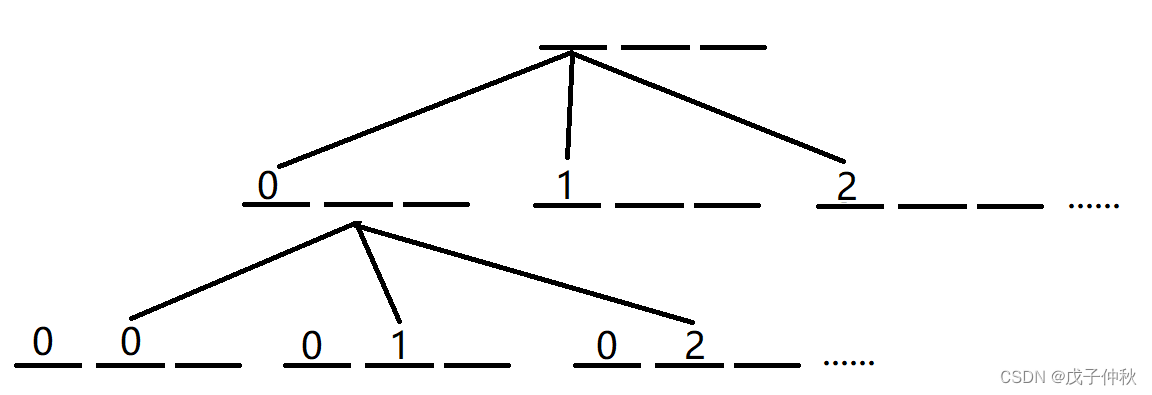 我们继续往下搜索:
我们继续往下搜索:
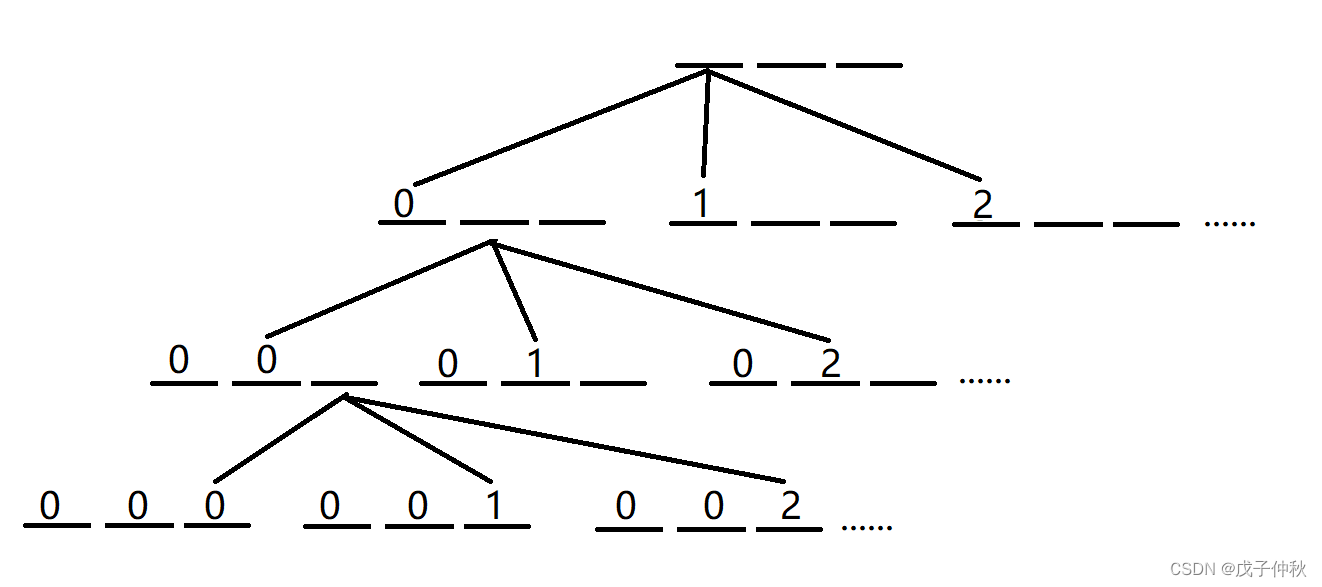
以此类推,我们能够搜索出所有的情况,
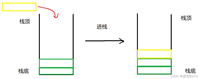
然后再根据题意进行判断和剪枝:
剪枝:
如果a或者a+b的火柴数已经大于题目要求的n,
就直接return,也就是剪枝。
接下来看代码:
代码:
//包常用头文件
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
//题目n最大是24,如果不确定该开多大,那就开大点
const int n = 10010;
int n;
//计数最后输出
int res = 0;
int st[n];
//各个数字的火柴数
int match[10010] = { 6, 2, 5, 5, 4, 5, 6, 3, 7, 6 };
void dfs(int u, int sum)
{
//如果a或者a+b的火柴数已经大于题目要求的n,剪枝
if(sum > n)
return;
if (u > 3)
{
//满足a+b=c以及a+b+c的火柴数等于n-4
if (st[1] + st[2] == st[3] && sum == n - 4)
{
res++;
}
return;
}
//搜索
for (int i = 0; i < 1000; i++)
{
st[u] = i;
dfs(u + 1, sum + match[i]);
st[u] = 0;
}
}
int main()
{
scanf("%d", &n);
//递推取得每个数字的火柴数
for(int i = 10; i < 1000; i++)
{
match[i] = match[i / 10] + match[i % 10];
}
dfs(1, 0);
printf("%d", res);
return 0;
}
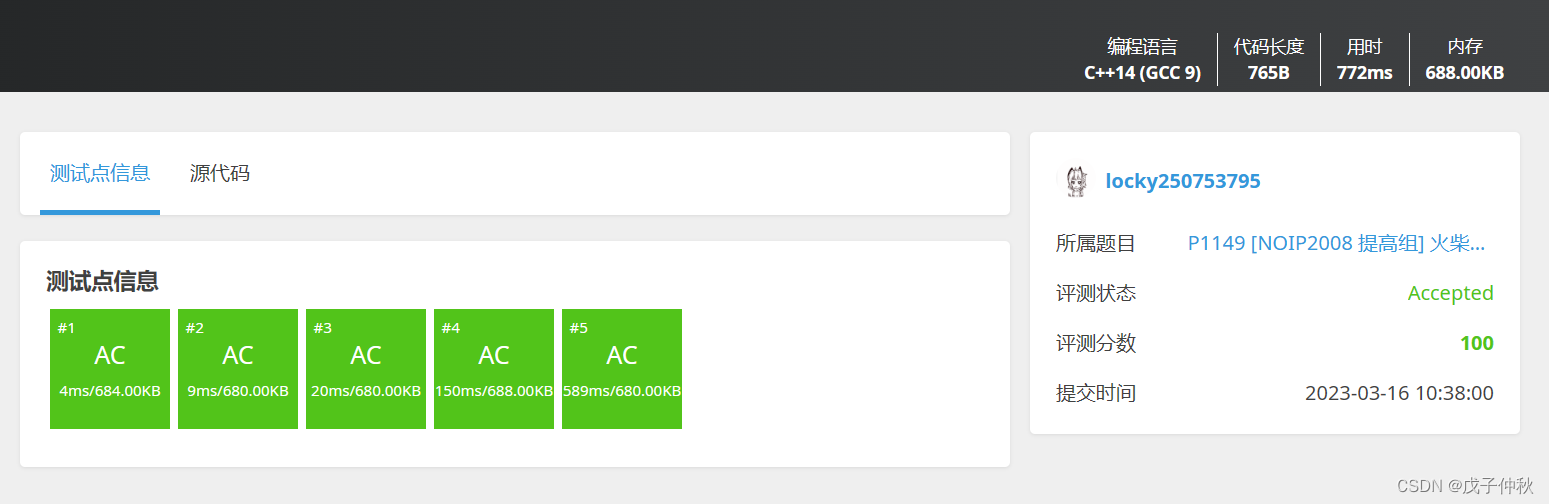
ac !!!!!!!!!!
写在最后:
以上就是本篇文章的内容了,感谢你的阅读。
如果喜欢本文的话,欢迎点赞和评论,写下你的见解。
如果想和我一起学习编程,不妨点个关注,我们一起学习,一同成长。
之后我还会输出更多高质量内容,欢迎收看。


发表评论