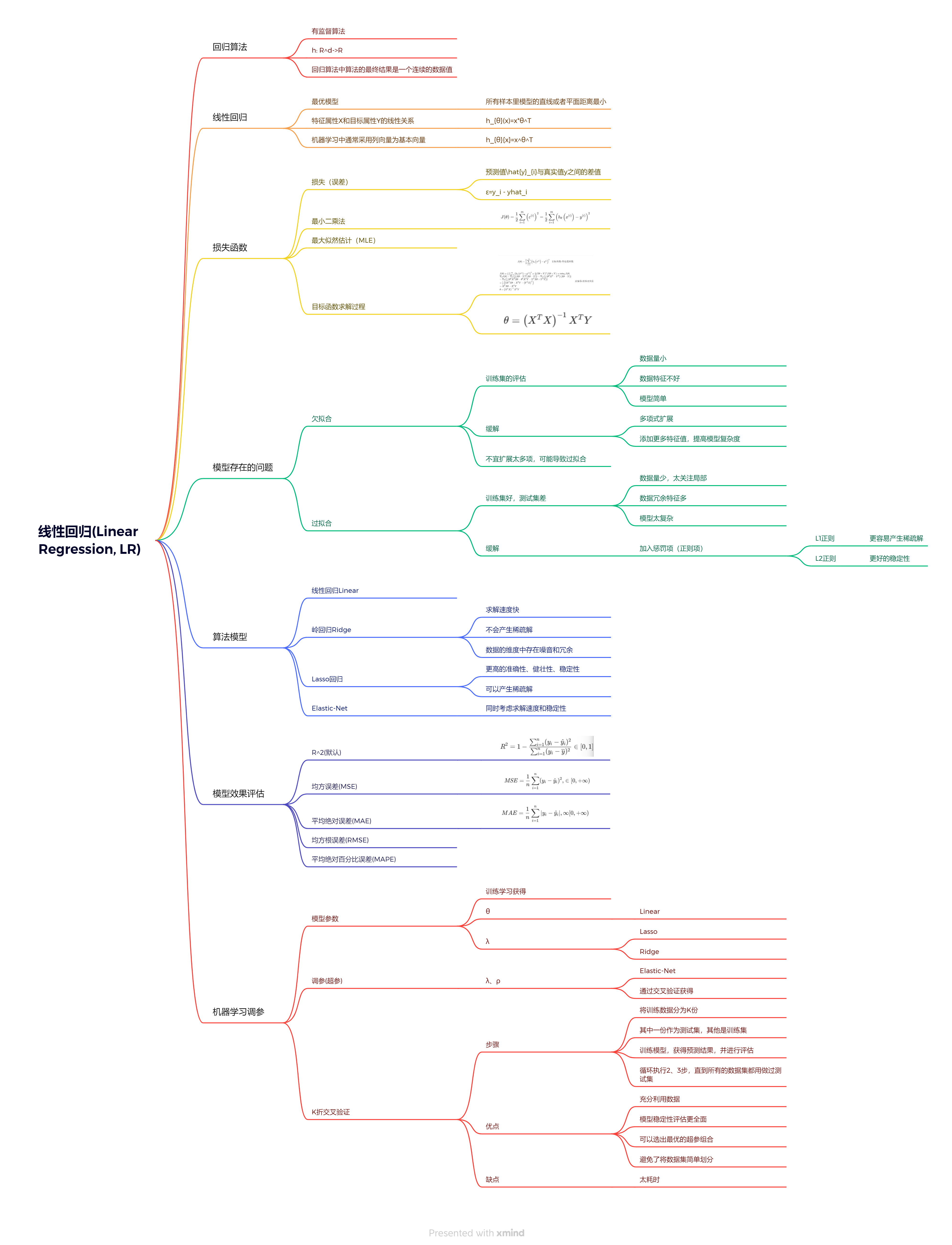
引入回归算法
什么是“回归”?
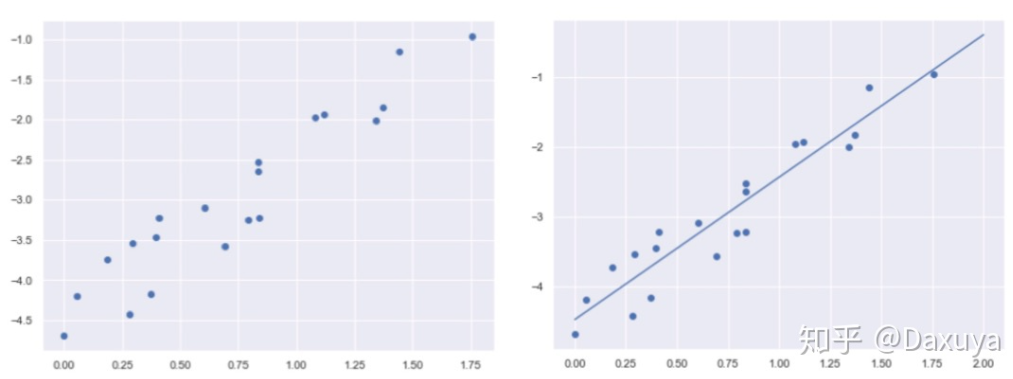
什么是“线性”?
什么是线性回归?
什么是回归算法
- 回归算法是一种有监督算法
- 建立“解释”变量(自变量x)和观测值(因变量y)之间的关系
- 从机器学习的角度来讲,用于构建一个算法模型(函数)来做属性(x)与标签(y)之间的映射关系,在算法的学习过程中,
试图寻找一个函数 h : r d − > r h: r^d->r h:rd−>r,使得参数之间的关系拟合性最好。
- 回归算法中算法(函数)的最终结果是一个连续的数据值,输入值(属性值)是一个d维度的属性/数值向量
线性回归
katex parse error: {split} can be used only in display mode.
损失函数
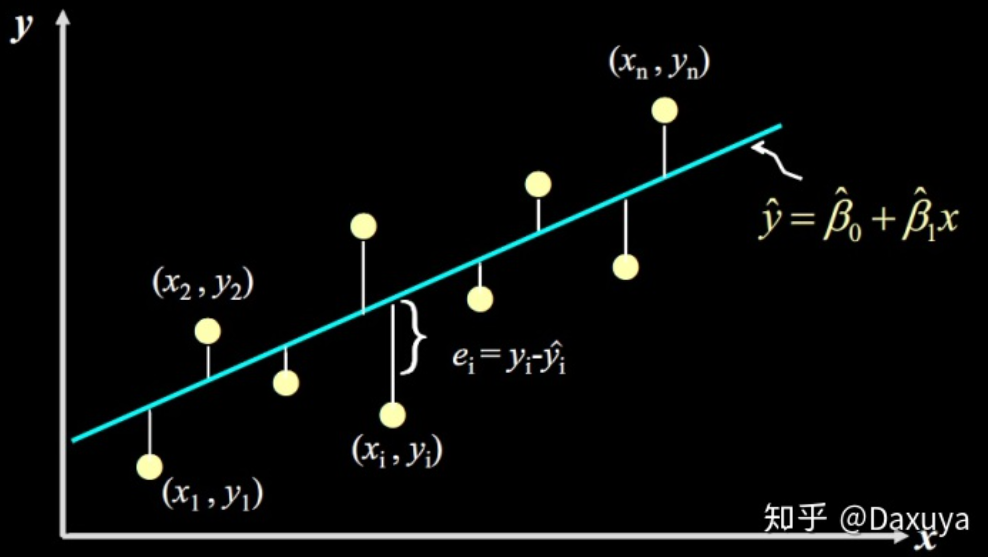
- 假设函数计算出的点 y i ^ \hat{y_i} yi^** 与真实数据点** y \text{y} y的间隔(差值)就是我们要找的点到直线的距离。机器学习里将这个差值叫误差,其表达式:
ε = y i − y ^ i \varepsilon=y_i-\hat{y}_i ε=yi−y^i
∑ ε 2 = ∑ ( y − y ^ i ) 2 = ∑ ( y − w 0 − w 1 x ) 2 \sum\varepsilon^2=\sum(y-\hat y_i)^2=\sum(y-w_0-w_1x)^2 ∑ε2=∑(y−y^i)2=∑(y−w0−w1x)2
- 在机器学习中,人们也称误差为损失,所以这种求误差的方法也可以说是求损失的方法。而sse也就是线性回归中最常用的损失函数了
最小二乘法
katex parse error: {align} can be used only in display mode.
最大似然估计
正态分布
- 理想误差 ε ( i ) ( 1 ≤ i ≤ n ) \varepsilon^{(\mathrm{i})}(1 \leq i \leq n) ε(i)(1≤i≤n),独立同分布的,服从均值为0,方差为某 θ 2 \theta^2 θ2定值的高斯分布(就是正态分布)
- 随机现象可以看做众多因素的独立影响的综合反应,往往服从正态分布,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。误差出现的概率:
katex parse error: {align} can be used only in display mode.
- **原因:**中心极限定理,解释了为什么服从正态分布

似然函数
katex parse error: {align} can be used only in display mode.
katex parse error: {align} can be used only in display mode.
katex parse error: {align} can be used only in display mode.
katex parse error: {align} can be used only in display mode.\thetakatex parse error: expected 'eof', got '}' at position 17: …的似然估计-联合概率-似然函数}̲\\ \end{align}
似然函数取对数
katex parse error: {align} can be used only in display mode.
据此,我们求合适的直线问题就转化为了,极大化似然函数转化求 j ( θ ) j(\theta) j(θ)的最小值,即求出 θ \theta θ的最优解
目标函数的求解过程
katex parse error: {align} can be used only in display mode.
katex parse error: {align} can be used only in display mode.
据此得到: θ = ( x t x ) − 1 x t y \theta=\left(x^tx\right)^{-1}x^ty θ=(xtx)−1xty,下面我们来分析这个式子
(解决欠拟合)多项式扩展
将任意向量x的
l
p
l_{p}
lp范数的定义:
∣
∣
x
∣
∣
p
=
∑
i
∣
x
i
∣
p
p
||x||_{p}=\sqrt[p]{\sum_{i}|x_{i}|^p}
∣∣x∣∣p=p∑i∣xi∣p
(解决过拟合)岭回归(ridge regression)算法和lasso算法
目标函数加入惩罚项的损失函数:
katex parse error: {align} can be used only in display mode.
ridge(l2-norm)(岭回归):
lasso(l1-norm):
elastic net(l1 & l2-norm)
模型效果评估
在回归任务(对连续值的预测)中,常见的评估指标(metric)有:平均绝对误差(mean absolute error,mae)、均方误差(mean square error,mse)、均方根误差(root mean square error,rmse)和平均绝对百分比误差(mean absolute percentage error,mape),其中用得最为广泛的就是mae和mse
机器学习调参
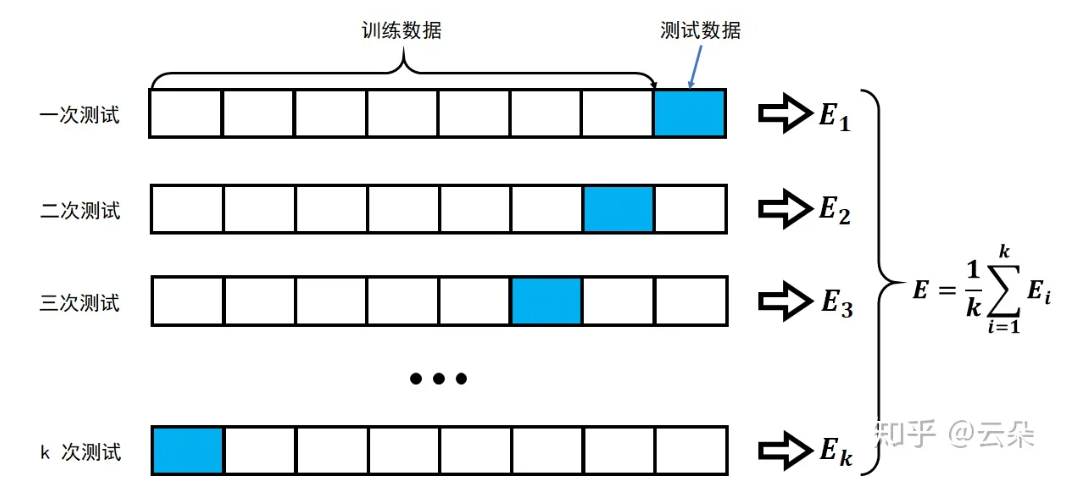
- k折交叉验证:将训练数据分为多份,其中一份进行数据验证并获取最优的超参:λ和p训练(返回训练)-验证8000(分5等分)-测试(最后)
- 多则交叉验证可以获得多组,更稳定,进行求均值,比如:十折交叉验证、五折交叉验证(scikit-learn中默认)等;





发表评论