glmnet是一个通过惩罚最大似然关系拟合广义线性模型的软件包。正则化路径是针对正则化参数λ的值网格处的lasso或elastic net(弹性网络)惩罚值计算的。
最近我们被客户要求撰写关于lasso的研究报告,包括一些图形和统计输出。该算法非常快,并且可以利用输入矩阵中的稀疏性 x。它适合线性,逻辑和多项式,泊松和cox回归模型。可以从拟合模型中做出各种预测。它也可以拟合多元线性回归。
视频:lasso回归、岭回归等正则化回归数学原理及r语言实例
lasso回归、岭回归等正则化回归数学原理及r语言实例
glmnet 解决以下问题

在覆盖整个范围的λ值网格上。这里l(y,η)是观察i的负对数似然贡献;例如对于高斯分布是![]() 。 弹性网络惩罚由α控制,lasso(α= 1,默认),ridge(α= 0)。调整参数λ控制惩罚的总强度。
。 弹性网络惩罚由α控制,lasso(α= 1,默认),ridge(α= 0)。调整参数λ控制惩罚的总强度。
众所周知,岭惩罚使相关预测因子的系数彼此缩小,而套索倾向于选择其中一个而丢弃其他预测因子。弹性网络则将这两者混合在一起。
glmnet 算法使用循环坐标下降法,该方法在每个参数固定不变的情况下连续优化目标函数,并反复循环直到收敛,我们的算法可以非常快速地计算求解路径。
代码可以处理稀疏的输入矩阵格式,以及系数的范围约束,还包括用于预测和绘图的方法,以及执行k折交叉验证的功能。
快速开始
首先,我们加载 glmnet 包:
library(glmnet)包中使用的默认模型是高斯线性模型或“最小二乘”。我们加载一组预先创建的数据以进行说明。用户可以加载自己的数据,也可以使用工作空间中保存的数据。
该命令 从此保存的r数据中加载输入矩阵 x 和因向量 y。
我们拟合模型 glmnet。
fit = glmnet(x, y)可以通过执行plot 函数来可视化系数 :
plot(fit)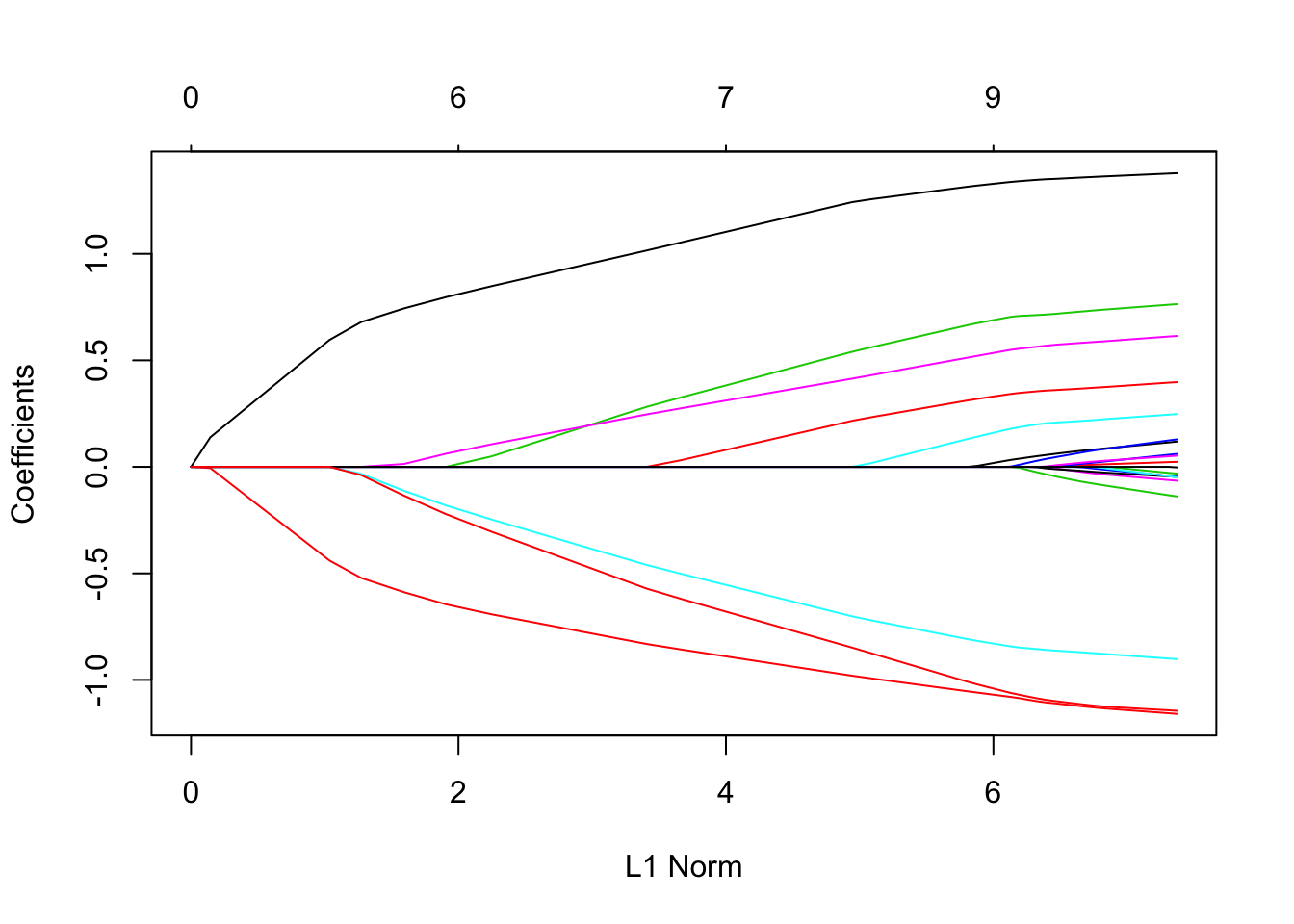
每条曲线对应一个变量。它显示了当λ变化时,其系数相对于整个系数向量的ℓ1范数的路径。上方的轴表示当前λ处非零系数的数量,这是套索的有效自由度(df)。用户可能还希望对曲线进行注释。这可以通过label = true 在plot命令中进行设置来完成 。
glmnet 如果我们只是输入对象名称或使用print 函数,则会显示每个步骤的路径 摘要 :
print(fit)##
## call: glmnet(x = x, y = y)
##
## df %dev lambda
## [1,] 0 0.0000 1.63000
## [2,] 2 0.0553 1.49000
## [3,] 2 0.1460 1.35000
## [4,] 2 0.2210 1.23000
## [5,] 2 0.2840 1.12000
## [6,] 2 0.3350 1.02000
## [7,] 4 0.3900 0.93300
## [8,] 5 0.4560 0.85000
## [9,] 5 0.5150 0.77500
## [10,] 6 0.5740 0.70600
## [11,] 6 0.6260 0.64300
## [12,] 6 0.6690 0.58600
## [13,] 6 0.7050 0.53400
## [14,] 6 0.7340 0.48700
## [15,] 7 0.7620 0.44300
## [16,] 7 0.7860 0.40400
## [17,] 7 0.8050 0.36800
## [18,] 7 0.8220 0.33500
## [19,] 7 0.8350 0.30600
## [20,] 7 0.8460 0.27800
它从左到右显示了非零系数的数量(df),解释的(零)偏差百分比(%dev)和λ(lambda)的值。
我们可以在序列范围内获得一个或多个λ处的实际系数:
coef(fit,s=0.1)## 21 x 1 sparse matrix of class "dgcmatrix"
## 1
## (intercept) 0.150928
## v1 1.320597
## v2 .
## v3 0.675110
## v4 .
## v5 -0.817412
## v6 0.521437
## v7 0.004829
## v8 0.319416
## v9 .
## v10 .
## v11 0.142499
## v12 .
## v13 .
## v14 -1.059979
## v15 .
## v16 .
## v17 .
## v18 .
## v19 .
## v20 -1.021874还可以使用新的输入数据在特定的λ处进行预测:
predict(fit,newx=nx,s=c(0.1,0.05))## 1 2
## [1,] 4.4641 4.7001
## [2,] 1.7509 1.8513
## [3,] 4.5207 4.6512
## [4,] -0.6184 -0.6764
## [5,] 1.7302 1.8451
## [6,] 0.3565 0.3512
## [7,] 0.2881 0.2662
## [8,] 2.7776 2.8209
## [9,] -3.7016 -3.7773
## [10,] 1.1546 1.1067该函数 glmnet 返回一系列模型供用户选择。交叉验证可能是该任务最简单,使用最广泛的方法。
cv.glmnet 是交叉验证的主要函数。
cv.glmnet 返回一个 cv.glmnet 对象,此处为“ cvfit”,其中包含交叉验证拟合的所有成分的列表。
我们可以绘制对象。
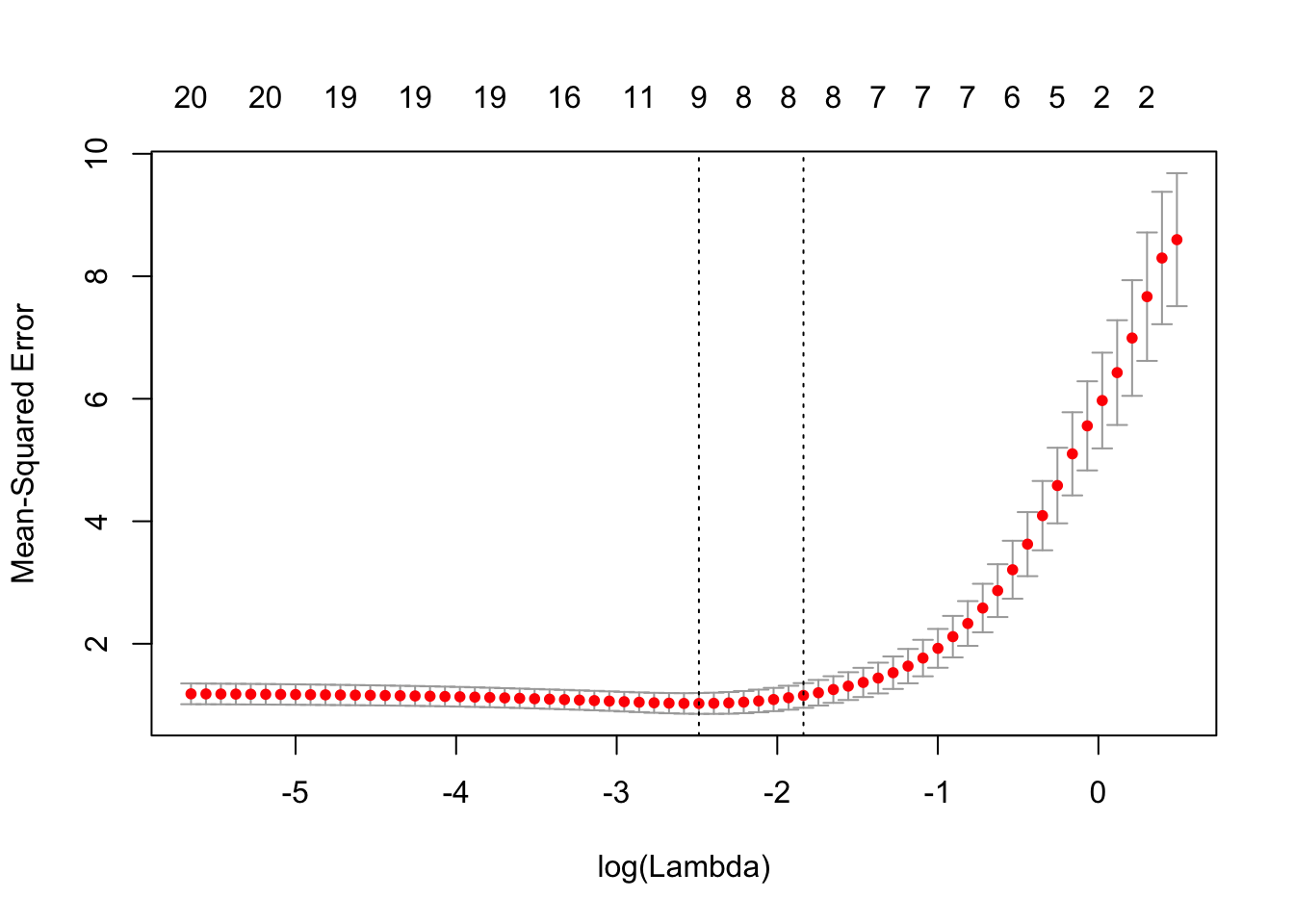
它包括交叉验证曲线(红色虚线)和沿λ序列的上下标准偏差曲线(误差线)。垂直虚线表示两个选定的λ。
我们可以查看所选的λ和相应的系数。例如,
cvfit$lambda.min## [1] 0.08307lambda.min 是给出最小平均交叉验证误差的λ值。保存的另一个λ是 lambda.1se,它给出了的模型,使得误差在最小值的一个标准误差以内。我们只需要更换 lambda.min 到lambda.1se 以上。
coef(cvfit, s = "lambda.min")## 21 x 1 sparse matrix of class "dgcmatrix"
## 1
## (intercept) 0.14936
## v1 1.32975
## v2 .
## v3 0.69096
## v4 .
## v5 -0.83123
## v6 0.53670
## v7 0.02005
## v8 0.33194
## v9 .
## v10 .
## v11 0.16239
## v12 .
## v13 .
## v14 -1.07081
## v15 .
## v16 .
## v17 .
## v18 .
## v19 .
## v20 -1.04341注意,系数以稀疏矩阵格式表示。原因是沿着正则化路径的解通常是稀疏的,因此使用稀疏格式在时间和空间上更为有效。
可以根据拟合的cv.glmnet 对象进行预测 。让我们看一个示例。
## 1
## [1,] -1.3647
## [2,] 2.5686
## [3,] 0.5706
## [4,] 1.9682
## [5,] 1.4964newx


发表评论