基于蜣螂算法优化的lssvm回归预测 - 附代码
摘要:为了提高最小二乘支持向量机(lssvm)的回归预测准确率,对lssvm中的惩罚参数和核惩罚参数利用蜣螂算法进行优化。
1.数据集
数据信息如下:
data.mat 的中包含input数据和output数据
其中input数据维度为:2000*2
其中output数据维度为2000*1
所以rf模型的数据输入维度为2;输出维度为1。
2.lssvm模型
lssvm请自行参考相关机器学习书籍。
3.基于蜣螂算法优化的lssvm
蜣螂算法的具体原理参考博客:。
蜣螂算法的优化参数为惩罚参数和核惩罚参数。适应度函数为rf对训练集和测试集的均方误差(mse),均方误差mse越低越好。
f
i
n
t
e
n
e
s
s
=
m
s
e
[
p
r
e
d
i
c
t
(
t
r
a
i
n
)
]
+
m
s
e
[
p
r
e
d
i
c
t
(
t
e
s
t
)
]
finteness = mse[predict(train)] + mse[predict(test)]
finteness=mse[predict(train)]+mse[predict(test)]
4.测试结果
数据划分信息如下: 训练集数量为1900组,测试集数量为100组
蜣螂参数设置如下:
%% 利用蜣螂算法选择回归预测分析最佳的lsssvm参数c&g
%% 蜣螂参数设置
% 定义优化参数的个数,在该场景中,优化参数的个数dim为2 。
% 定义优化参数的上下限,如c的范围是[0.01, 1], g的范围是[2^-5, 2^5],那么参数的下限lb=[0.01, 2^-5];参数的上限ub=[1, 2^5]。
%目标函数
fobj = @(x) fun(x,pn_train,tn_train,pn_test,tn_test);
% 优化参数的个数 (c、g)
dim = 2;
% 优化参数的取值下限
lb = [0.01,0.01];
ub = [5,5];
% 参数设置
pop =20; %蜣螂数量
max_iteration=5;%最大迭代次数
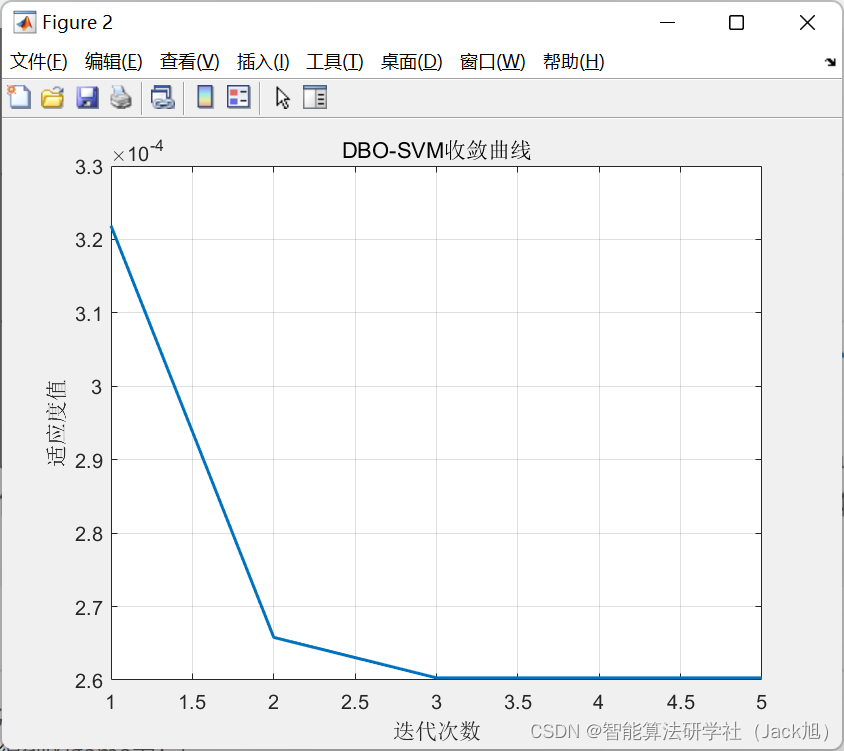

dbo-lssvm优化得到的最优参数为:
dbo-lssvm优化得到的gama为:5
dbo-lssvm优化得到的sig2为:0.24957
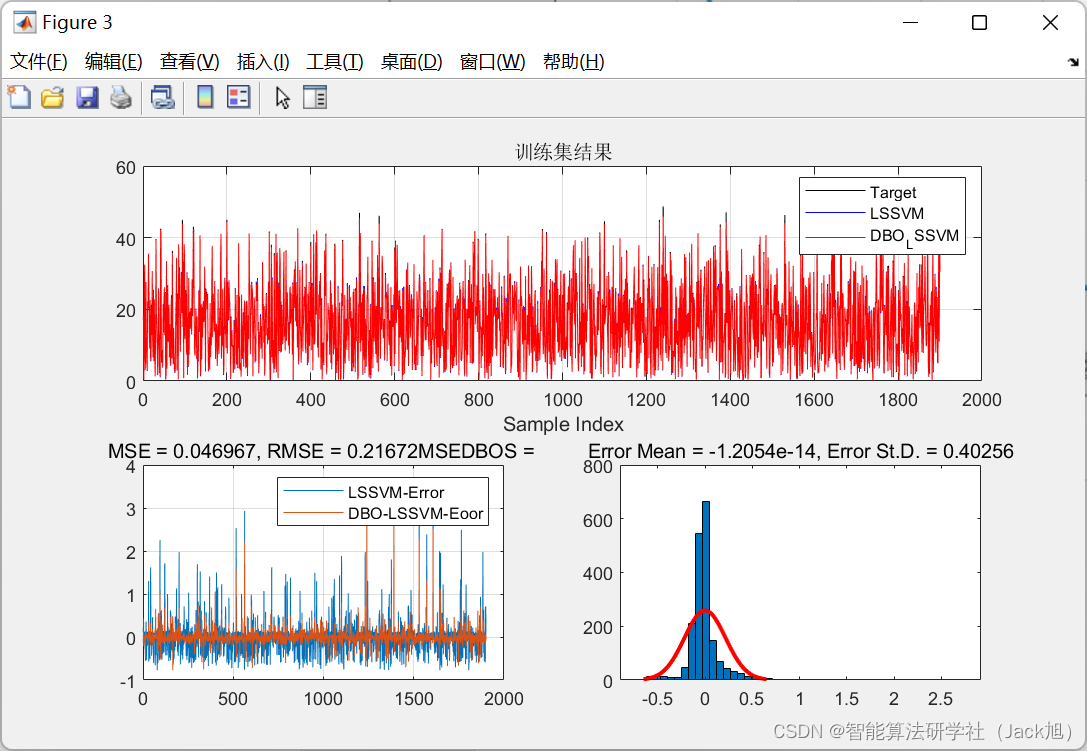
dbo-lssvm结果:
dbo-lssvm训练集mse:0.046967
dbo-lssvm测试集mse:0.10745
lssvm结果:
lssvm训练集mse:0.16197
lssvm测试集mse:0.32174
从mse结果来看,经过改进后的蜣螂-lssvm明显优于未改进前的结果。


发表评论