基础概念
分类问题与回归问题
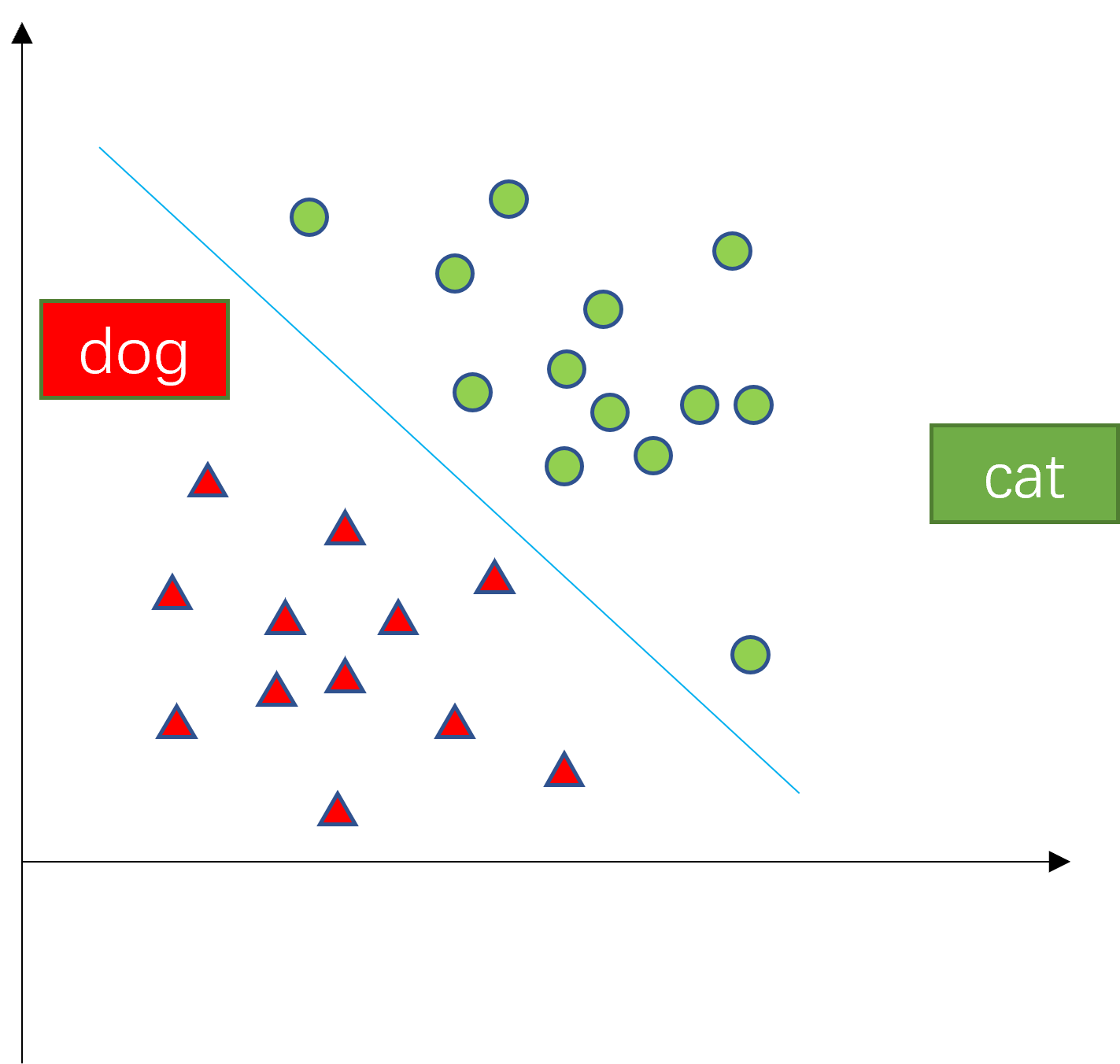
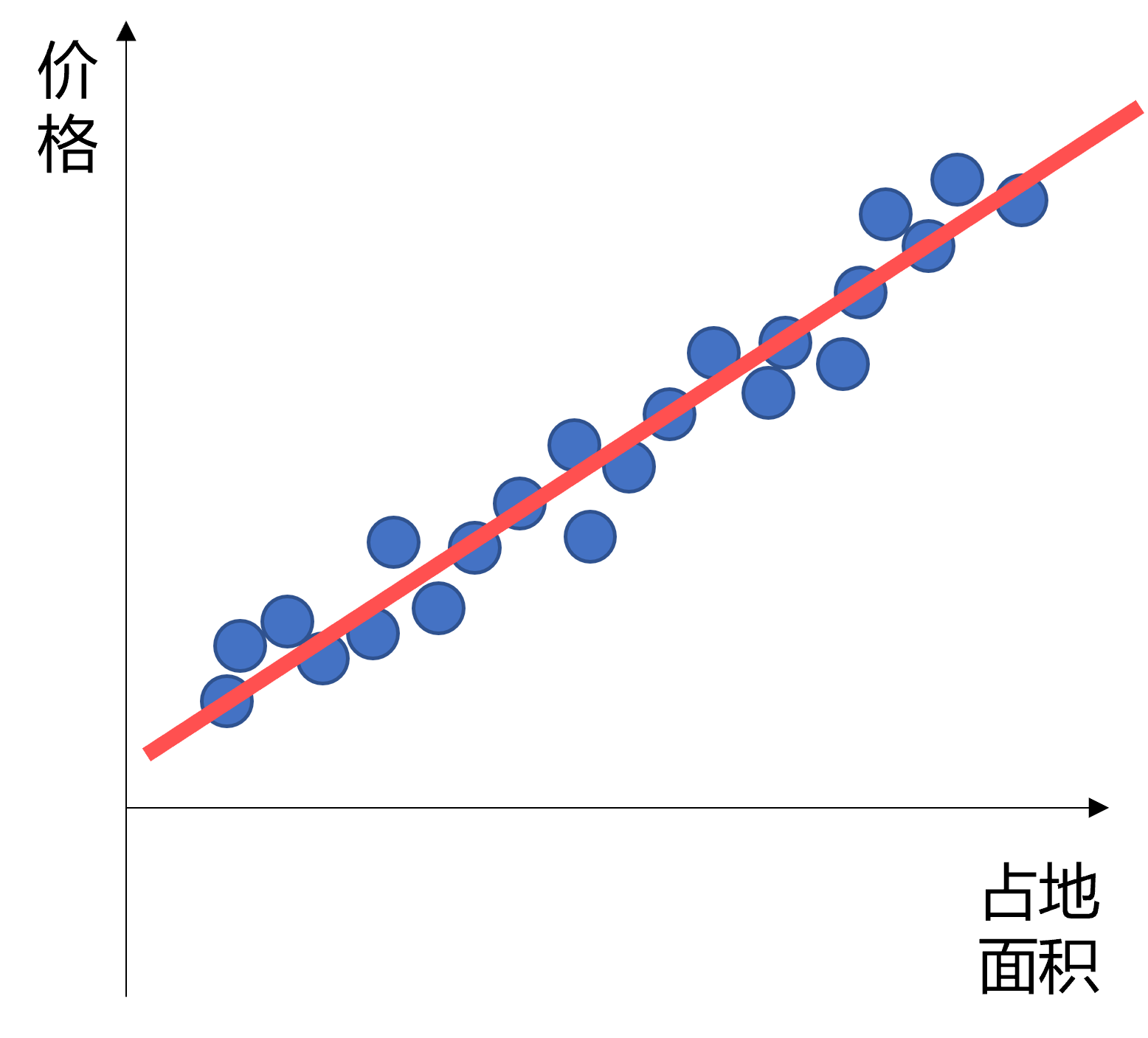
sigmoid函数
从图像上看,对于 logistic 函数而言,x = 0 是一个有着特殊意义坐标,越靠近 0 和越远离 0 会出现两种截然不同的情况:任何y > 0.5 的数据可以划分到 “1”类中;而y < 0.5 的数据可以划分到 “0”类。因此可以把 logistic 看做解决二分类问题的分类器。如果想要 logistic 分类器预测准确,那么 x 的取值距离 0 越远越好,这样结果值才能无限逼近于 0 或者 1。
接下来通过两幅图像来解释为什么需要让x离0越远越好。
将sigmoid图像x的取值缩小范围至[-0.6 , 0.6]可获得如下的图像:
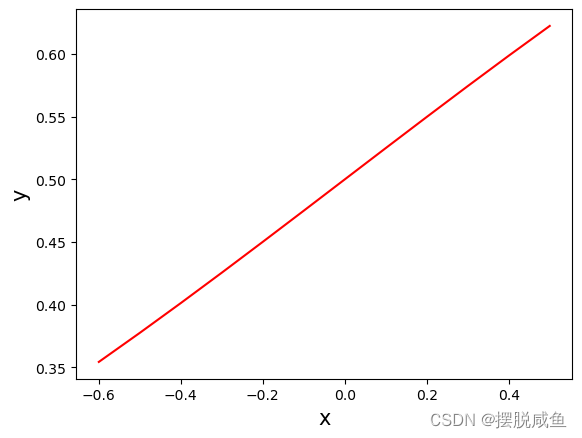
将sigmoid的x取值扩大范围至[-60, 60]可以获得如下图像:
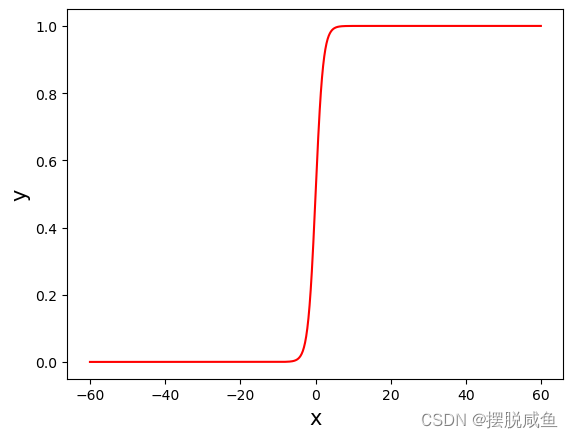
通过对比两幅图像,我们可以发现,当x取值比较小时,sigmoid函数与线性模型无异;当x取值大起来,我们发现sigmoid函数呈现的是一个阶梯式图像,这对我们的二分类来说简直不要太妙。这也就是为什么要采用logistic进行二分类的原因。
基于最优化方法的最佳回归系数确定
问题引出
通过上面的描述,我们发现,为了实现logistic回归分类,我们可以在每一个特征上乘以一个回归系数,然后把相乘的结果累加,代入sigmoid函数中就可以得到一个在[ 0,1 ]范围的值y,我们就可以通过判别y的值来实现分类。(例:y > 0.5为1类,y < 0.5为0类 )
公式描述:
z = w t x + b z =\mathbf{ w^{t}x} +b z=wtx+b
y = 1 1 + e − z y = \frac{1}{1+e^{-z} } y=1+e−z1
带入z可得:
y = 1 1 + e w t x + b y = \frac{1}{1+e^{\mathbf{ w^{t}x} +b} } y=1+ewtx+b1
由上式可以做出以下假设
由于y的函数有分式和指数e的,所以我们采用对数函数对其进行一种映射:
ln y 1 − y = ln p ( y = 1 ∣ x ) p ( y = 0 ∣ x ) = w t x + b \ln_{}{\frac{y}{1-y} } = \ln_{}{\frac{p(y=1|x)}{p(y=0|x)} }=\mathbf{ w^{t}x} +b ln1−yy=lnp(y=0∣x)p(y=1∣x)=wtx+b
p ( y = 1 ∣ x ) = w t x + b 1 + w t x + b p(y=1|x)=\frac{\mathbf{ w^{t}x} +b}{1+\mathbf{ w^{t}x} +b} p(y=1∣x)=1+wtx+bwtx+b
p ( y = 0 ∣ x ) = 1 1 + w t x + b p(y=0|x)=\frac{1}{1+\mathbf{ w^{t}x} +b} p(y=0∣x)=1+


发表评论