c#代码计算数学表达式
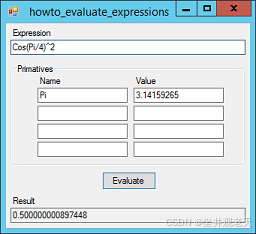
此程序展示了如何使用 c# 代码来计算数学表达式。
该程序以 以下代码开始。
此代码声明了一个dictionary,稍后将使用它来保存变量。(例如,如果用户想要 a = 10、b = 3 和 pi = 3.14159265。)
然后它定义了一个precedence枚举来表示运算符的优先级。例如,乘法的优先级高于加法。
单击“evaluate”按钮时,程序会复制您输入到“ primatives dictionary”中的任何基元,然后调用evaluateexpression方法,该方法会执行所有有趣的工作。
该方法很长,因此我将分段描述
// stores user-entered primitives like x = 10.
private dictionary<string, string> primatives;
private enum precedence
{
none = 11,
unary = 10, // not actually used.
power = 9, // we use ^ to mean exponentiation.
times = 8,
div = 7,
modulus = 6,
plus = 5,
}// evaluate the expression.
private double evaluateexpression(string expression)
{
int best_pos = 0;
int parens = 0;
// remove all spaces.
string expr = expression.replace(" ", "");
int expr_len = expr.length;
if (expr_len == 0) return 0;
// if we find + or - now, then it's a unary operator.
bool is_unary = true;
// so far we have nothing.
precedence best_prec = precedence.none;
// find the operator with the lowest precedence.
// look for places where there are no open
// parentheses.
for (int pos = 0; pos < expr_len; pos++)
{
// examine the next character.
string ch = expr.substring(pos, 1);
// assume we will not find an operator. in
// that case, the next operator will not
// be unary.
bool next_unary = false;
if (ch == " ")
{
// just skip spaces. we keep them here
// to make the error messages easier to
}
else if (ch == "(")
{
// increase the open parentheses count.
parens += 1;
// a + or - after "(" is unary.
next_unary = true;
}
else if (ch == ")")
{
// decrease the open parentheses count.
parens -= 1;
// an operator after ")" is not unary.
next_unary = false;
// if parens < 0, too many )'s.
if (parens < 0)
throw new formatexception(
"too many close parentheses in '" +
expression + "'");
}
else if (parens == 0)
{
// see if this is an operator.
if ((ch == "^") || (ch == "*") ||
(ch == "/") || (ch == "\\") ||
(ch == "%") || (ch == "+") ||
(ch == "-"))
{
// an operator after an operator
// is unary.
next_unary = true;
// see if this operator has higher
// precedence than the current one.
switch (ch)
{
case "^":
if (best_prec >= precedence.power)
{
best_prec = precedence.power;
best_pos = pos;
}
break;
case "*":
case "/":
if (best_prec >= precedence.times)
{
best_prec = precedence.times;
best_pos = pos;
}
break;
case "%":
if (best_prec >= precedence.modulus)
{
best_prec = precedence.modulus;
best_pos = pos;
}
break;
case "+":
case "-":
// ignore unary operators
// for now.
if ((!is_unary) &&
best_prec >= precedence.plus)
{
best_prec = precedence.plus;
best_pos = pos;
}
break;
} // end switch (ch)
} // end if this is an operator.
} // else if (parens == 0)
is_unary = next_unary;
} // for (int pos = 0; pos < expr_len; pos++)该方法的这一部分用于查找表达式中优先级最低的运算符。为此,它只需循环遍历表达式,检查其运算符字符,并确定它们的优先级是否低于先前找到的运算符。
下面的代码片段显示了下一步
// if the parentheses count is not zero,
// there's a ) missing.
if (parens != 0)
{
throw new formatexception(
"missing close parenthesis in '" +
expression + "'");
}
// hopefully we have the operator.
if (best_prec < precedence.none)
{
string lexpr = expr.substring(0, best_pos);
string rexpr = expr.substring(best_pos + 1);
switch (expr.substring(best_pos, 1))
{
case "^":
return math.pow(
evaluateexpression(lexpr),
evaluateexpression(rexpr));
case "*":
return
evaluateexpression(lexpr) *
evaluateexpression(rexpr);
case "/":
return
evaluateexpression(lexpr) /
evaluateexpression(rexpr);
case "%":
return
evaluateexpression(lexpr) %
evaluateexpression(rexpr);
case "+":
return
evaluateexpression(lexpr) +
evaluateexpression(rexpr);
case "-":
return
evaluateexpression(lexpr) -
evaluateexpression(rexpr);
}
}如果括号未闭合,该方法将引发异常。否则,它会使用优先级最低的运算符作为分界点,将表达式拆分成多个部分。然后,它会递归调用自身来评估子表达式,并使用适当的操作来合并结果。
例如,假设表达式为 2 * 3 + 4 * 5。那么优先级最低的运算符是 +。该函数将表达式分解为 2 * 3 和 4 * 5,并递归调用自身来计算这些子表达式的值(得到 6 和 20),然后使用加法将结果合并(得到 26)。
以下代码显示该方法如何处理函数调用
// if we do not yet have an operator, there
// are several possibilities:
//
// 1. expr is (expr2) for some expr2.
// 2. expr is -expr2 or +expr2 for some expr2.
// 3. expr is fun(expr2) for a function fun.
// 4. expr is a primitive.
// 5. it's a literal like "3.14159".
// look for (expr2).
if (expr.startswith("(") & expr.endswith(")"))
{
// remove the parentheses.
return evaluateexpression(expr.substring(1, expr_len - 2));
}
// look for -expr2.
if (expr.startswith("-"))
{
return -evaluateexpression(expr.substring(1));
}
// look for +expr2.
if (expr.startswith("+"))
{
return evaluateexpression(expr.substring(1));
}
// look for fun(expr2).
if (expr_len > 5 & expr.endswith(")"))
{
// find the first (.
int paren_pos = expr.indexof("(");
if (paren_pos > 0)
{
// see what the function is.
string lexpr = expr.substring(0, paren_pos);
string rexpr = expr.substring(paren_pos + 1,
expr_len - paren_pos - 2);
switch (lexpr.tolower())
{
case "sin":
return math.sin(evaluateexpression(rexpr));
case "cos":
return math.cos(evaluateexpression(rexpr));
case "tan":
return math.tan(evaluateexpression(rexpr));
case "sqrt":
return math.sqrt(evaluateexpression(rexpr));
case "factorial":
return factorial(evaluateexpression(rexpr));
// add other functions (including
// program-defined functions) here.
}
}
}此代码检查表达式是否以 ( 开头并以 结尾。如果是,则删除这些括号并计算表达式的其余部分。
接下来,代码确定表达式是否以一元 + 或 - 运算符开头。如果是,程序将计算不带运算符的表达式,如果运算符为 -,则对结果取反。
然后,代码会查找sin、cos和factorial等函数。如果找到,它会调用该函数并返回结果。(下载示例以查看factorial函数。)您可以类似地添加其他函数。
以下代码显示了该方法的其余部分
// see if it's a primitive.
if (primatives.containskey(expr))
{
// return the corresponding value,
// converted into a double.
try
{
// try to convert the expression into a value.
return double.parse(primatives[expr]);
}
catch (exception)
{
throw new formatexception(
"primative '" + expr +
"' has value '" +
primatives[expr] +
"' which is not a double.");
}
}
// it must be a literal like "2.71828".
try
{
// try to convert the expression into a double.
return double.parse(expr);
}
catch (exception)
{
throw new formatexception(
"error evaluating '" + expression +
"' as a constant.");
}
}如果表达式仍未求值,则它必须是您在文本框中输入的原始值或数值。
代码将检查原始字典以查看表达式是否存在。
如果值在字典中,则代码获取其值,将其转换为双精度值,然后返回结果。
总结
以上为个人经验,希望能给大家一个参考,也希望大家多多支持代码网。




发表评论