蛮力排序:冒泡、插入、选择排序
冒泡排序:最好请阔下比较n-1次,移动0此,时间复杂度为o(n);最坏情况下比较n(n-1)/2次,移动3n(n-1)/2次,时间复杂度为o(n^2)
平均时间复杂度为o(n^2)
算法的稳定性:
具有相同关键字的元素在排序时相对次序不发生改变的算法,具有稳定性。
对于冒泡算法,交换语句如下:
if(list[j-1] > list[j])
{
swap(list[j-1],list[j])
flag := true;
}
交换条件中不含等号,故该算法具有稳定性。
插入排序
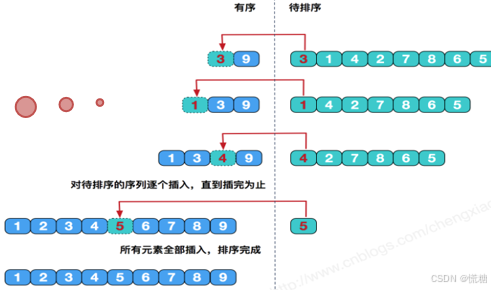
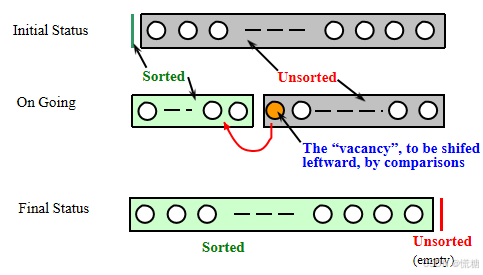
最好需要n-1次比较,2(n-1)次移动,时间复杂度为o(n)
最坏情况需要(n+1)(n-1)/2次比较,(n-1)(n+4)/2次移动,时间复杂度为o(n^2)
选择排序
基本思想:每一趟从待排序列选出最小(或最大)的一个元素,顺序放在已排好序的数列最后,直到所有待排元素都完成排序
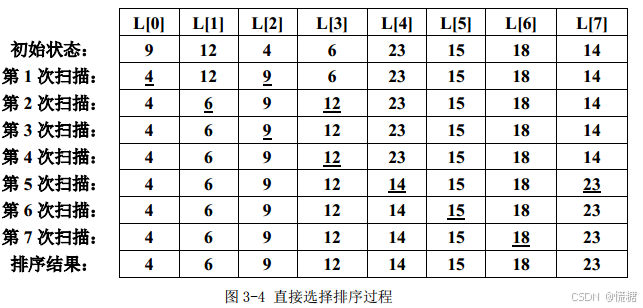
直接选择排序是对冒泡排序算法的一种改进,可以减少移动次数。算法时间复杂度为o(n^2)
分治排序算法
树形选择排序步骤:
1.将记录进行两两分组,讲每组的最小值或者最大值设置为这组的父节点,逐层比较得到最值作为输出;
2.讲最为最值输出的值设置为无穷大,从被最小元素打败的节点显出次值,作为输出
3.循环2
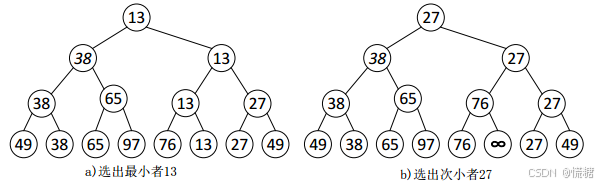
树形选择排序实质上是一个构建完全二叉树的过程,含有n个叶子节点的完全二叉树深度为(log2n)+1,因此时间复杂度就是这个。
与直接选择排序相比,树形选择排序减少了比较次数,降低了时间复杂度,但是需要的辅助存储空间较多,并且需要进行多余比较。
快速排序是一种典型的基于分治模式的排序算法,它通过选择基准元素来实现问题的分解
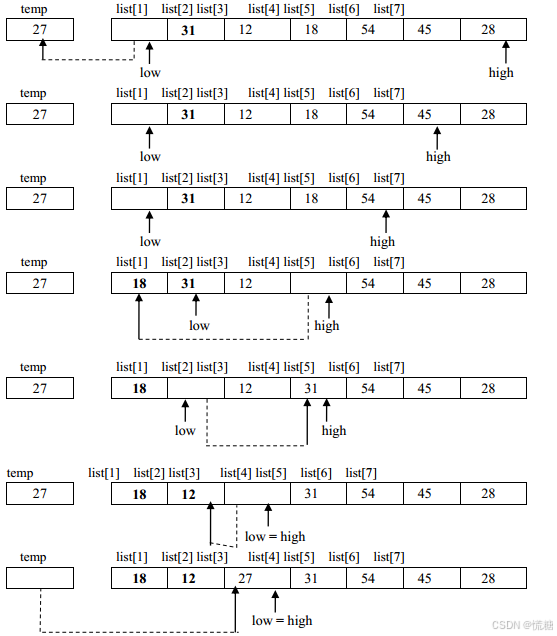
选定主元27,将序列中小于27的元素放到其左边,大于27的元素放到其右边,这便是一次划分操作
快速排序的性能受到划分过程的影响。子序列划分的越不均衡,排序的性能越差
最坏情况下,每次划分的两个子序列中都有一个长度为1,此时快速排序的时间复杂度为o(n2)
在平均情况下,我们可以假设每次划分的结果都是均匀的,此时快速排序的时间复杂度满足递归式: t(n)=2t(n/2)+o(n)
根据master定理,可知t(n)=o(nlogn)
归并排序使用的是“易分难和”的策略:归并排序一般分为分解和合并两部分,我们将序列分解为两个小的子序列。当子序列排序完成后,再将它们合并成一个有序序列
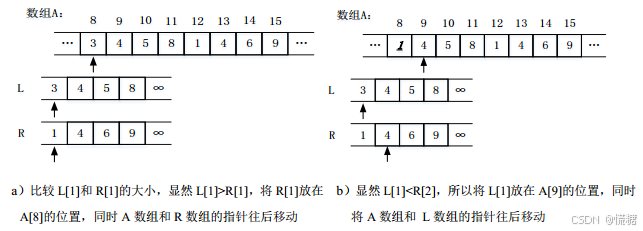
更新完后,数组a中第8,9个位置的值分别为1,3。直至数组l,r中的元素均已比较完,算法结束
归并排序时间复杂度归并排序算法排序n个元素的递归方程为:m(n)=2m(n/2)+n
由master定理推导出时间复杂度为o(nlog n)
堆排序
本质上而言,堆是一棵满足一定条件的完全二叉树
对小根堆而言,结点的所有后代相关的数据都大于该结点上的数据;对于大根堆而言,结点的所有后代相关数据都小于该结点上的数据;
二叉树左右孩子之间没有绝对的大小关系;
堆的任意一棵子树也是堆。
完全二叉树-> 每个节点最多只有两个子节点
树最下面的两层结点的度小于2,最下面⼀层的结点都集中在该层最左边的若干位置
堆排序算法:
以序列的降序排列为例,根据堆的性质可知我们可以通过不断建立大根堆然后输出根节点来实现排序。
当我们输出一个根结点之后将其从堆中剔除,将剩下的结点重建成大根堆再输出根结点。当所有结点输出完成,我们就完成了对序列的降序排序。
升序排序可以通过构造小根堆来实现
线性时间排序
线性时间算法的思想是不通过比较操作来确定元素的次序,但这样会增加空间复杂度
计数排序
对于已知数据范围的非负整数序列l,计数排序的基本思想是通过计算序列中元素出现的次数来确定元素位置

计数排序的时间复杂度为o(n+k),其中n为待排元素个数,k为待排元素最大值加1。由于计数排序不需要比较操作,所以时间复杂度突破了o(nlogn)。
计数排序需要两个大小为n,一个大小为k的数组作为辅助存储器。
可以看出计数排序牺牲了空间复杂度换取时间复杂度
当o(k)>o(n*log(n))的时候其效率反而不如基于比较的排序
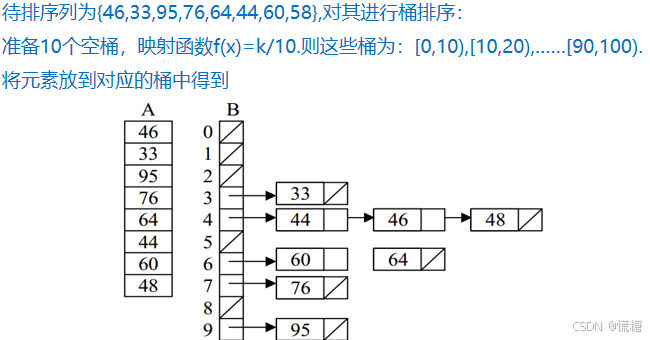
桶排序的基本思想是将待排元素分配到容量较小的有序区间单元中,这些有序区间单元称为桶。
由于桶中元素一般较少,所以桶内排序问题很容易计算。但桶排序需要大量的辅助存储空间,而且元素不能为负
桶排序的时间复杂度与各桶中元素个数是否均匀有关,对n个待排元素、m个桶,排序的平均时间复杂度为
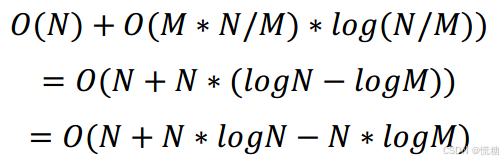
基数排序先把待排序列元素统一成同样的位数长度,然后将数据按位分开,从数据的最低有效位到最高有效位进行排序,从而得到有序序列。各个位进行排序的算法必须是稳定的
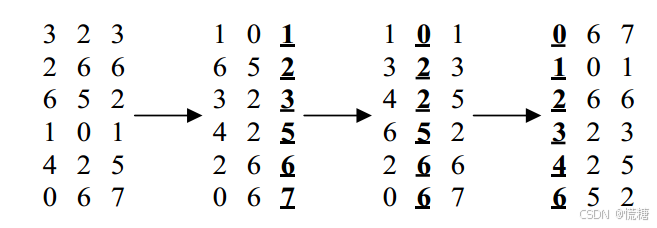
基数排序的时间复杂度与选取的对每个位进行排序的算法有关。
例如选用计数排序对各个位进行排序,共有d位,每一位有k种可能的取值,则该基数排序的时间复杂度为o(dn+dk)
归约是指为解决某一问题而设计的算法正好可以解决另外一个问题
为什么要进行排序归约?
在很多复杂问题当中,如果将其中的数据进行适当排序,将使得问题的求解变得简单。
寻找不重复的元素
最大间隙问题
合并果子数问题
最优树构造问题




发表评论