题目
【题目描述】
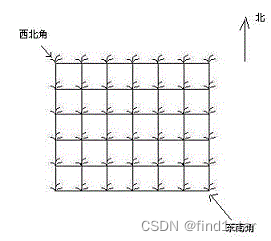
hello kitty想摘点花生送给她喜欢的米老鼠。她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。hello kitty只能向东或向南走,不能向西或向北走。问hello kitty最多能够摘到多少颗花生
分析
不能从当前点 去找下一个最优点 (贪心思想 当前局部最优解 不能代表全局最优解),后面未知路径可能有很大的数值,当前的选择对最终结果产生了影响
思路:去找当前最优点是由之前那个最优点传递并得到的,将全局最优解拆分为无数个局部最优解后统一取最优解
由题知hello kitty只能向东或向南走,不能向西或向北走。所以可以从起始点位的周边点开始,计算该周边点位经过最优路线所能得到的最多花生数量 :
该点花生数量+=max(该点上方花生数量,该点左方花生数量)。
array[i][j]+=max(array[i-1][j],array[i][j-1]);
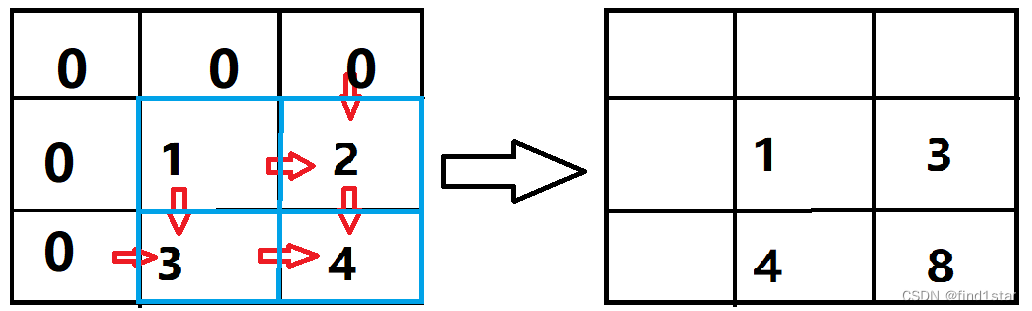
注意:该数组空出了0行与0列,避免了数组的越界问题
如图所示建立两个数组,一个数组存储花生田模型以及各点花生数量,另一个数组存储由第一个数组推算出来的各点最优总花生数量,则第二个数组的右下角即为最多花生数量。
改进1
原始花生数据不需要保存利用,第二步所以存储花生数量的数组,可直接使用第一步原数组进行数据替换

题目拓展
在原题目基础上,需要求出摘得花生最多的路径
拓展分析
路径依旧不能从当前点选择下一个位置应该选哪条路径,那么已知最后的终点就是最大花生数量,我们可以反推该点是由哪个上层顶点传递过来的,随后回退到上一个路径,接着重复寻找该上层顶点是由哪个上上层顶点传递过来的,直到推回至原点,记录该逆推路径,反向输出即为摘花生原始路径。
最优路径是由终点向前推,寻找每一个最大花生数顶点叠加而成,且反推路径只能向西或向北走,不能向东或向南走
所以:在从终点开始计算
该点左侧花生数量 > 该点上侧花生数量 : 路径从左侧来
该点左侧花生数量 <= 该点上侧花生数量 : 路径从上侧来
而且: 该点花生数量 - 上层路径花生数量 = 该点花生数量(路径标识)
改进2
由于最后创建的路径数组只是为了存储花生路径并倒叙输出,所以改用递归方式倒叙输出路径,略去路径数组。
题解代码
// 不能从当前点 去找下一个最优点 (贪心思想 当前局部最优解 不能代表全局最优解)
#include<bits/stdc++.h>
using namespace std;
int maxarray[100][100]; // 设置上限数组
int way[200]; // 设置路径数组
void recursion(int begin , int end ,int x,int y,int maxarray[100][100]); // 声明前置函数
int main() {
int row , column ; // 建图 row 行 column 列
cout<<"输入行数,列数\n";
cin>>row>>column;
// 一、得到花生分布数组与最大花生数量
// 1、初始化花生田数组
for(int i = 1 ; i <= row ; i++) {
for(int j = 1 ; j <= column ; j++) {
cout<<"输入maxarray["<<i<<"]["<<j<<"]\n";
cin>>maxarray[i][j];
}
}
cout<<"\n\n";
// 展示花生田
for(int i = 0 ; i <=row ; i++){
for(int j = 0 ; j <=column ; j++){
cout<<"\t"<<maxarray[i][j];
}
cout<<"\n";
}
cout<<"\n\n";
// 2、计算每个位置的叠加花生数量
for(int i = 1 ; i <= row ; i++) {
for(int j = 1 ; j <= column ; j++) {
//当前位置+【上面】或【左面】 = 从起始位置到该点花生最大值
maxarray[i][j]+=max(maxarray[i-1][j],maxarray[i][j-1]);
}
}
// 此时数组右下角为 maxarray[row][column] 即摘得花生的全局最大数量
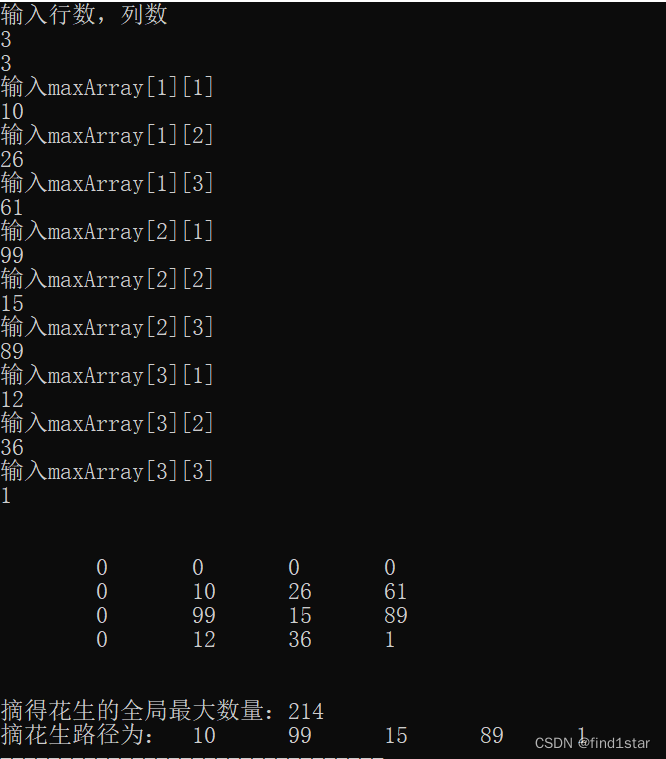
cout<<"摘得花生的全局最大数量:"<<maxarray[row][column]<<"\n";
//二、最大花生数量路径
int x = row,y=column,begin = 1,end = row+column-1;
cout<<"摘花生路径为:";
// 调用递归倒叙输出
recursion(begin,end,x,y,maxarray);
}
// 递归输出
void recursion(int begin , int end ,int x,int y,int maxarray[100][100]) {
if(begin<=end) {
if(maxarray[x][y-1] > maxarray[x-1][y]) {
recursion(begin+1,end,x,y-1,maxarray);
cout<<"\t"<<maxarray[x][y]-maxarray[x][y-1];
} else {
recursion(begin+1,end,x-1,y,maxarray);
cout<<"\t"<<maxarray[x][y]-maxarray[x-1][y];
}
} else {
return;
}
}



发表评论