一、设计动态规划算法的步骤
(1).找出最优解的性质
(2).动态规划方程
(3).自底向上计算最优值
二、矩阵连乘积问题
计算三个矩阵abc的成绩,由于矩阵乘法的性质,不同计算顺序导致的乘法运算量可能相差悬殊。即(ab)c 和a(bc)的运算量差距很大。
a:行数*列数 50*10 b:10*40 c:40*30
乘法运算次数:
(ab)c=(50*10*40)+50*40*30 =80000
a(bc)=50*10*30+(10*40*30)=27000
第二种计算方法的运算量是明显小于第一种的
三、分析最优解的结构
使用a[i,j]代表ai,ai+1...aj的连乘积,做一个断点k,i<=k<j,k将矩阵的连乘积分割为两部分,ai,ai+1...ak,ak+1...aj。以此,对乘积ai,ai+1...aj的完全加括号的代价就是计算ai,ai+1...ak,ak+1...aj的代价之和,再加上两者相乘的代价。
即:(ai,ai+1...ak)+(ak+1...aj)+pi-1pkpj
ai的维数为 ai-1*temp ai-1的原因是p[i]从0开始存储
//p[i]为行数,temp为列数
for(i=0;i<=n-1;i++)
scanf("%d%d",&p[i],&temp);
若ai,ai+1...aj的一个最优完全加括号方式是以k为断点,分割矩阵,则ai,ai+1...ak的子链必须是它的一个最优完全加括号方式。反之,若存在ai,ai+1...ak的一个代价更小的最优完全加括号方式,则它替换到ai,ai+1...aj中则会产生另一个最优解。这样一来,任何最优解都包含子问题的最优解。
四、建立递归关系
a[i,j]代表ai,ai+1...aj的连乘积,m[i][j]代表a[i][j]的最少次数。
a[1,n]代表a1,a2...an的连乘积,m[1][n]代表a[1,n]的最优解。
i,起始位置,j,终止位置。
当i=j,代表矩阵链只包含一个矩阵,a[1,1]代表矩阵链中只包含矩阵a1。
则m[i][i]=0.
i<j,在ai,ai+1...aj中加一个断点k,i<=k<j,则m[i][j]等于子乘积a[i,k]和a[k+1,j]的和在加上两个矩阵相乘的乘法运算次数(代价),乘法运算次数就是m*n 矩阵a * n*p 矩阵b = m *p 矩阵c
 图片来源:
图片来源:
https://www.cnblogs.com/beatrice7/p/4149639.html
定义数组s[i][j]保存k的值。
#include<bits/stdc++.h>
using namespace std;
#define num 51
int p[num];//行列数p[i-1]行数,p[i]为列数
int m[num][num];//保存最优解
int s[num][num];//保存断点k的值
int lookupchain(int i,int j)
{
if(m[i][j]>0)return m[i][j];//m[i][j]存了子问题的运算结果
if(i==j)return 0;//只含一个矩阵的情况。
int u = lookupchain(i,i)+lookupchain(i+1,j)+p[i-1]*p[i]*p[j];//递推公式,以i为第一个断点
s[i][j] = i;
for(int k=i+1;k<j;k++)//从i后找不同断点的情况,保存最小值为最优解m[i][j]
{
int t = lookupchain(i,k)+lookupchain(k+1,j)+p[i-1]*p[k]*p[j];
if(t<u){u=t;s[i][j]=k;}
}
m[i][j]=u;
return u;
}| 矩阵 | a1 | a2 | a3 | a4 | a5 | a6 |
| 行列数 | 50*10 | 10*40 | 40*30 | 30*5 | 5*20 | 20*15 |
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 值 | 50 | 10 | 40 | 30 | 5 | 20 | 15 |
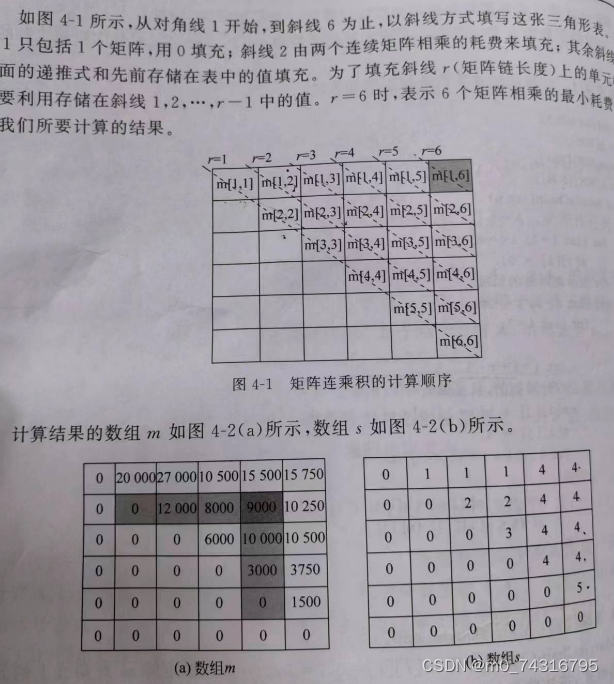
五、构建最优解
(a[i,k])(a[k+1,j]),令s[i][j]=k
则a[1,n]的最优加括号方式为(a([1,s[1][n]))(a(s[1][n]+1,n))
void traceback(int i,int j)
{
if(i==j)printf("a%d",i);
else
{
printf("(");
traceback(i,s[i][j]);
traceback(s[i][j]+1,j);
printf(")");
}
}完整代码为:
#include<bits/stdc++.h>
using namespace std;
#define num 51
int p[num];
int m[num][num];
int s[num][num];
int lookupchain(int i,int j)
{
if(m[i][j]>0)return m[i][j];
if(i==j)return 0;
int u = lookupchain(i,i)+lookupchain(i+1,j)+p[i-1]*p[i]*p[j];
s[i][j] = i;
for(int k=i+1;k<j;k++)
{
int t = lookupchain(i,k)+lookupchain(k+1,j)+p[i-1]*p[k]*p[j];
if(t<u){u=t;s[i][j]=k;}
}
m[i][j]=u;
return u;
}
void traceback(int i,int j)
{
if(i==j)printf("a%d",i);
else
{
printf("(");
traceback(i,s[i][j]);
traceback(s[i][j]+1,j);
printf(")");
}
}
int main()
{
int n;
scanf("%d",&n);
int i,temp;
for(i=0;i<=n-1;i++)
scanf("%d%d",&p[i],&temp);
p[n]=temp;
memset(m,0,sizeof(m));
lookupchain(1,n);
printf("%d\n",m[1][n]);
traceback(1,n);
return 0;
}
/*
input:
6
50 10
10 40
40 30
30 5
5 20
20 15
output:
15750
((a1(a2(a3a4)))(a5a6))
*/本博客资料、代码来源于清华大学出版社算法设计与分析,本博客仅用于个人学习,可能存在纰漏,敬请批评指正。




发表评论