一、图的基本概念
图是由顶点集合及顶点间的关系组成的一种数据结构:g = (v, e),其中:
- 顶点集合v = {x|x属于某个数据对象集}是有穷非空集合;
- e = {(x,y)|x,y属于v}或者e = {<x, y>|x,y属于v && path(x, y)}是顶点间关系的有穷集合,也叫做边的集合。
- (x, y)表示x到y的一条双向通路,即(x, y)是无方向的;path(x, y)表示从x到y的一条单向通路,即path(x, y)是有方向的。
顶点和边:图中结点称为顶点,第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边,图中的第k条边记作ek,ek = (vi,vj)或<vi,vj>。
有向图和无向图:在有向图中,顶点对<x, y>是有序的,顶点对<x,y>称为顶点x到顶点y的一条边(弧),<x, y>和<y, x>是两条不同的边,比如下图g3和g4为有向图。在无向图中,顶点对(x, y)是无序的,顶点对(x,y)称为顶点x和顶点y相关联的一条边,这条边没有特定方向,(x, y)和(y,x)是同一条边,比如下图g1和g2为无向图。注意:无向边(x, y)等于有向边<x, y>和<y, x>。
树和图:
- 树是一种特殊的图(无向,无环,连通)
- 图不一定是树
- 树关注的是节点中存储的值
- 图关注的是顶点及边的权值
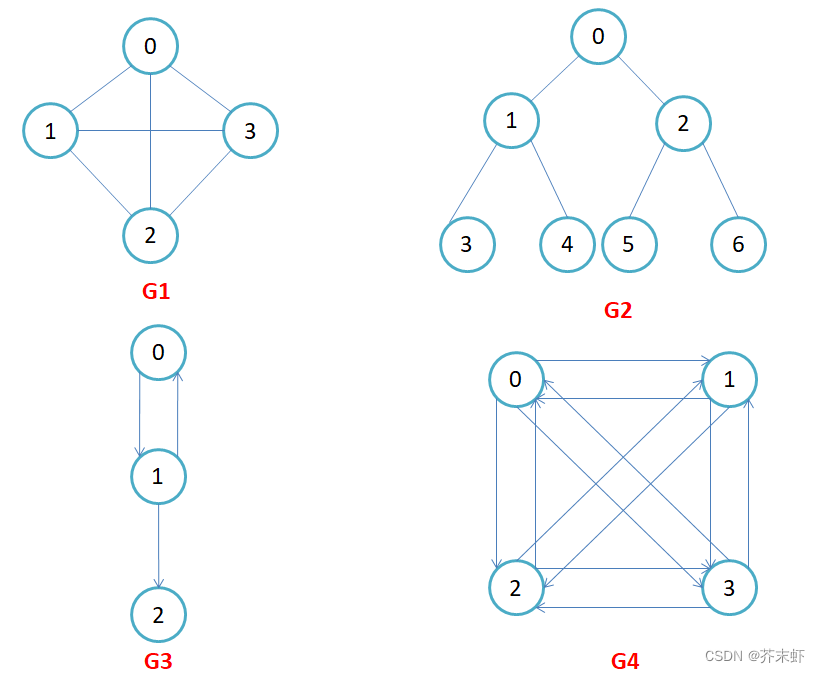
完全图:就是任意两个顶点之间都直接相连,是最稠密的图。在有n个顶点的无向图中,若有n * (n-1)/2(等差数列)条边,即任意两个顶点之间有且仅有一条边,则称此图为无向完全图,比如上图g1;在n个顶点的有向图中,若有n * (n-1)条边,即任意两个顶点之间有且仅有方向相反的边,则称此图为有向完全图,比如上图g4。
邻接顶点:在无向图中g中,若(u, v)是e(g)中的一条边,则称u和v互为邻接顶点,并称边(u,v)依附于顶点u和v;在有向图g中,若<u, v>是e(g)中的一条边,则称顶点u邻接到v,顶点v邻接自顶点u,并称边<u, v>与顶点u和顶点v相关联。
顶点的度:顶点v的度是指与它相关联的边的条数,记作deg(v)。在有向图中,顶点的度等于该顶点的入度与出度之和,其中顶点v的入度是以v为终点的有向边的条数,记作indev(v);顶点v的出度是以v为起始点的有向边的条数,记作outdev(v)。因此:dev(v) = indev(v) + outdev(v)。对于无向图,顶点的度等于该顶点的入度和出度,即dev(v) = indev(v) = outdev(v)。
路径:在图g = (v, e)中,若从顶点vi出发有一组边使其可到达顶点vj,则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。
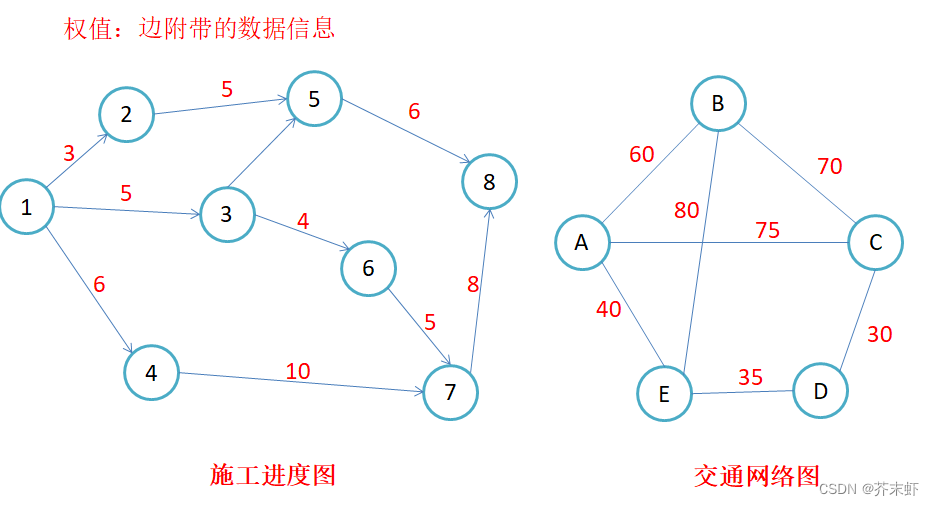
路径长度:对于不带权的图,一条路径的路径长度是指该路径上的边的条数;对于带权的图,一条路径的路径长度是指该路径上各个边权值的总和。
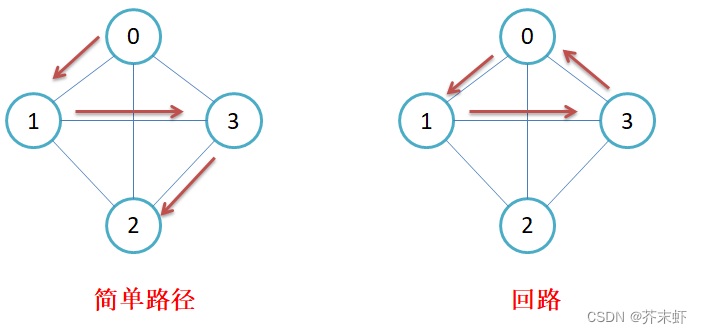
简单路径:若路径上各顶点v1,v2,v3,…,vm均不重复,则称这样的路径为简单路径。
回路:若路径上第一个顶点v1和最后一个顶点vm重合,则称这样的路径为回路或环。
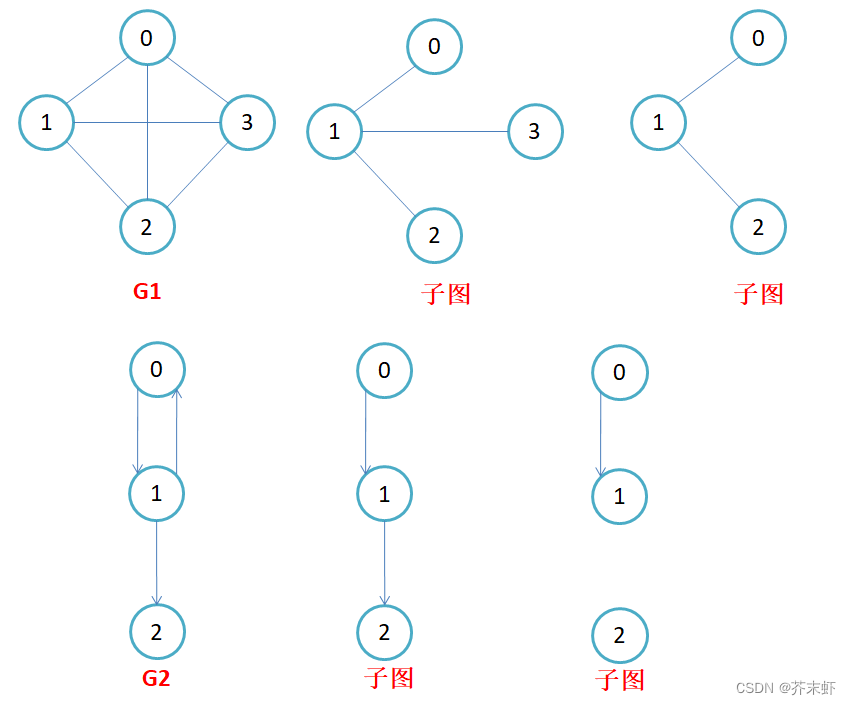
子图:设图g = {v, e}和图g1 = {v1,e1},若v1属于v且e1属于e,则称g1是g的子图。 顶点和边都是原图的一部分
连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。
强连通图:在有向图中,若在每一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在一条从vj到vi的路径,则称此图是强连通图。
生成树:在无向图中,一个连通图的最小连通子图称作该图的生成树。这里的最小指的是用最少的边连通所有的顶点,有n个顶点的连通图的生成树有n个顶点和n-1条边。 如下图中,无向图g1的生成树就可以是子图1。
二、图的存储结构
因为图中既有节点,又有边(节点与节点之间的关系),因此,在图的存储中,只需要保存:节点和边关系即可。节点保存比较简单,只需要一段连续空间即可,那边关系该怎么保存呢?
2.1 邻接矩阵
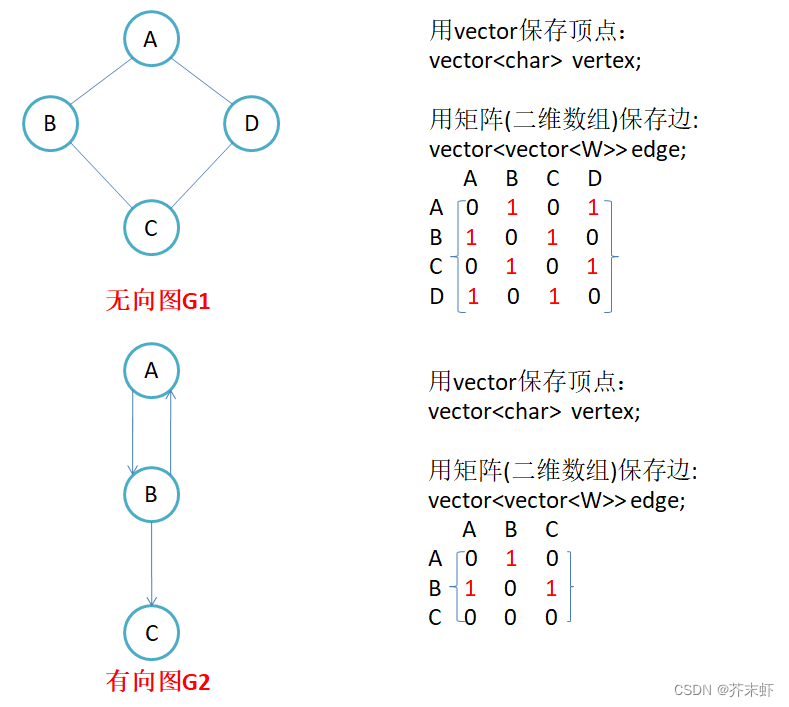
邻接矩阵:使用数组表示顶点的集合,使用矩阵(二维数组)表示边的关系。
因为节点与节点之间的关系就是连通与否,即为0或者1,因此邻接矩阵(二维数组)即是:先用一个数组将顶点保存,然后采用矩阵来表示节点与节点之间的关系。
注意:
- 无向图的邻接矩阵是对称的,第i行(列)元素个数之和,就是顶点i的度。有向图的邻接矩阵则不一定是对称的,第i行(列)元素个数之和就是顶点i 的出(入)度。
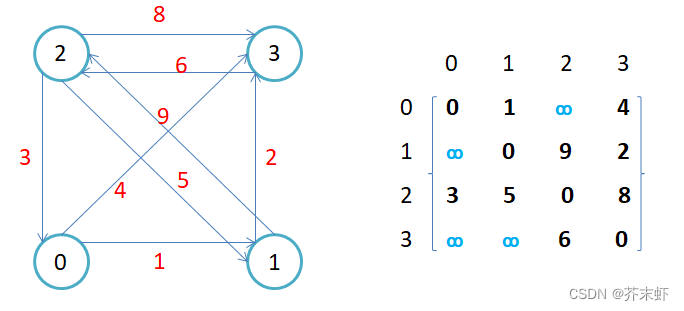
- 如果边带有权值,并且两个节点之间是连通的,上图中的边的关系就用权值代替,如果两个顶点不通,则使用无穷大代替。
邻接矩阵的实现
#include <vector>
#include <map>
#include <iostream>
using namespace std;
namespace matrix
{
template <class v, class w, w w_max = int32_max, bool direction = false>
class graph{
vector<v> _vertexs; //顶点集合
map<v, size_t> _indexmap; //顶点映射下标
vector<vector<w>> _matrix; //邻接矩阵
public:
graph() = default;
graph(const v* vertexs, size_t n)
{
_vertexs.reserve(n);
for(size_t i = 0; i < n; ++i)
{
_vertexs.push_back(vertexs[i]);
_indexmap.insert(make_pair(vertexs[i], i));
}
_matrix.resize(n);
for(vector<w>& e : _matrix)
{
e.resize(n, w_max);
}
}
size_t getindex(const v& vertex)
{
auto it = _indexmap.find(vertex);
if(it != _indexmap.end())
{
return it->second;
}
else
{
throw invalid_argument("不存在的顶点");
return uint32_max;
}
}
bool addedge(const v& src, const v& des, const w& w)
{
size_t s = getindex(src);
size_t d = getindex(des);
_matrix[s][d] = w;
if(!direction)
_matrix[d][s] = w;
}
void print()
{
//打印顶点和下标的映射关系
for(size_t i = 0; i < _vertexs.size(); ++i)
{
cout << "[" << i << "]";
cout << " --> ";
cout << _vertexs[i] << endl;
}
cout << endl;
//打印矩阵
cout << " ";
for(size_t k = 0; k < _matrix.size(); ++k)
cout << k << " "; // 打印列号
cout << endl;
for(size_t i = 0; i < _matrix.size(); ++i)
{
cout << i << " "; // 打印行号
for(size_t j = 0; j < _matrix[i].size(); ++j)
{
if(_matrix[i][j] == w_max)
cout << "∞ ";
else
cout << _matrix[i][j] << " ";
}
cout << endl;
}
}
};
};
邻接矩阵的优缺点
邻接矩阵的优点:
- 适合存储稠密图。
- 能够快速的判断两个顶点间的连接关系,并取到权值。o(1)
邻接矩阵的缺点:
- 不适合存储稀疏图,因为矩阵中存储了大量的0,比较浪费空间。
- 不方便查找一个顶点连接的所有边,需要遍历其他所有顶点。o(n)
2.2 邻接表
邻接表:使用数组表示顶点的集合,使用链表表示边的关系。
1.无向图邻接表存储
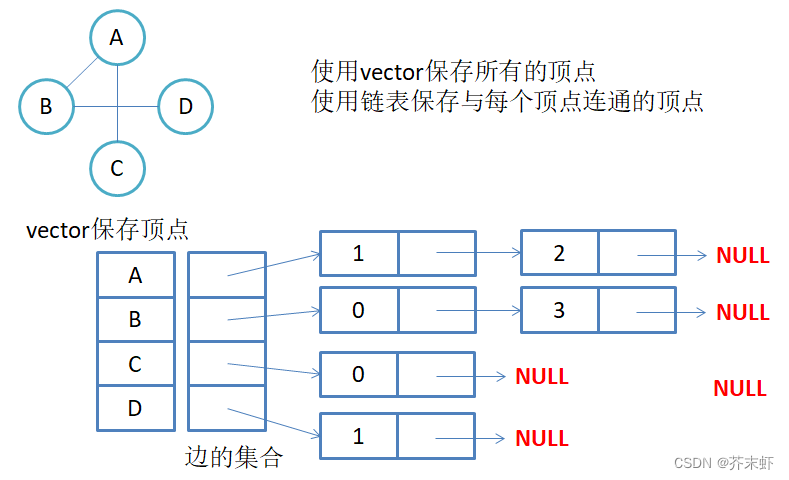
注意:无向图中同一条边在邻接表中出现了两次。如果想知道顶点vi的度,只需要知道顶点vi对应的边链表集合中结点的数目即可。
2.有向图邻接表存储
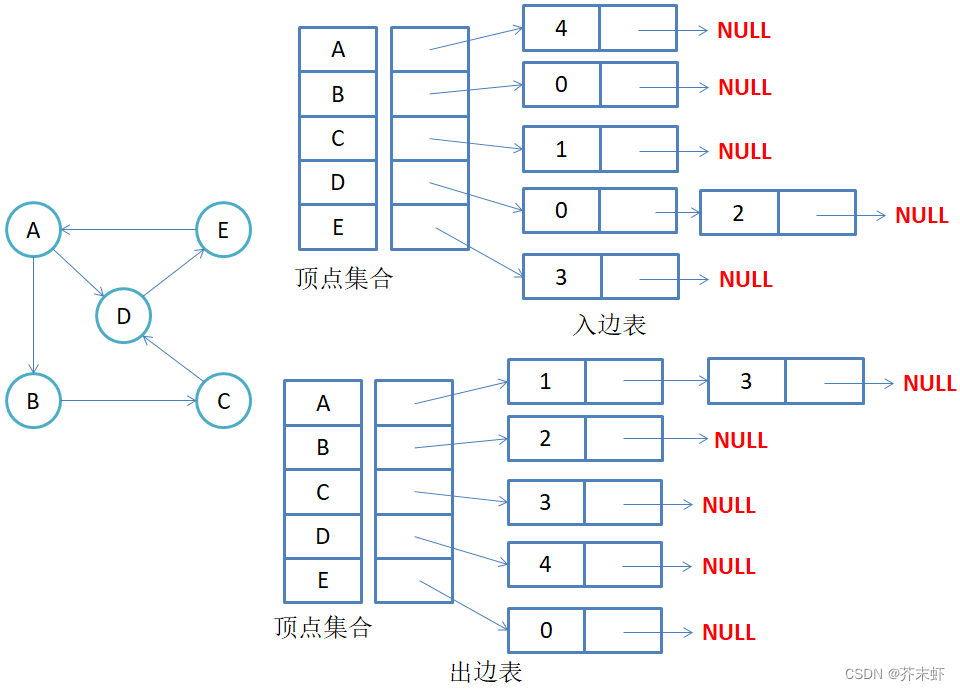
注意:有向图的邻接表存储分入边表和出边表。有向图中的每条边在邻接表中只出现一次。在出边表中,与顶点vi对应的边链表所含结点的个数,就是该顶点的出度;要得到vi顶点的入度,必须检测其他所有顶点对应的边链表,看有多少顶点的dst是vi,很不方便。 可以再建立一个入边表,在入边表中与顶点vi对应的边链表所含结点的个数,就是该顶点的入度,同理入边表不方便统计出度;
邻接表的实现
namespace link_table
{
template <class w>
struct edgenode
{
size_t _dsti; // 边的终点
w _w; // 边的权值
edgenode *_next; // 节点后继指针
edgenode(size_t dsti, w w)
: _dsti(dsti),
_w(w),
_next(nullptr)
{
}
};
template <class v, class w, bool direction = false>
class graph
{
typedef edgenode<w> edge;
vector<v> _vertexs; // 顶点集合
map<v, size_t> _indexmap; // 顶点映射下标
vector<edge *> _table; // 邻接表
public:
graph() = default;
graph(const v *vertexs, size_t n)
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; ++i)
{
_vertexs.push_back(vertexs[i]);
_indexmap.insert(make_pair(vertexs[i], i));
}
_table.resize(n, nullptr);
}
size_t getindex(const v &vertex)
{
auto it = _indexmap.find(vertex);
if (it != _indexmap.end())
{
return it->second;
}
else
{
throw invalid_argument("不存在的顶点");
return uint32_max;
}
}
bool addedge(const v &src, const v &des, const w &w)
{
size_t s = getindex(src);
size_t d = getindex(des);
edge *eg = new edge(d, w);
eg->_next = _table[s];
_table[s] = eg;
if (!direction)
{
edge *eg = new edge(s, w);
eg->_next = _table[d];
_table[d] = eg;
}
}
void print()
{
// 打印顶点和下标的映射关系
for (size_t i = 0; i < _vertexs.size(); ++i)
{
cout << "[" << i << "]";
cout << " --> ";
cout << _vertexs[i] << endl;
}
cout << endl;
// 打印邻接表
for (size_t i = 0; i < _table.size(); ++i)
{
cout << "[" << i << "]" << _vertexs[i] << "->";
edge *cur = _table[i];
while (cur != nullptr)
{
cout << "[" << cur->_dsti << "]" << _vertexs[cur->_dsti];
cout << ":" << cur->_w << "->";
cur = cur->_next;
}
cout << "nullptr" << endl;
}
}
};
};
邻接表的优缺点
邻接表的优点:
- 适合存储稀疏图。
- 适合查找一个顶点连接的所有边。(对于有向图,指的就是所有出边)
邻接表的缺点:
- 不方便确定两个顶点是否相连及权值
三、图的遍历
给定一个图g和其中任意一个顶点v0,从v0出发,沿着图中各边访问图中的所有顶点,且每个顶点仅被遍历一次。"遍历"即对结点进行某种操作的意思。
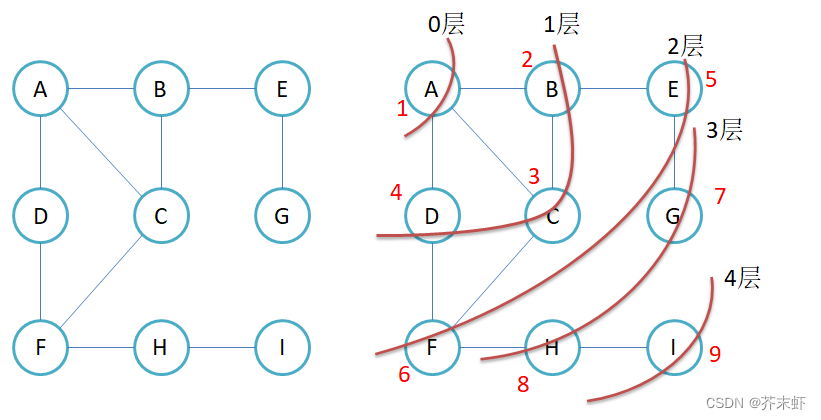
3.1 广度优先遍历
图的广度优先遍历(breadth-first search,bfs)是一种图的搜索算法,用于遍历图中的节点,从起始节点开始逐层遍历,先访问离起始节点最近的节点,再访问稍远一层的节点,以此类推。bfs通常使用队列来辅助遍历。
bfs的基本思路如下:
- 将起始节点加入队列,并将其标记为已访问
- 从队列中取出一个节点,访问并将该节点的相邻节点加入队列,标记相邻节点为已访问。
- 重复步骤2,直到队列为空
bfs的复杂度
- 时间复杂度:对于dfs,bfs遍历来说,时间复杂度和存储结构有关:
- 若采用邻接矩阵存储,时间复杂度为o(n^2); 注意不是n*e
- 若采用邻接链表存储,时间复杂度为o(n+e);
- 空间复杂度为 o(v),因为需要使用队列来保存节点。(最坏情况:围成一个圈)
代码实现:
void bfs(const v &start)
{
queue<int> que; // 队列
vector<bool> visited(_vertexs.size(), false); // 标记数组
// 将起点入队,标记
int starti = getindex(start);
que.push(starti);
visited[starti] = true;
int d = 1; // 当前层的节点数,用于控制逐层遍历
while (!que.empty())
{
while (d--)
{
int front = que.front();
que.pop();
cout << "[" << front << "]" << _vertexs[front] << " ";
for (int i = 0; i < _vertexs.size(); ++i)
{
if (_matrix[front][i] != w_max && !visited[i])
{
que.push(i);
visited[i] = true;
}
}
}
d = que.size();
cout << endl;
}
}
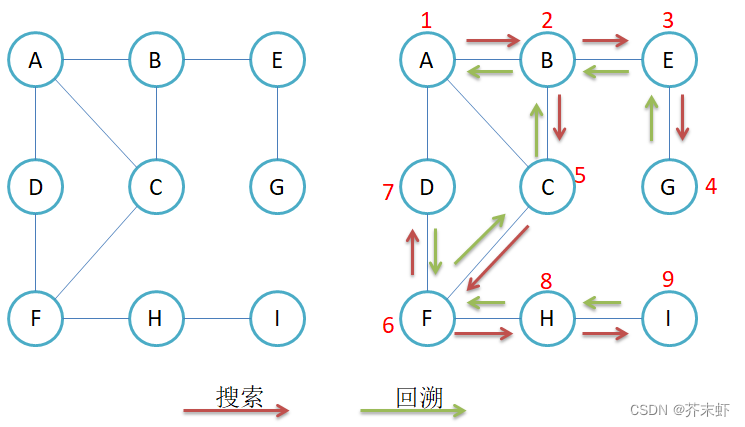
3.2 深度优先遍历
深度优先遍历(depth first search, dfs)是一种用于遍历图或树的算法,它的主要特点是尽可能深地搜索树的分支,当节点的一个分支被完全搜索过后,它会回溯到发现该节点的上一个节点,继续搜索其他路径。这个过程一直持续到所有从源节点可达的节点都被访问为止。
在深度优先遍历中,通常使用递归或栈来实现。递归版本通常更简洁,因为它利用了函数调用的栈来模拟显式的栈操作。非递归版本则更适用于需要明确控制栈的情况,比如当递归可能导致栈溢出时。
深度优先遍历的具体步骤可以概括为:
- 访问初始节点,并标记为已访问。
- 查找初始节点的第一个未被访问的邻接点。
- 如果邻接点存在且未被访问,递归地进行深度优先遍历。
- 回溯到初始节点,并尝试访问其下一个未被访问的邻接点。
- 如果所有邻接点都被访问过,回溯到上一个访问过的节点,继续访问其未被访问的邻接点。
- 重复上述步骤,直到所有节点都被访问过。
dfs的复杂度
- 时间复杂度:对于dfs,bfs遍历来说,时间复杂度和存储结构有关:
- 若采用邻接矩阵存储,时间复杂度为o(n^2); 注意不是n*e
- 若采用邻接链表存储,时间复杂度为o(n+e);
- 空间复杂度为 o(v),因为递归调用会使用系统栈来保存调用信息。(最坏情况:连成一条线)
代码实现:
void dfs(const v &start)
{
int starti = getindex(start);
vector<bool> visited(_vertexs.size(), false);
_dfs(starti, visited);
}
void _dfs(int index, vector<bool> &visited)
{
cout << "[" << index << "]" << _vertexs[index] << endl;
visited[index] = true;
for (int i = 0; i < _vertexs.size(); ++i)
{
if (_matrix[index][i] != w_max && !visited[i])
{
_dfs(i, visited);
}
}
}
下一篇:【高阶数据结构】图 {最小生成树:kruskal算法,prim算法;最短路径:dijkstra算法,bellman-ford算法,floyd算法}




发表评论