上一篇文章,我们已经模拟实现了一些栈的方法,本篇文章我们将介绍一些栈的应用场景,敬请期待吧~就觉得小编讲的还可以的可以留个关注支持一下~
1.将递归转化为循环
逆序打印列表
递归打印与其他方法不同,我们先看代码
void printlist(node head){
if(null != head){
printlist(head.next);
system.out.print(head.val + " ");
}
}我们借助图片来理解
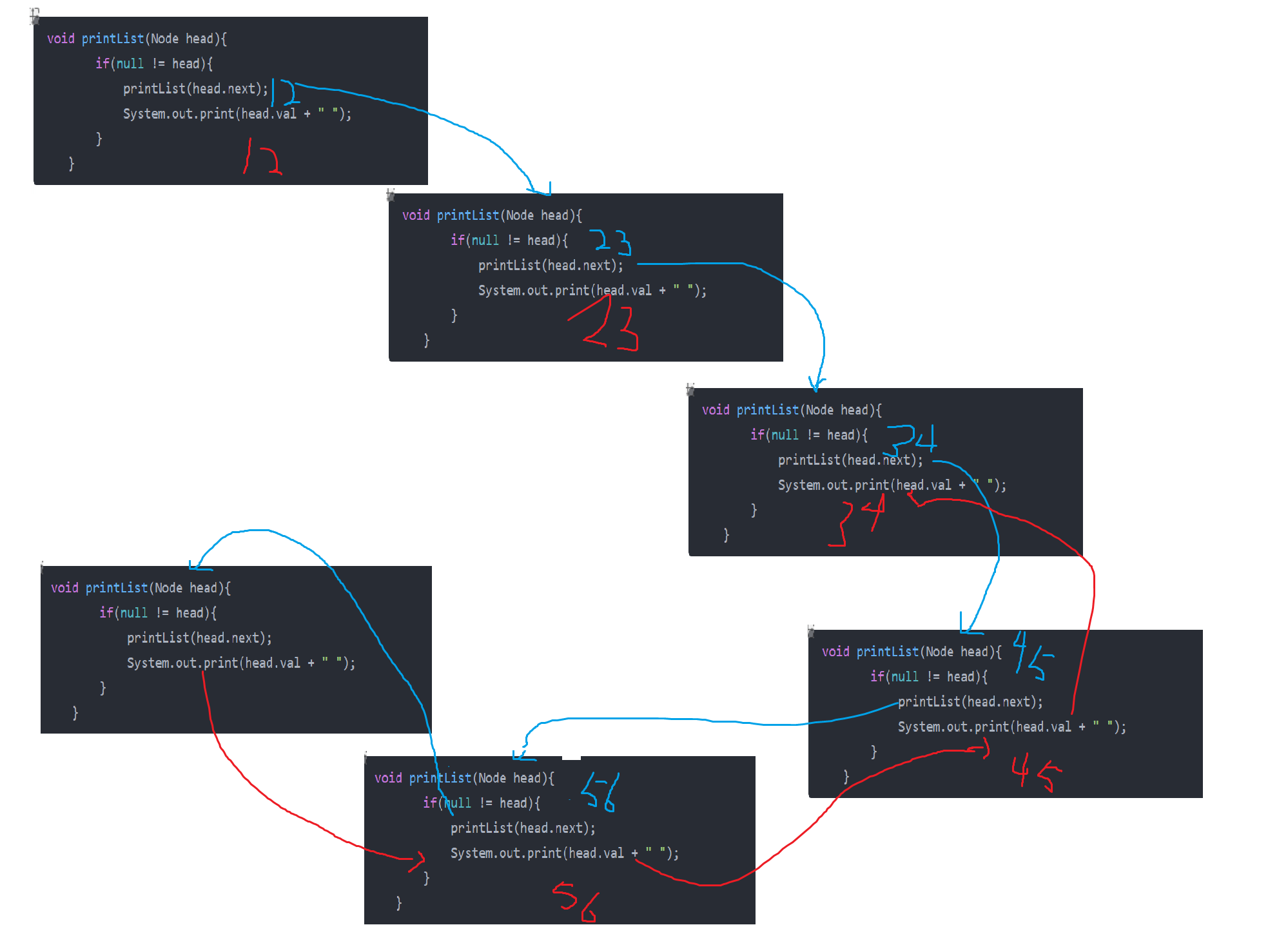
以上就是递归的全过程 ,每次调用方法,都会在栈上开辟栈帧,如图
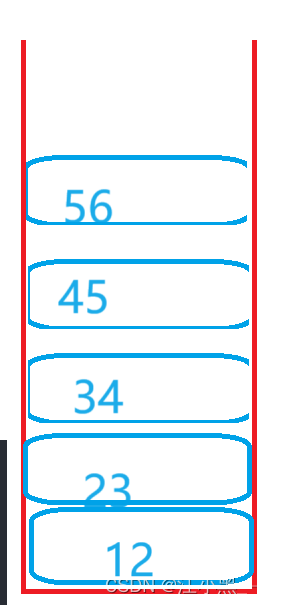
所以,我们可以申请一个栈,将所有节依次放入,在依次弹出,即为逆序打印
代码如下
public void reverseprintf(){
stack<listnode> stack = new stack<>();
listnode cur = head;
while (cur != null){
stack.push(cur);
cur = cur.next;
}
while (!stack.isempty()){
listnode top = stack.pop();
system.out.println(top.val);
}
}调用测试
public static void main(string[] args) {
mysinglelist mysinglelist = new mysinglelist();
mysinglelist.addlast(12);
mysinglelist.addlast(23);
mysinglelist.addlast(34);
mysinglelist.addlast(45);
mysinglelist.addlast(56);
mysinglelist.display();
mysinglelist.reverseprintlist();
}运行截图
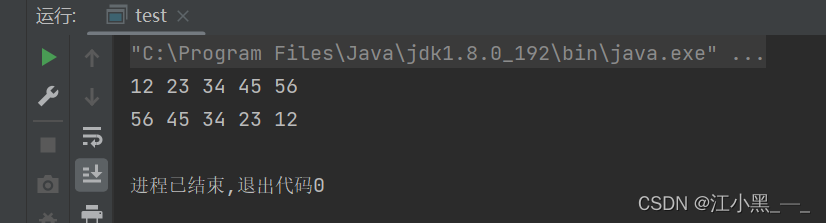
相对于递归,用栈的方法将其打印是不是更加方便呢~
2.括号匹配
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号
思路,将左括号放进栈中,如果遇到右括号直接匹配即可,如图我们先看不匹配的情况
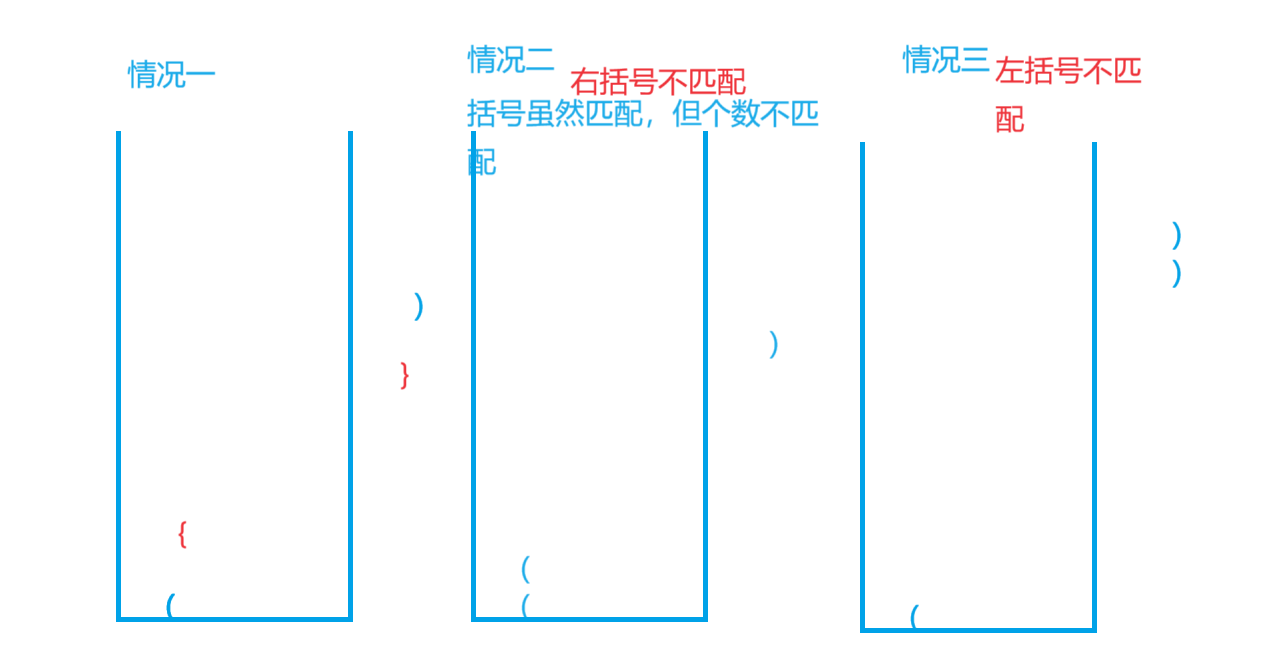
接下来看匹配的情况
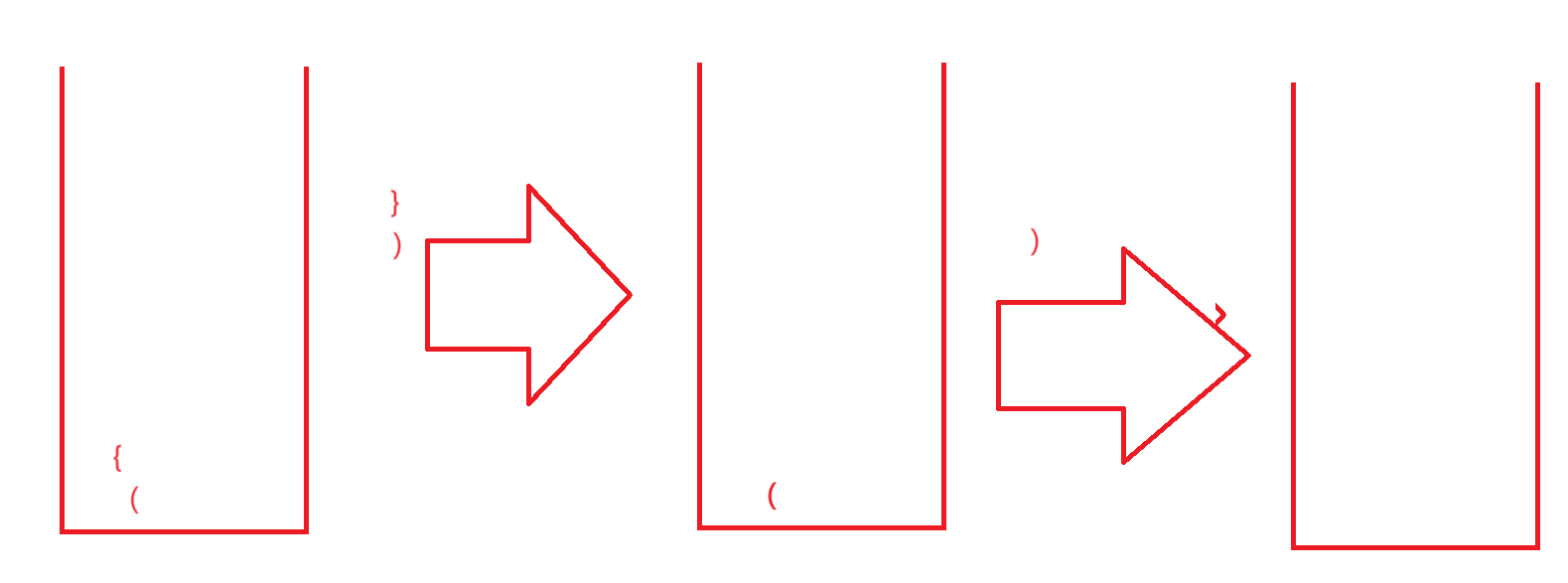
括号匹配,栈顶元素弹出,栈外第一个元素向后走1步,以此类推,直到字符串遍历完成,栈为空
此时还有一种特殊情况

代码如下
public boolean isvalid(string s){
stack<character> stack = new stack<>();
for (int i = 0;i<s.length();i++){
char ch = s.charat(i);
if (ch =='('||ch == '{'||ch == '[' ){
//左括号
stack.push(ch);
}else {
//右括号
if (stack.isempty()){
return false;
}
char top = stack.peek();
//此时top是左括号。ch是右括号
if (ch==')'&&top == '('||ch=='}'&&top == '{'||ch==']'&&top == '['){
stack.pop();
}else {
return false;
}
}
}
if (!stack.isempty()){
return false;
}
return true;
}3.逆波兰表达式
逆波兰表达式又叫做 后缀表达式 。 逆波兰表示法是波兰 逻辑学家 j・卢卡西维兹 (j・ lukasiewicz)于1929年首先提出的一种表达式的表示方法 。 后来,人们就把用这种表示法写出的表达式称作“逆波兰表达式”。 逆波兰表达式把运算量写在前面,把算符写在后面
举个例子:
中缀表达式:a+b*c+(d*e+f)*g
后缀表达式:abc*+de*f+g*+
将中缀表达转换为后缀表达式的具体步骤
1.从左到右先乘除后加减,,依次加括号
如图
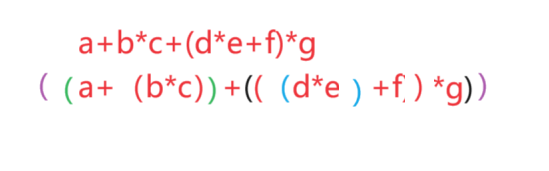
2.将运算符挪到对应括号的外面
((a(bc)*)+(((de)*f)+g)*)+
3.去掉所有括号
abc*+de*f+g*+
我申请一个栈,进行遍历
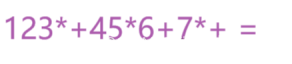

上面的例子大家仔细理解~- 我们继续往下看~
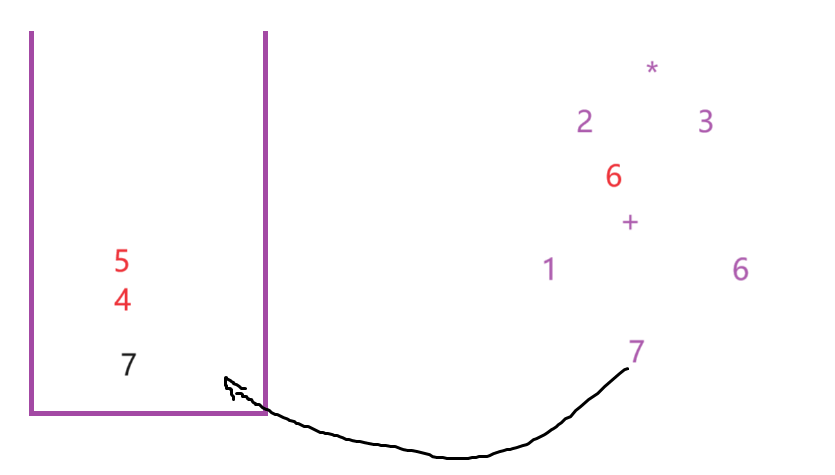
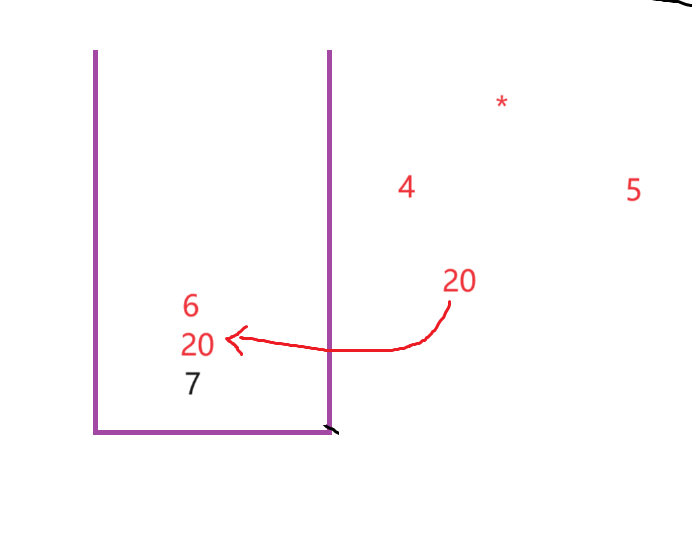
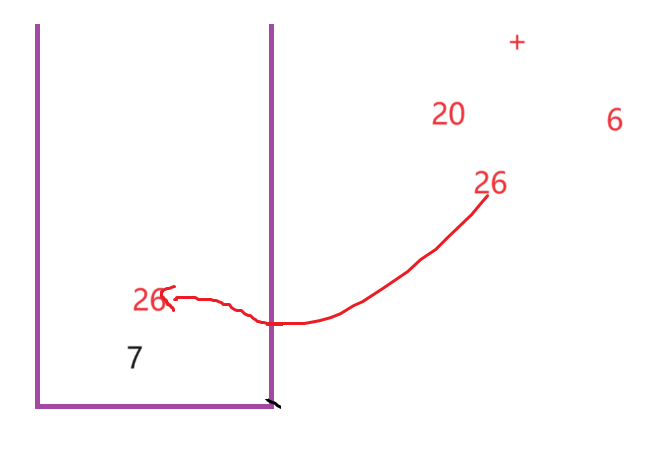
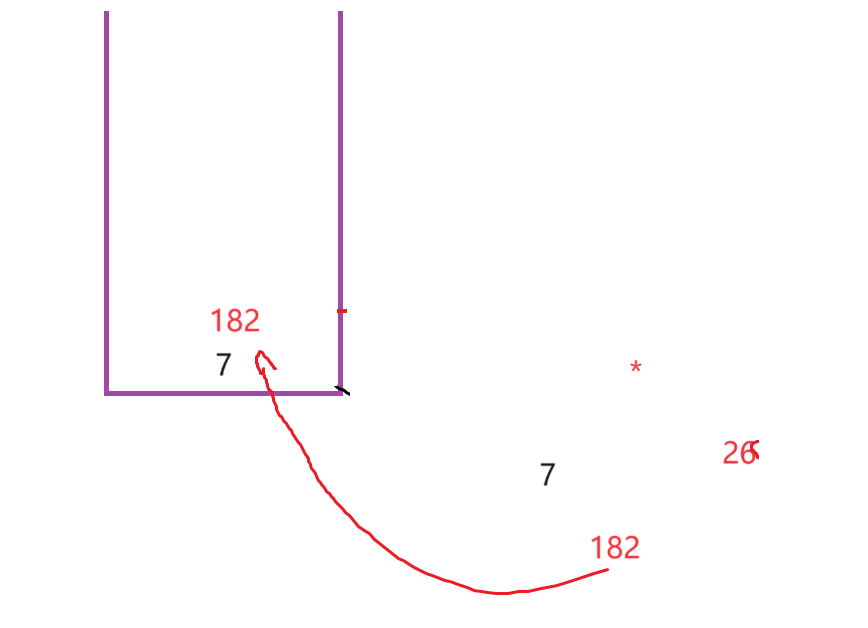
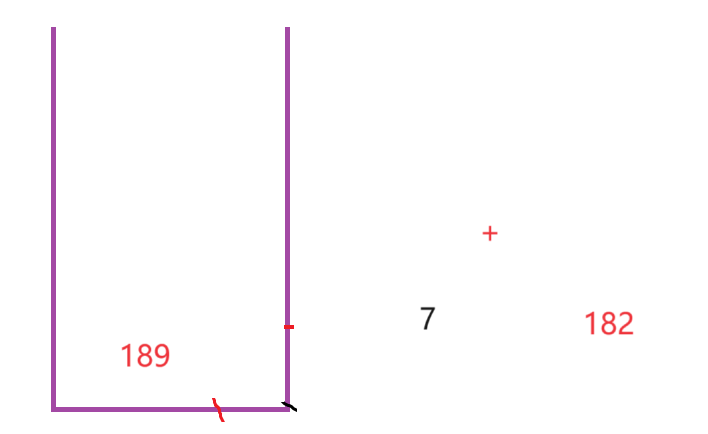
此时你会发现,后缀表达式和中缀表达式的结果完全一样,其实,这也就是简单计算机的底层逻辑!
public int evalrpe(string []tokens){
stack <integer> stack = new stack<>();
for (string s:tokens){
if (!isoperation(s)){
stack.push(integer.parseint(s));
}else {
int num2 = stack.pop();
int num1 = stack.pop();
switch (s){
case "+":
stack.push(num1+num2);
break;
case "-":
stack.push(num1-num2);
break;
case "*":
stack.push(num1*num2);
break;
case "/":
stack.push(num1/num2);
break;
}
}
}
return stack.pop();
}
public boolean isoperation(string s){
if (s.equals("+")||s.equals("-")||s.equals("*")||s.equals("/")){
return true;
}
return false;
}
请大家结合图片与代码进行理解,那么到此为止,帮我那边文章就结束了,下一篇文章,我们将继续讲解一些例题,敬请期待 ~




发表评论