聚类算法
算法概括
聚类(clustering)
聚类的概念
聚类的要求
聚类与分类的区别
之前学习过k近邻算法分类算法,分类和聚类听上去好像很相似,但是两者完全是不同的应用和原理。
例如,根据下图的四个属性进行预测某一输入的所属类别:
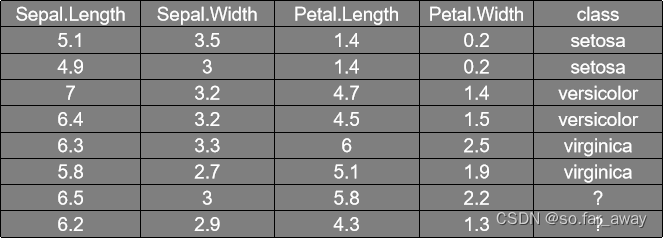
概括而来就是这样一个流程:
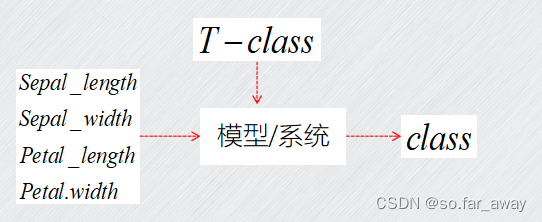
可以看出训练样本是有明确的标签的,数据点是有已知结果的,而聚类不同,聚类算法本身训练的样本就是无标签的,你不知道它属于哪一类,而把具有空间相近性、性质相似性的数据点归为一类,这就是聚类算法要做的事情。
还是上面的例子:
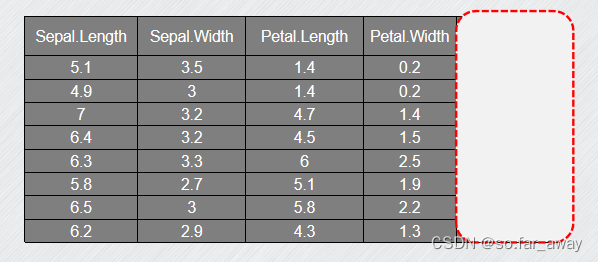
这个时候训练样本的标签被盖住了,我们必须从这四个属性入手,把样本聚合成不同的簇,每个簇中的数据点的属性最相似。
概括而来就是这样一个过程:

现在小结一下,分类和聚类的区别概括而来就是这样:
常见算法分类
聚类算法中存在的问题
距离度量
评估两个不同样本之间的“相似性”,通常使用的方法就是计算两个样本之间的“距离”,使用不同的方法计算样本间的距离关系到聚类结果的好坏。
大多数聚类分析是以相似性计算为基础的,同一个聚类中的个体模式相似,不在同一个聚类中的个体模式则相异。目前,相似性距离的计算都是基于向量的,也就是计算两个向量的距离,距离相近则相似度越大。
下面,介绍几种常见的距离计算方法。
闵可夫斯基距离
闵可夫斯基距离计算距离如下:
import numpy as np
x=np.random.random(10)
y=np.random.random(10)
dist=np.linalg.norm(x-y,ord=4)#闵可夫斯基距离,此时p=4
欧式距离(欧几里得距离)
欧式距离计算举例如下:
import numpy as np
import scipy.spatial.distance as dis
x=np.random.random(10)
y=np.random.random(10)
x=np.vstack([x,y])
dist=dis.pdist(x,metric='euclidean')
#或者直接按照闵可夫斯基距离的计算方式
dist=np.linalg.norm(x-y,ord=2)
曼哈顿距离
曼哈顿距离计算python语句如下:
import numpy as np
x=np.random.random(10)
y=np.random.random(10)
dist=np.linalg.norm(x-y,ord=1)
切比雪夫距离
切比雪夫距离计算python语句如下:
import numpy as np
x=np.random.random(10)
y=np.random.random(10)
dist=np.linalg.norm(x-y,ord=np.inf)
皮尔逊相关系数
皮尔逊相关系数计算python语句如下:
import numpy as np
import scipy.spatial.distance as dis
x=np.random.random(10)
y=np.random.random(10)
x=np.vstack([x,y])
dist=1-dis.pdist(x,metric='correlation')
余弦相似度
import numpy as np
import scipy.spatial.distance as dis
x=np.random.random(10)
y=np.random.random(10)
x=np.vstack([x,y])
dist=1-dis.pdist(x,metric='cosine')
杰卡德相似系数
杰卡德相似距离计算python语句如下:
import numpy as np
import scipy.spatial.distance as dis
x=np.random.random(10)
y=np.random.random(10)
x=np.vstack([x,y])
dist=dis.pdist(x,metric='jaccard')
划分聚类
k-means聚类算法
算法原理
基本概念
算法实例
题目背景
k-means的手动实现
import numpy as np
def kmeans(x, k, max_iter=300):
# 随机选择k个初始质心
centroids = x[np.random.choice(x.shape[0], k)]
for i in range(max_iter):
# 计算每个样本点到质心的距离,并分配到最近质心所在的簇中
distances = np.sqrt(((x - centroids[:, np.newaxis])**2).sum(axis=2))
labels = distances.argmin(axis=0)
# 重新计算每个簇的质心
new_centroids = np.array([x[labels == j].mean(axis=0) for j in range(k)])
# 检查质心是否变化,若没有则退出
if np.all(centroids == new_centroids):
break
centroids = new_centroids
return labels, centroids
x=np.array([[170,70],[178,75],[100,100],[120,40],[10,0.1]])
labels,centroids=kmeans(x,k=2)
print("当k=3时,簇划分情况为:",labels)
print("当k=3时,质心为:\n",centroids)
sklearn库中k-means算法
import numpy as np
from sklearn.cluster import kmeans
#使用k-means算法对数据进行聚类
x=np.array([[170,70],[178,75],[100,100],[120,40],[10,0.1]])
kmeans_model=kmeans(n_clusters=2,init="k-means++")
kmeans_model.fit(x)
print("当k=2时,簇划分情况为:",kmeans2_model.labels_)
print("当k=2时,质心为:\n",kmeans2_model.cluster_centers_)
聚类分析的度量
聚类评价指标
簇内平方和(inertia)
轮廓系数(silhouette coefficient)
簇类个数k的调整(了解)
选择正确的聚簇数
相似性度量
初始聚类中心的选择
k-means算法的初值敏感,容易陷入局部最小值,同一个算法运行两次有可能得到不同的结果,所以建议初始选点可以根据多次交叉去做,选择多次中心点。




发表评论