注意:本文引用自专业人工智能社区venus ai
更多ai知识请参考原站 ([www.aideeplearning.cn])
高斯混合模型(gmm)是统计模型中的一颗璀璨之星,它为数据提供了一种复杂而又强大的表示方法。在机器学习的许多领域,从模式识别到图像处理,gmm都被广泛地采用和研究。它背后的核心思想是使用多个高斯分布的组合来拟合数据,这种方法的优越性在于其对数据的弹性拟合能力和生成性质。
1. 算法解读
gmm 是一种使用高斯分布混合体来表示数据集的方法。简单来说,每一个聚类都可以用一个高斯分布来描述,而数据集则可以被认为是这些高斯分布的混合。gmm的目标是:找出最能代表数据的高斯分布的参数(均值、协方差和混合系数)。
em(期望最大化)算法通常用于优化gmm的参数。em算法迭代地执行以下两个步骤:
期望步骤 (e-step):给定当前的模型参数,计算数据点属于每个聚类的概率。
最大化步骤 (m-step):更新模型参数以最大化观测数据的似然。
具体的数学基础知识请详见数学专栏。
2. 步骤和细节
初始化阶段:
选择高斯混合模型(gmm)中的高斯分布数量。
初始化每个高斯分布的参数,包括均值、协方差和混合系数。
e-step (期望步骤):
对每个数据点,根据当前参数估计,计算其属于各个高斯分布的后验概率。
m-step (最大化步骤):
更新均值: 根据后验概率,重新计算每个高斯分布的均值。
更新协方差: 根据后验概率,重新计算每个高斯分布的协方差。
更新混合系数: 重新估计每个高斯分布的混合系数。
收敛性检查:
判断算法是否已经收敛,这通常基于数据的对数似然或者模型参数的变化。
迭代:
如果模型尚未收敛,则回到e-step,继续迭代过程。
3. 举例
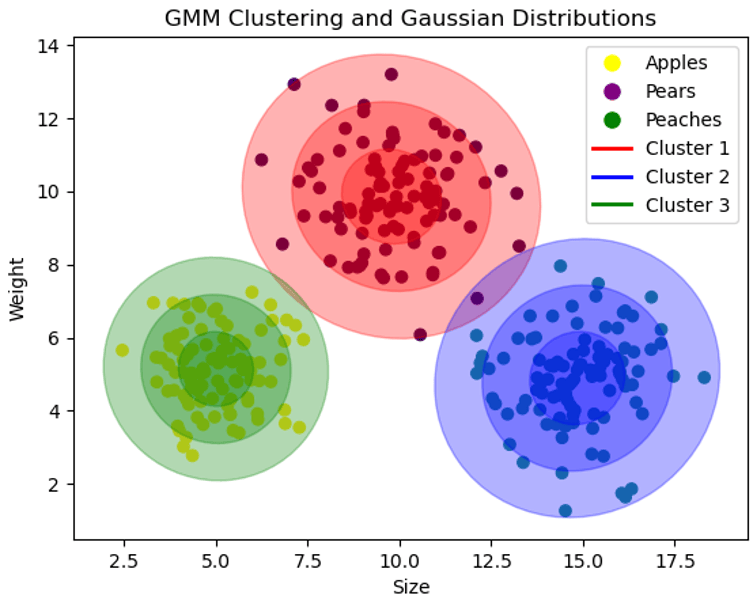
想象你在一个果园,这个果园里有苹果、梨和桃子三种水果。每种水果的大小和重量都有一定的特点。gmm就像是我们用来描述这些水果特点的工具。在这个模型中,我们用三个“高斯分布”(简单来说,就是一种特殊的图形或曲线)来分别描述苹果、梨和桃子的大小和重量。
每个高斯分布都可以被看作是一条“曲线”,这条曲线的形状由三个参数决定:均值(中心位置)、协方差(宽度或形状)和混合系数(高度)。gmm的目标就是调整这些曲线,让它们尽可能准确地描述每种水果的特点。
em(期望最大化)算法
em算法就像是我们调整这些曲线的方法。它分为两个步骤:e-step(期望步骤)和m-step(最大化步骤)。
e-step(期望步骤):
在这一步,我们看每个水果(数据点),根据当前的曲线,估计这个水果是苹果、梨还是桃子的概率。
m-step(最大化步骤):
接着,我们根据上一步得到的概率,调整我们的曲线,让它们更好地符合实际的水果分布。
我们不断重复这两个步骤,直到曲线基本不再改变,也就是找到了最适合描述水果特点的曲线。
步骤和细节:
初始化阶段: 我们首先要确定有几种水果(几个高斯分布)。然后,随便画几个曲线作为开始(初始化参数)。
e-step: 对每个水果,估计它属于苹果、梨和桃子的概率。在e-step中,我们计算了每个数据点属于每个高斯分布的概率,这个概率可以看作是该数据点对该高斯分布均值更新的权重。权重越高,说明这个数据点更有可能由这个高斯分布生成,因此应该对这个高斯分布的均值有更大的影响。这里的“权重”就像是我们对每个水果是来自苹果树、梨树还是桃树的“信心”或“猜测”。例如,我们看到一个红色的圆形水果,我们可能会猜测这有70%的可能是苹果,10%的可能是桃子,20%的可能是梨。
m-step: 根据刚刚估计的概率,调整我们的曲线。具体来说,我们会这样调整:
更新均值:根据每个数据点属于该高斯分布的概率权重,计算所有数据点的加权平均值,作为新的均值。
更新协方差:同样根据每个数据点属于该高斯分布的概率权重,计算数据点与新均值之间差异的加权平均值,作为新的协方差。
更新混合系数:计算所有数据点属于该高斯分布的概率的平均值,作为新的混合系数。
继续刚才的例子,如果我们看一个水果,觉得它有70%的可能性是苹果,20%的可能性是梨,10%的可能性是桃子。那么,当我们计算苹果的平均大小和重量时(属于苹果的高斯分布),当前这个水果就会以70%的“力量”(权重)参与其中;计算梨的高斯分布时,它会以20%的“力量”参与;计算桃子的高斯分布时,它会以10%的“力量”参与。
在m-step中,我们根据这些权重来更新高斯分布的参数。具体来说,每个数据点对高斯分布参数的贡献是按照它的权重来的,这就是为什么我们计算所有数据点的加权平均值作为新的参数。这样做的目的是最大化整个数据集的似然,也就是使得我们的模型更有可能生成观测到的数据。
这个加权平均值实际上是在求解一个优化问题:找到均值参数,使得模型对观测数据的似然最大。这个过程可以通过数学推导得到,但直观上理解,就是让每个数据点根据其属于该高斯分布的概率来共同决定这个高斯分布的均值。
收敛性检查: 查看曲线是否还在改变。如果基本不再改变,我们就找到了最好的曲线;如果还在变,就继续调整。
迭代:如果曲线还在变,我们就重复e-step和m-step,直到找到最适合的曲线。
代码实现:
为了模拟这个例子,我们可以生成一些来自不同高斯分布的数据点,这些分布代表了不同种类的水果的大小和重量。然后,我们将使用高斯混合模型(gmm)来拟合这些数据点,估计原始的高斯分布参数。
我们可以使用python的sklearn库中的gaussianmixture类来实现gmm。下面是相关代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import gaussianmixture
# 设置随机种子以保证结果的可重复性
np.random.seed(0)
# 创建三种水果的数据点(大小和重量)
# 每种水果由一个高斯分布代表
apples = np.random.multivariate_normal(mean=[5, 5], cov=[[1, 0], [0, 1]], size=100)
pears = np.random.multivariate_normal(mean=[10, 10], cov=[[2, 0], [0, 2]], size=100)
peaches = np.random.multivariate_normal(mean=[15, 5], cov=[[1.5, 0], [0, 1.5]], size=100)
# 将所有水果数据合并成一个数据集
fruits = np.vstack([apples, pears, peaches])
# 可视化原始数据点
plt.scatter(apples[:, 0], apples[:, 1], label='apples')
plt.scatter(pears[:, 0], pears[:, 1], label='pears')
plt.scatter(peaches[:, 0], peaches[:, 1], label='peaches')
plt.xlabel('size')
plt.ylabel('weight')
plt.title('original fruits data')
plt.legend()
plt.show()
# 使用gmm拟合数据
gmm = gaussianmixture(n_components=3, random_state=0)
gmm.fit(fruits)
# 提取gmm模型参数
means = gmm.means_
covariances = gmm.covariances_
# 输出gmm模型参数
print("means:", means)
print("covariances:", covariances)代码的结果如下:
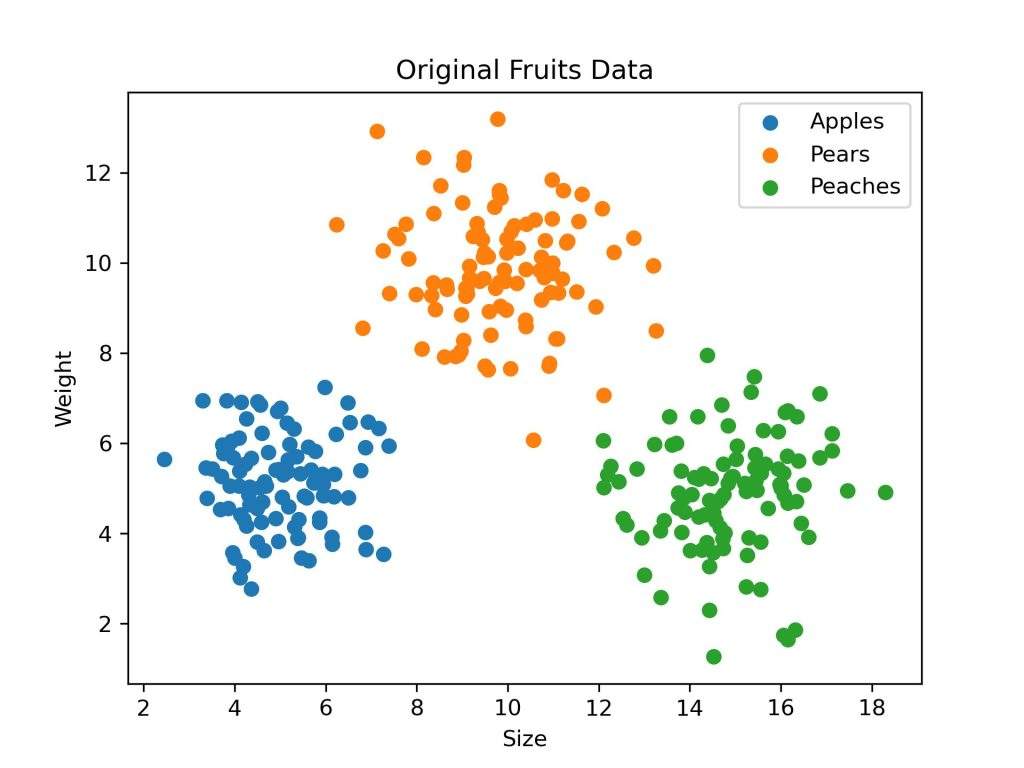
4. 算法评价
优点:
软聚类: gmm属于软聚类方法,它为每个数据点分配属于每个类的概率,而不是硬分配到某一类。这使得gmm能够表达不确定性,适用于模糊边界的情况。
聚类形状的灵活性: 由于使用了协方差矩阵,gmm可以形成各种形状的聚类,包括椭圆形、圆形和拉伸形状,而不仅仅是球形聚类。
参数估计: gmm不仅可以进行聚类,还可以估计数据的生成模型参数(均值、协方差和混合系数),这在某些应用中是有价值的。
缺点:
计算复杂性: gmm的训练过程涉及到期望最大化(em)算法,这通常需要更多的计算资源和时间,特别是当数据集很大时。
初始化敏感性: gmm的结果可能受到初始化的影响,不同的初始化可能导致不同的聚类结果。
选择组件数量: 在应用gmm之前,需要预先确定混合组件的数量(高斯分布的数量),这通常需要领域知识或通过交叉验证等方法来确定。
可能的奇异性问题: gmm可能遇到协方差矩阵接近奇异矩阵的问题,这会导致算法的不稳定。
对异常值敏感: 由于gmm基于概率密度,它对异常值或噪声点可能较为敏感。
5. 算法的变体
带有协方差约束的gmm:为了避免过度拟合或简化模型,可以对gmm中的协方差矩阵施加约束。常见的约束包括:
球形协方差:所有的聚类都有相同的方差,并且协方差矩阵是对角的。
对角协方差:协方差矩阵是对角的,但各个聚类的方差可能不同。
完全协方差:没有对协方差矩阵施加任何约束,允许聚类呈现任意椭圆形状。
gmm是一种极其强大的聚类方法,尤其适用于数据中存在多个潜在子群体的情况。通过为每个数据点提供属于每个聚类的概率信息,它提供了对数据的更丰富的解释。由于其参数化和生成性质,它还被广泛用于异常检测、图像分割和声学模型等领域。 尽管gmm在多个领域中都有卓越的应用,但其计算复杂性和需要预先指定高斯分布数量的要求有时可能会限制其实用性。为此,研究者已经提出了多种变体和优化方法。




发表评论