目录
floodfill算法简介:floodfill(泛洪填充)算法是一种图像处理的基本算法,用于填充连通区域。该算法通常从一个种子点开始,沿着种子点的相邻像素进行填充,直到遇到边界或者其他指定的条件为止。floodfill 算法的主要应用是在图像编辑软件中实现填充操作,以及在计算机图形学、计算机视觉等领域中进行区域填充。
下面我们通过一些题目来理解这个算法思想:
一.图像渲染:
- 题目链接:733. 图像渲染 - 力扣(leetcode)
- 题目描述:
有一幅以 m x n 的二维整数数组表示的图画 image ,其中 image[i][j] 表示该图画的像素值大小。
你也被给予三个整数 sr , sc 和 newcolor 。你应该从像素 image[sr][sc] 开始对图像进行 上色填充 。
为了完成 上色工作 ,从初始像素开始,记录初始坐标的 上下左右四个方向上 像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应 四个方向上 像素值与初始坐标相同的相连像素点,……,重复该过程。将所有有记录的像素点的颜色值改为 newcolor 。
最后返回 经过上色渲染后的图像 。 
- 对应函数签名如下:

代码详解:
解法一:
class solution {
//记录走过的路径,防止走回头路
boolean[][] used;
int target;
public int[][] floodfill(int[][] image, int sr, int sc, int color) {
int m = image.length,n = image[0].length;
used = new boolean[m][n];
target = image[sr][sc];
dfs(image,sr,sc,color);
return image;
}
public void dfs(int[][] image,int i,int j,int color){
int m = image.length,n = image[0].length;
//剪枝,越界直接返回
if(i < 0 || j < 0 || i >= m || j >= n){
return ;
}
//使用过的位置也直接返回
if(used[i][j]) return ;
if(image[i][j] == target){
//上下左右去深搜,符合条件的都标记为color
image[i][j] = color;
used[i][j] = true;
dfs(image,i - 1,j,color);
dfs(image,i + 1,j,color);
dfs(image,i,j - 1,color);
dfs(image,i,j + 1,color);
}
}
}解法二:基于解法一,我们可以通过定义两个数组来表示方向:dx[ ],dy[ ],其中dx[ ],dy[ ]的位置要一一对应,具体操作如下:
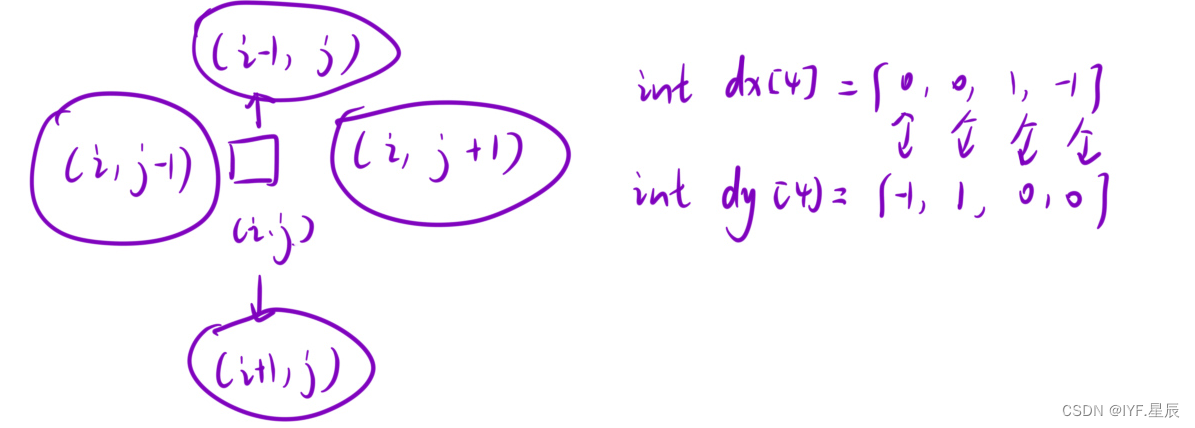
代码详解:
class solution {
boolean[][] used;
int target;
int[] dx = {-1,1,0,0};
int[] dy = {0,0,1,-1};
public int[][] floodfill(int[][] image, int sr, int sc, int color) {
int m = image.length,n = image[0].length;
used = new boolean[m][n];
target = image[sr][sc];
dfs(image,sr,sc,color);
return image;
}
public void dfs(int[][] image,int i,int j,int color){
int m = image.length,n = image[0].length;
//每次进入都进行标记,并将该位置值改为color
used[i][j] = true;
image[i][j] = color;
//相当于上下左右四个方向进行深搜
for(int k = 0;k < 4;k++){
int x = i + dx[k],y = j + dy[k];
//所有不符合条件的都不能进入深搜
if(x >= 0 && x < m && y >= 0 && y < n
&& !used[x][y] && image[x][y] == target){
dfs(image,x,y,color);
}
}
}
}运行结果:
二.岛屿数量:
- 题目链接:200. 岛屿数量 - 力扣(leetcode)
- 题目描述:
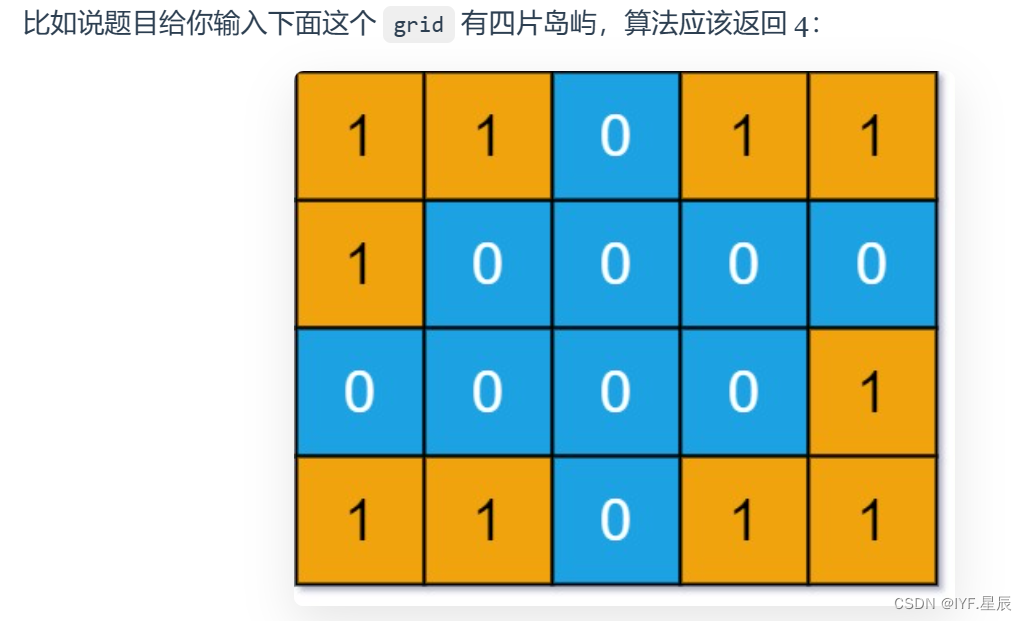
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。

- 对应函数签名如下:

代码详解:
解法一:与上面一样,两种解法(类似):
class solution {
int res = 0;
public int numislands(char[][] grid) {
int m = grid.length,n = grid[0].length;
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if(grid[i][j] == '1'){
//每次找到一个岛屿记录一下,再将这个岛屿淹没
res++;
dfs(grid,i,j);
}
}
}
return res;
}
public void dfs(char[][] grid,int i,int j){
int m = grid.length,n = grid[0].length;
//处理边界情况
if(i < 0 || j < 0 || i >= m || j >= n){
return ;
}
if(grid[i][j] == '0') return ;
grid[i][j] = '0';
//上下左右去淹没这个岛屿
dfs(grid,i - 1,j);
dfs(grid,i + 1,j);
dfs(grid,i,j - 1);
dfs(grid,i,j + 1);
}
}解法二:
class solution {
int res = 0;
int[] dx = {0,0,-1,1};
int[] dy = {1,-1,0,0};
public int numislands(char[][] grid) {
int m = grid.length,n = grid[0].length;
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if(grid[i][j] == '1'){
//说明找到「⼀个岛屿」,记录到最终结果 res⾥⾯
res++;
dfs(grid,i,j);//将这个岛屿淹没
}
}
}
return res;
}
public void dfs(char[][] grid,int i,int j){
int m = grid.length,n = grid[0].length;
grid[i][j] = '0';
for(int k = 0;k < 4;k++){
int x = i + dx[k],y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n
&& grid[x][y] != '0'){
dfs(grid,x,y);
}
}
}
}运行结果:
三.岛屿的最大面积:
- 题目链接:695. 岛屿的最大面积 - 力扣(leetcode)
- 题目描述:
给你一个大小为
m x n的二进制矩阵grid。岛屿 是由一些相邻的
1(代表土地) 构成的组合,这里的「相邻」要求两个1必须在 水平或者竖直的四个方向上 相邻。你可以假设grid的四个边缘都被0(代表水)包围着。岛屿的面积是岛上值为
1的单元格的数目。计算并返回
grid中最大的岛屿面积。如果没有岛屿,则返回面积为0

- 对应函数签名:

代码详解:
解法一:
class solution {
int maxarea = 0;
int count;
boolean[][] used;
public int maxareaofisland(int[][] grid) {
int m = grid.length,n = grid[0].length;
used = new boolean[m][n];
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if(grid[i][j] == 1){
//每次找到一个岛屿都要重置计数
count = 0;
dfs(grid,i,j);
maxarea = math.max(maxarea,count);
}
}
}
return maxarea;
}
public void dfs(int[][] grid,int i,int j){
int m = grid.length,n = grid[0].length;
//处理边界情况
if(i < 0 || j < 0 || i >= m || j >= n){
return ;
}
if(grid[i][j] == 0) return ;
if(used[i][j]) return ;
used[i][j] = true;
count++;
dfs(grid,i - 1,j);
dfs(grid,i + 1,j);
dfs(grid,i,j - 1);
dfs(grid,i,j + 1);
}
}解法二:
class solution {
int maxarea = 0;
int count = 0;
int[] dx = {0,0,-1,1};
int[] dy = {1,-1,0,0};
boolean[][] used;
public int maxareaofisland(int[][] grid) {
int m = grid.length,n = grid[0].length;
used = new boolean[m][n];
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if(grid[i][j] == 1){
//每次找到一个岛屿都要重置计数
count = 0;
dfs(grid,i,j);
maxarea = math.max(maxarea,count);
}
}
}
return maxarea;
}
public void dfs(int[][] grid,int i,int j){
int m = grid.length,n = grid[0].length;
used[i][j] = true;
count++;
for(int k = 0;k < 4;k++){
int x = i + dx[k],y = j + dy[k];
//处理不满足条件的情况
if(x >= 0 && x < m && y >= 0 && y < n
&& !used[x][y] && grid[x][y] != 0){
dfs(grid,x,y);
}
}
}
}运行结果:

四.被围绕的区域:
- 题目链接:130. 被围绕的区域 - 力扣(leetcode)
- 题目描述:给你一个
m x n的矩阵board,由若干字符'x'和'o',找到所有被'x'围绕的区域,并将这些区域里所有的'o'用'x'填充。

- 对应函数签名:


代码详解:
class solution {
boolean[][] used;
public void solve(char[][] board) {
int m = board.length,n = board[0].length;
used = new boolean[m][n];
//分别对应上下左右,标记外围的'o'
for(int i = 0;i < n;i++){
dfs2(board,0,i);
dfs2(board,m - 1,i);
}
for(int j = 0;j < m;j++){
dfs2(board,j,0);
dfs2(board,j,n - 1);
}
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if(board[i][j] != 'x' && !used[i][j]){
dfs(board,i,j);
}
}
}
}
//将内部的'o'全部标记为'x'
public void dfs(char[][] board,int i,int j){
int m = board.length,n = board[0].length;
if(i < 0 || j < 0 || i >= m || j >= n){
return ;
}
if(board[i][j] == 'x') return;
if(used[i][j]) return ;
used[i][j] = true;
board[i][j] = 'x';
dfs(board,i - 1,j);
dfs(board,i + 1,j);
dfs(board,i,j - 1);
dfs(board,i,j + 1);
}
//将外围的位置标记为true,后续不会对其进行操作
public void dfs2(char[][] board,int i,int j){
int m = board.length,n = board[0].length;
if(i < 0 || j < 0 || i >= m || j >= n){
return ;
}
if(board[i][j] == 'x') return;
if(used[i][j]) return ;
used[i][j] = true;
dfs2(board,i - 1,j);
dfs2(board,i + 1,j);
dfs2(board,i,j - 1);
dfs2(board,i,j + 1);
}
}运行结果:

五.太平洋大西洋水流问题:
- 题目链接:417. 太平洋大西洋水流问题 - 力扣(leetcode)
- 题目描述:
有一个 m × n 的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。
这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights , heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。
岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。
返回网格坐标 result 的 2d 列表 ,其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

- 对应函数标签:


代码详解:
class solution {
int m ,n;
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
public list<list<integer>> pacificatlantic(int[][] heights) {
m = heights.length;
n = heights[0].length;
boolean[][] pac = new boolean[m][n];
boolean[][] atl = new boolean[m][n];
//先搞太平洋
for(int j = 0;j < n;j++) dfs(heights,0,j,pac);
for(int i = 0;i < m;i++) dfs(heights,i,0,pac);
//在搞大西洋
for(int i = 0;i < m;i++) dfs(heights,i,n - 1,atl);
for(int j = 0;j < n;j++) dfs(heights,m - 1,j,atl);
//再提取结果:
list<list<integer>> res = new arraylist<>();
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if(pac[i][j] && atl[i][j]){
list<integer> temp = new arraylist<>();
temp.add(i);temp.add(j);
res.add(temp);
}
}
}
return res;
}
public void dfs(int[][] heights,int i,int j,boolean[][] used){
used[i][j] = true;
for(int k = 0;k < 4;k++){
int x = i + dx[k],y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n
&& !used[x][y] && heights[x][y] >= heights[i][j]){
dfs(heights,x,y,used);
}
}
}
}运行结果:

结语: 写博客不仅仅是为了分享学习经历,同时这也有利于我巩固知识点,总结该知识点,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进。同时也希望读者们不吝啬你们的点赞+收藏+关注,你们的鼓励是我创作的最大动力!






发表评论