前言
这篇都是关于贪心算法的oj题,但是并不只有这一种方法,但在本篇中只写出贪心的解法,标题下面都有超链接,可以同时过去写题哦~
之后还会更新相关专题的,敬请期待!!
算法解释
📍455. 分发饼干

解题思路
因为饥饿度最小的孩子最容易吃饱,所以我们先考虑这个孩子。为了尽量使得剩下的饼干可以满足饥饿度更大的孩子,所以我们应该把大于等于这个孩子饥饿度的、且大小最小的饼干给这个孩子。满足了这个孩子之后,我们采取同样的策略,考虑剩下孩子里饥饿度最小的孩子,直到没有满足条件的饼干存在。
简而言之,这里的贪心策略是,给剩余孩子里最小饥饿度的孩子分配最小的能饱腹的饼干。
至于具体实现,因为我们需要获得大小关系,一个便捷的方法就是把孩子和饼干分别排序。这样我们就可以从饥饿度最小的孩子和大小最小的饼干出发,计算有多少个对子可以满足条件。
注意:对数组或字符串排序是常见的操作,方便之后的大小比较。
注意:在之后的讲解中,若我们谈论的是对连续空间的变量进行操作,我们并不会明确区分数组和字符串,因为它们本质上都是在连续空间上的有序变量集合。一个字符串“abc”可以被看作一个数组 [‘a’,‘b’,‘c’]。
ac代码
class solution {
public:
int findcontentchildren(vector<int>& g, vector<int>& s) {
sort(g.begin(),g.end());
sort(s.begin(),s.end());
int child=0,cookie=0;
while(child<g.size()&&cookie<s.size())
{
if(g[child] <= s[cookie]) ++child;
++cookie;
}
return child;
}
};
📍435. 无重叠区间

解题思路
在选择要保留区间时,区间的结尾十分重要:选择的区间结尾越小,余留给其它区间的空间就越大,就越能保留更多的区间。因此,我们采取的贪心策略为,优先保留结尾小且不相交的区间。
具体实现方法为,先把区间按照结尾的大小进行增序排序,每次选择结尾最小且和前一个选择的区间不重叠的区间。我们这里使用 c++ 的 lambda,结合 std::sort() 函数进行自定义排序。
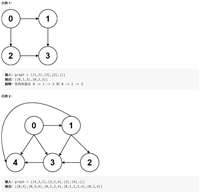
在样例中,排序后的数组为 [[1,2], [1,3], [2,4]]。按照我们的贪心策略,首先初始化为区间[1,2];由于 [1,3] 与 [1,2] 相交,我们跳过该区间;由于 [2,4] 与 [1,2] 不相交,我们将其保留。因此最终保留的区间为 [[1,2], [2,4]]。
ac代码
class solution {
public:
int eraseoverlapintervals(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end(), [](vector<int>& a, vector<int>& b) {
return a[1] < b[1];
});
int total = 0, prev = intervals[0][1];
for (int i = 1; i < intervals.size(); ++i) {
if (intervals[i][0] < prev) {
++total;
} else {
prev = intervals[i][1];
}
}
return total;
}
};
📍605. 种花问题

解题思路
从左向右遍历花坛,在可以种花的地方就种一朵,能种就种(因为在任一种花时候,不种都不会得到更优解),就是一种贪心的思想 这里可以种花的条件是:
自己为空
左边为空 或者 自己是最左
右边为空 或者 自己是最右
最后判断n朵花是否有剩余,为了效率起见,可以在种花的过程中做判断,一旦花被种完就返回true
ac代码
class solution {
public:
bool canplaceflowers(vector<int>& flowerbed, int n) {
for(int i=0;i<flowerbed.size();++i)
{
if(flowerbed[i]==0&&(i==0||flowerbed[i-1]==0)&&(i==flowerbed.size()-1||flowerbed[i+1]==0))
{
n--;
if(n<=0)return true;
flowerbed[i]=1;
}
}
return n<=0;
}
};
📍452. 用最少数量的箭引爆气球

解题思路
- 这题和435题有异曲同工之妙
- 注意它是垂直x轴射箭
- 和435题思路相似,先按右边界升序排列
- 排列好以后,拿出第一个区间的右边界
- 循环遍历后面的区间的左边界
- 如果左边界大于前一个区间的右边界
- 就加1,然后将pos设置为这个区间的右边界
总之:
我想让当前区间尽可能重合更多区间,而且希望这些区间,内部互相都重合。
即我想追求遍历时重合的连续性。基于当前区间右端这个参照物,b 的重合带来一层限制,右端递增带来另一层限制,二者共同保证了 a、b 的重合。
当前区间 -----r
区间a ---------r
区间b l-------
ac代码
class solution {
public:
int findminarrowshots(vector<vector<int>>& points) {
if(points.empty())return 0;
sort(points.begin(),points.end(),[](const vector<int>&u,const vector<int>&v){
return u[1]<v[1]
});
int pos=points[0][1];
int ans=1;
for(const vector<int>&ball:points)
{
if(ball[0]>pos)
{
pos=ball[1];
++ans;
}
}
return ans;
}
};
📍763. 划分字母区间

解题思路
- 这题也是使用贪心算法
- 在做一些贪心算法的题时预处理一下会让代码变得更优美
- 这题要分成更多的片段,但是同样的字符只能在同一个片段中
- 预处理:将每一个字符的最后位置记录下来
- 设置start、end记录字段串的起始终止位置
- 再遍历一遍字符串,如果某个字符的最后位置大于当前end
- end=那个字符的最后位置
- 直到 i 等于end说明字符找到了结尾
ac代码
class solution {
public:
vector<int> partitionlabels(string s) {
int last[26];
int length = s.size();
for (int i = 0; i < length; i++) {
last[s[i] - 'a'] = i;
}
vector<int> partition;
int start = 0, end = 0;
for (int i = 0; i < length; i++) {
end = max(end, last[s[i] - 'a']);
if (i == end) {
partition.push_back(end - start + 1);
start = end + 1;
}
}
return partition;
}
};
📍121. 买卖股票的最佳时机

解题思路
- 只需要考虑最低的花费和最高的利润
- 最低的花费是在当天的价格中选择最低的
- 利润就需要考虑今天的价格 - 当前最低利润
- 然后取最大利润
ac代码
class solution {
public:
int maxprofit(vector<int>& prices) {
int cost=int_max;
int profit=0;
for(auto price:prices)
{
cost=min(cost,price);
profit=max(profit,price-cost);
}
return profit;
}
};
📍122. 买卖股票的最佳时机 ii

解题思路
- 这题和上一题不同,它的要求是一只股票,不管你什么时候卖,求最大利润
- 只需要在低点买,高点卖即可
ac代码
class solution {
public:
int maxprofit(vector<int>& prices) {
int profit=0;
for(int i=1;i<prices.size();++i)
{
if(prices[i]-prices[i-1]>0)profit+=prices[i]-prices[i-1];
}
return profit;
}
};
📍406. 根据身高重建队列

解题思路
-
[h,k],h是身高看得懂。问题是为毛k这个数这么奇怪。是不是!
-
试着理解一下,k代表的是,现在这个队里,自己前面的人里面,h比自己大或与自己相等的人-的个数。
-
好比[7,1],代表,自己高7,排在自己前面,且比自己高或相等的只有一个人。
-
而[7,0]意思是,排在自己前面的人,没有比自己高的
ac代码:
class solution {
public:
vector<vector<int>> reconstructqueue(vector<vector<int>>& people) {
sort(people.begin(),people.end(),[](const vector<int>&u,const vector<int>&v){
return u[0]>v[0] || (u[0]==v[0]&&u[1]<v[1]);
});
vector<vector<int>> ans;
for(auto& person : people)
{
ans.insert(ans.begin()+person[1],person);
}
return ans;
}
};
📍665. 非递减数列

解题思路
思路来自:@码不停题
大佬思路出生入化
这道题给了我们一个数组,说我们最多有1次修改某个数字的机会,
问能不能将数组变为非递减数组。题目中给的例子太少,不能覆盖所有情况,我们再来看下面三个例子:
4,2,3
-1,4,2,3
2,3,3,2,4
我们通过分析上面三个例子可以发现,当我们发现后面的数字小于前面的数字产生冲突后,
[1]有时候需要修改前面较大的数字(比如前两个例子需要修改4),
[2]有时候却要修改后面较小的那个数字(比如前第三个例子需要修改2),
那么有什么内在规律吗?是有的,判断修改那个数字其实跟再前面一个数的大小有关系,
首先如果在前面的数不存在,比如例子1,4前面没有数字了,我们直接修改前面的数字为当前的数字2即可。
而当再前面的数字存在,并且小于当前数时,比如例子2,-1小于2,我们还是需要修改前面的数字4为当前数字2;
如果再前面的数大于当前数,比如例子3,3大于2,我们需要修改当前数2为前面的数3。
ac代码
class solution {
public:
bool checkpossibility(vector<int>& nums) {
int count=0;
for(int i=1;i<nums.size();++i)
{
if(nums[i-1]>nums[i])
{
count++;
if(i-1==0)nums[i-1]=nums[i];
else if(i>=2&&nums[i-2]<nums[i])nums[i-1]=nums[i];
else if(nums[i-2]>nums[i])nums[i]=nums[i-1];
}
if(count>1)return false;
}
return true;
}
};

发表评论