lcp 07. 传递信息
小朋友 a 在和 ta 的小伙伴们玩传信息游戏,游戏规则如下:
有 n 名玩家,所有玩家编号分别为 0 ~ n-1,其中小朋友 a 的编号为 0
每个玩家都有固定的若干个可传信息的其他玩家(也可能没有)。传信息的关系是单向的(比如 a 可以向 b 传信息,但 b 不能向 a 传信息)。
每轮信息必须需要传递给另一个人,且信息可重复经过同一个人
给定总玩家数 n,以及按 [玩家编号,对应可传递玩家编号] 关系组成的二维数组 relation。返回信息从小 a (编号 0 ) 经过 k 轮传递到编号为 n-1 的小伙伴处的方案数;若不能到达,返回 0。
示例 1:
输入:n = 5, relation = [[0,2],[2,1],[3,4],[2,3],[1,4],[2,0],[0,4]], k = 3
输出:3
解释:信息从小 a 编号 0 处开始,经 3 轮传递,到达编号 4。共有 3 种方案,分别是 0->2->0->4, 0->2->1->4, 0->2->3->4。
示例 2:
输入:n = 3, relation = [[0,2],[2,1]], k = 2
输出:0
解释:信息不能从小 a 处经过 2 轮传递到编号 2
限制:
2 <= n <= 10
1 <= k <= 5
1 <= relation.length <= 90, 且 relation[i].length == 2
0 <= relation[i][0],relation[i][1] < n 且 relation[i][0] != relation[i][1]
主要思路:
- 数据结构的选择,因为涉及到了一对多的键值映射,因此选择multimap这个数据结构;
- 对于有多少种选择这种问题,利用dfs进行遍历,同时,利用题目限制的路径长度k,及时返回;
代码如下:
#include <vector>
#include <map>
#include <iostream>
using namespace std;
class solution
{
private:
multimap<int, int> mp;
int res = 0, m_n, m_k;
void dfs(int src, int deep)
{
if (deep == m_k)
{
if (src == m_n - 1)
{
res++;
}
return;
}
for (auto it = mp.lower_bound(src); it != mp.upper_bound(src); it++)
{
dfs(it->second, deep + 1);
}
return;
}
public:
int numways(int n, vector<vector<int>> &relation, int k)
{
m_n = n, m_k = k;
for (int i = 0; i < relation.size(); i++)
{
mp.insert(make_pair(relation[i][0], relation[i][1]));
}
dfs(0, 0);
return res;
}
};
int main()
{
solution sol;
vector<vector<int>> relations = {{0, 2}, {2, 1}};
int res = sol.numways(3, relations, 2);
cout << res;
return 0;
}
关于multimap这个stl的使用及原理,在此做一点补充:
lcp 05. 发 leetcoin
力扣决定给一个刷题团队发leetcoin作为奖励。同时,为了监控给大家发了多少leetcoin,力扣有时候也会进行查询。
该刷题团队的管理模式可以用一棵树表示:
团队只有一个负责人,编号为1。除了该负责人外,每个人有且仅有一个领导(负责人没有领导);
不存在循环管理的情况,如a管理b,b管理c,c管理a。
力扣想进行的操作有以下三种:
给团队的一个成员(也可以是负责人)发一定数量的leetcoin;
给团队的一个成员(也可以是负责人),以及他/她管理的所有人(即他/她的下属、他/她下属的下属,……),发一定数量的leetcoin;
查询某一个成员(也可以是负责人),以及他/她管理的所有人被发到的leetcoin之和。
输入:
n表示团队成员的个数(编号为1~n,负责人为1);
leadership是大小为(n - 1) * 2的二维数组,其中每个元素[a, b]代表b是a的下属;
operations是一个长度为q的二维数组,代表以时间排序的操作,格式如下:
operations[i][0] = 1: 代表第一种操作,operations[i][1]代表成员的编号,operations[i][2]代表leetcoin的数量;
operations[i][0] = 2: 代表第二种操作,operations[i][1]代表成员的编号,operations[i][2]代表leetcoin的数量;
operations[i][0] = 3: 代表第三种操作,operations[i][1]代表成员的编号;
输出:
返回一个数组,数组里是每次查询的返回值(发leetcoin的操作不需要任何返回值)。由于发的leetcoin很多,请把每次查询的结果模1e9+7 (1000000007)。
示例 1:
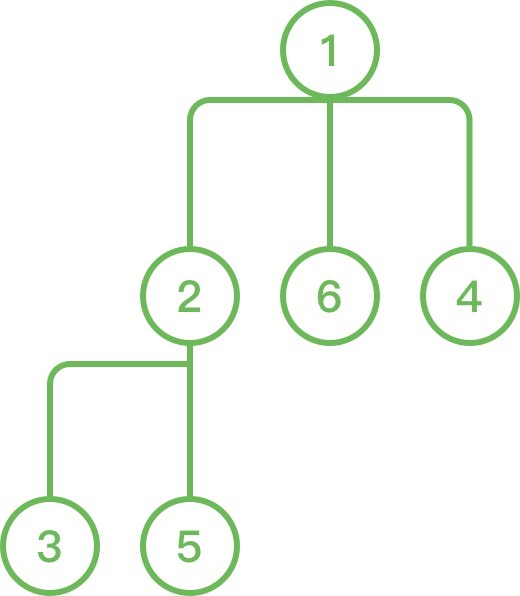
输入:n = 6, leadership = [[1, 2], [1, 6], [2, 3], [2, 5], [1, 4]], operations = [[1, 1, 500], [2, 2, 50], [3, 1], [2, 6, 15], [3, 1]]
输出:[650, 665]
解释:团队的管理关系见下图。
第一次查询时,每个成员得到的leetcoin的数量分别为(按编号顺序):500, 50, 50, 0, 50, 0;
第二次查询时,每个成员得到的leetcoin的数量分别为(按编号顺序):500, 50, 50, 0, 50, 15.
限制:
1 <= n <= 50000
1 <= q <= 50000
operations[i][0] != 3 时,1 <= operations[i][2] <= 5000
这道题是lcp的hard题目,应该属于力扣的天花板题目了,需要用线段树来求解。这种数据结构比较复杂,对于非acm选手并不是很友好,自己也是参照着题解1强行写了一波,写的太勉强了,就算是当作线段树的一个初步了解吧。
oi wiki总结的线段树部分很全面:https://oi-wiki.org/ds/seg/.
p.s. 自己总是喜欢挑战一下,但这次挑战下来花费的时间太多了,远远超过了自己给刷题留下的预期时间,得不偿失,这道题的难度也远超过了自己的能力范围,下次还是避一下lcp的hard题目吧,毕竟现在的主要任务不是联系oj。
class solution
{
public:
static constexpr int max_n = 50000 + 5;
static constexpr int p = int(1e9) + 7;
vector<int> g[max_n];
int sz[max_n], p, dfsorder[max_n], id[max_n];
long long sum[max_n * 4], tag[max_n * 4];
int dfsgetorder(int o)
{
dfsorder[++p] = o;
id[o] = p;
for (const auto &x : g[o])
{
sz[o] += dfsgetorder(x);
}
return ++sz[o];
}
inline int ls(int o)
{
return o << 1;
}
inline int rs(int o)
{
return o << 1 | 1;
}
inline void pushdown(int o, int l, int r)
{
if (!tag[o])
return;
int mid = (l + r) >> 1;
tag[ls(o)] += tag[o];
tag[rs(o)] += tag[o];
sum[ls(o)] += tag[o] * (mid - l + 1);
sum[rs(o)] += tag[o] * (r - mid);
tag[o] = 0;
}
inline void pushup(int o)
{
sum[o] = sum[ls(o)] + sum[rs(o)];
}
void update(int o, int l, int r, int l, int r, int v)
{
// l,r是线段树范围;l, r是更新范围;
if (l <= l && r <= r)
{
tag[o] += v;
sum[o] += v * (r - l + 1);
return;
}
int mid = (l + r) >> 1;
pushdown(o, l, r);
if (l <= mid)
update(ls(o), l, mid, l, r, v);
if (r > mid)
update(rs(o), mid + 1, r, l, r, v);
pushup(o);
}
long long query(int o, int l, int r, int l, int r)
{
if (l <= l && r <= r)
{
return sum[o];
}
long long ret = 0;
int mid = (l + r) >> 1;
pushdown(o, l, r);
if (l <= mid)
ret += query(ls(o), l, mid, l, r);
if (r > mid)
ret += query(rs(o), mid + 1, r, l, r);
return ret;
}
vector<int> bonus(int n, vector<vector<int>> &leadership, vector<vector<int>> &operations)
{
for (const auto &v : leadership)
{
g[v[0]].push_back(v[1]);
}
fill(sz + 1, sz + n + 1, 0);
this->p = 0;
dfsgetorder(1);
memset(sum, 0, sizeof sum);
memset(tag, 0, sizeof tag);
vector<int> ans;
for (const auto &v : operations)
{
if (v[0] == 1)
{
update(1, 1, n, id[v[1]], id[v[1]], v[2]);
}
else if (v[0] == 2)
{
update(1, 1, n, id[v[1]], id[v[1]] + sz[v[1]] - 1, v[2]);
}
else
{
ans.push_back(query(1, 1, n, id[v[1]], id[v[1]] + sz[v[1]] - 1) % p);
}
}
return ans;
}
};
27. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 o(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝
int len = removeelement(nums, val);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,3,0,4]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
提示:
0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100
利用双指针的思路,头指针从前往后遍历元素,尾指针表示索引最大的值不等于val的元素位置,结束的条件就是头指针大于等于尾指针了,代码如下:
#include <vector>
#include <iostream>
using namespace std;
class solution
{
public:
int removeelement(vector<int> &nums, int val)
{
int tail = nums.size() - 1;
while (tail >= 0 && nums[tail] == val)
{
tail--;
}
for (int i = 0; i < tail; i++)
{
if (nums[i] == val)
{
swap(nums[i], nums[tail]);
while (tail > i && nums[tail] == val)
{
tail--;
}
}
}
return tail + 1;
}
};
int main()
{
solution sol;
vector<int> nums = {2, 2, 2, 2, 2, 2};
int val = 2;
int res = sol.removeelement(nums, val);
for (int i = 0; i < res; i++)
{
cout << nums[i] << " ";
}
return 0;
}
45. 跳跃游戏 ii
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
1 <= nums.length <= 104
0 <= nums[i] <= 1000
题目保证可以到达 nums[n-1]
自己一开始是把这道题目当成了动态规划来做,代码如下:
class solution
{
public:
int jump(vector<int> &nums)
{
int n = nums.size();
vector<int> numjump(n, 0);
for (int i = 0; i < n; i++)
{
for (int j = i + 1; j <= min(i + nums[i], n - 1); j++)
{
numjump[j] = numjump[j] == 0 ? numjump[i] + 1 : min(numjump[j], numjump[i] + 1);
}
}
return numjump[n - 1];
}
};
提交后,发现时间复杂度较低,在力扣只打败了6%左右的提交。
于是进一步参考了题解,发现题解是利用贪心算法来做的,代码如下:
class solution
{
public:
int jump(vector<int> &nums)
{
int n = nums.size();
int maxpos = 0; // 下一步可以到达的最远距离
int end = 0; // 当前步数,可以到达的最远距离
int step = 0; // 当前步数
for (int i = 0; i < n; i++)
{
if (i <= maxpos) // 判断是否可以到达
{
if (i > end)
{
end = maxpos;
step++;
}
maxpos = max(maxpos, i + nums[i]);
}
else
{
break;
}
}
if (maxpos >= n - 1)
{
return step;
}
else // 不可以到达,返回-1
{
return -1;
}
}
};
https://leetcode.cn/problems/coin-bonus/solutions/2477616/fa-leetcoin-by-leetcode-solution-i2zm/ ↩︎




发表评论