【算法】一文搞懂归并排序_算法

概念

归并排序利用了分治思想，将待排序的数组范围层层划分，每次划分会得到两个大小相近的区间。当无法划分时，递归结束，自下而上进行区间合并merge操作，合并操作依次比较两个区间的元素，进而使合并后的区间有序。当进行到最后一次合并区间时，我们将会得到目标范围的有序序列。这个过程如图所示。

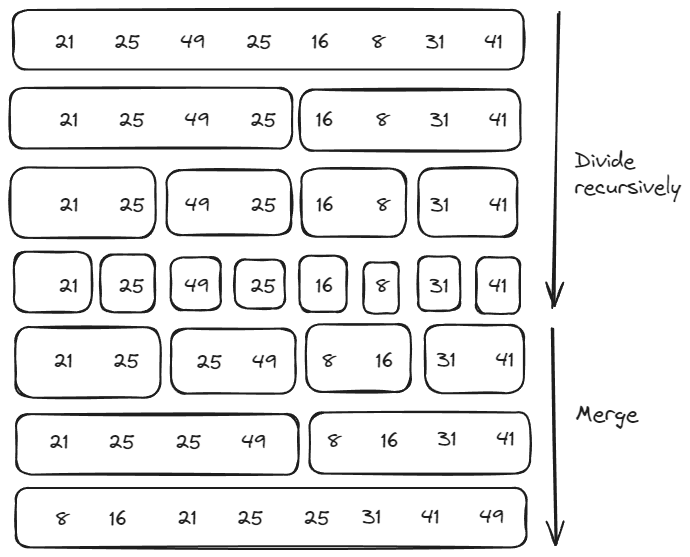
在这里插入图片描述

由于归并排序并不是基于交换的排序算法，因此没办法做到原地in-place排序，而是需要借助一个辅助数组，以便在合并时，可以暂时存放左侧区间的元素，这样可以将经过比较得到的元素直接放入原数组的正确位置。这也是归并排序空间复杂度的主要来源。

此外，归并排序是一种稳定的排序算法。需要注意的是，在合并过程中，左区间的元素在原数组中的位置总是位于右区间元素的左边。因此，当比较两个区间的当前元素时，如果左区间的元素小于或等于右区间的元素，应优先选择左区间的元素放入结果数组。这样可以保证相等元素的相对顺序不变，从而维护算法的稳定性。(切忌漏掉等于)

递归实现

inline void merge(int *arr, int *aux, const int left, const int mid, const int right) {
    for (int i = left; i < mid + 1; ++i) {
        aux[i] = arr[i];  // * 为避免冗余拷贝，此处先将左区间移至辅助数组
                          // * 排序时直接向arr写入数据即可，而不用最后冗余执行拷贝
    }
    int s1 = left, s2 = mid + 1, k = left;
    while (s1 <= mid && s2 <= right) {
        if (aux[s1] <= arr[s2]) { // * 请注意，为了保持排序算法稳定，这里应该是小于等于
            arr[k++] = aux[s1++];
        } else {
            arr[k++] = arr[s2++];
        }
    }
    while (s1 <= mid) {
        arr[k++] = aux[s1++];
    }
    while (s2 <= right) {
        arr[k++] = arr[s2++];
    }
}

// * 递归版本-归并排序
// * 排序区间：[left, right)
void mergesort(int *arr, int *aux, const int left, const int right) {
    if (left >= right)
        return;
    const int mid = (left + right) / 2;
    mergesort(arr, aux, left, mid);
    mergesort(arr, aux, mid + 1, right);
    merge(arr, aux, left, mid, right);
}

非递归实现

// * 迭代版本-归并排序
void mergesort2(int *arr, int n) {
    int *aux = new int[n];
    for (int step = 1; step < n; step *= 2) { // 以循环的形式，用指针控制区间划分，逐一区间进行合并，区间范围依次倍增
        for (int i = 0; i < n - 1; i += step * 2) {
            int left = i, mid = i + step - 1, right = min(i + 2 * step - 1, n - 1);
            merge(arr, aux, left, mid, right);
        }
    }
    delete[] aux;
}

复杂度分析

时间复杂度：递归划分深度为 $o (l g n)$ ，合并每一层的时间复杂度为 $o (n)$ ，因此总时间为 $o (n l g n)$ 。
空间复杂度： $o (n)$ ，辅助空间必不可少。

技巧应用

lcr 170. 交易逆序对的总数 - 力扣（leetcode）

在归并排序的每一次merge操作时，我们有两个指针s1和s2分别指向待合并的左右两个区间中的元素，且这两个区间的数据有两个特点，即左区间的数在原数组中一定在右区间的左侧，且左右两区间的数据各自是有序的。因此，当归并进行到arr[s1]小于arr[s2]时，假设左区间为[l, m]，那么arr[s1]一定和右区间中s2及其左侧元素均构成逆序对，这个逆序对的数量为m - s1 + 1，最后我们在递归过程中将这些逆序对数目收集起来即可。

示例代码如下：

// 归并排序解法
class solution {
private:
    int mergesort(vector<int>& record, vector<int> &aux, int l, int r) {
        if (l >= r) return 0;
        int m = (l + r) / 2;
        // 递归
        int rtn = mergesort(record, aux, l, m) + mergesort(record, aux, m + 1, r);
        for (int i = l; i <= m; ++i) {
            aux[i] = record[i];
        }
        int s1 = l, s2 = m + 1, k = l;
        // 合并阶段
        while (s1 <= m && s2 <= r) {
            if (aux[s1] <= record[s2]){
                record[k++] = aux[s1++];
            } else {
                rtn += m - s1 + 1; // 统计逆序对数目
                record[k++] = record[s2++];
            }
        }
        while (s1 <= m) {
            record[k++] = aux[s1++];
        }
        while (s2 <= r) {
            record[k++] = record[s2++];
        }
        return rtn;
    }
public:
    int reversepairs(vector<int>& record) {
        if(record.empty()) return 0;
        vector<int> aux(record.size(), 0);
        return mergesort(record, aux, 0, record.size() - 1);
    }
};