决策树 数模打卡

决策树

1. 基本流程

一系列决策结果得到最终结论，每个测试的结果或是导出最终结论，或是导出进一步地判定问题。
决策树的叶结点对应决策结果，其他每个节点对应于一个属性测试；每个结点包含的样本集合根据属性测试的结果被划分到子结点中；根结点包含样本全集。
决策树学习：产生处理未见示例能力强的决策树。
递归生成决策树的算法：

• 当前接电所有样本同类，无需划分；
• 当前结点属性集为空 or 所有样本在宿友属性上取值相同，无法划分 -> 将当前结点标记为叶结点，并将类别设为所含样本最多的类别（当前结点的后验分布）；
• 当前样本集为空，不能划分 -> 将其类别设定为父结点所含样本最多的类别（父结点作为先验分布）。
  

2. 划分选择

上图第八行要选择最优划分属性。

2.1 信息增益

信息熵：度量样本集合纯度的指标。若当前样本集合d中第k类样本占比p_k，则d的信息熵定义为$$ent(d)=-\sum _{k=1}^{|y|}{p}_k{\log }_2{p}_k$$信息熵越小，d的纯度越高。
对于离散属性a，设有v个取值，第v个分支结点记为d^v，包含所有在a上取a^v的样本。计算出d^v的信息熵，并按样本数赋权重，计算出用属性a对样本集d进行划分所得的信息增益：$$gain(d,a)=ent(d)-\sum _{v=1}^v\frac{|d^v|}{|d|}ent(d^v).$$信息增益越大，意味着使用属性a来进行划分所获得的“纯度提升”越大。
故可以选择属性$a_{\ast }=\underset{a\in a}{\mathrm{argmax}}gain(d,a).$

2.2 增益率

信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好的不利影响，c4.5决策树算法选择“增益率”来选择最优划分属性。增益率定义为$$\begin{gathered} gain\_ratio(d,a)=\frac{gain(d,a)}{iv(a)} \\ 固有值iv(a)=-\sum _{v=1}^v\frac{|d^v|}{|d|}{\log }_2\frac{|d^v|}{|d|} \end{gathered}$$c4.5算法：先从候选划分属性中找出信息增益高于平均水平的属性，再选增益率最高的。

2.3 基尼指数

cart决策树用“基尼指数”选择划分属性，它反映了从数据集中随机抽取两个样本，其类别标记不一致的概率；数据集的纯度可以用基尼值来度量，基尼值越小，数据集纯度越高。$$gini(d)=\sum _{k=1}^{|y|}\sum _{k^{\prime }\ne k}{p}_k{p}_{k^{\prime }}=1-\sum _{k=1}^{|y|}{p}_k^2.$$基尼指数定义为$$gin{i}_{i}ndex(d,a)=\sum _{v=1}^v\frac{|d_v|}{|d|}gini(d_v).$$从候选属性集合中选出划分后基尼指数最小的属性。

3. 剪枝处理

针对“过拟合”。两个基本策略：

• 预剪枝：在决策树生成过程中，对每个结点在划分前进行估计，若不能带来决策树泛化技能提升，则停止，并标为叶结点。
• 后剪枝：从训练集生成一棵完整的决策树，自下而上对内部结点进行考察，若对应子树替换为叶结点（结点包含子树的样本）能带来泛化性能提升，则替换。
• 泛化技能的评定参考模型评估章。

4. 连续与缺失值

4.1 连续值处理

可取值数目不再有限->连续属性离散化技术。
c4.5决策树算法采用二分法。对于样本集d和连续属性a，若a中d上出现n个不同取值，排序并二分，基于划分点t可将d分为子集d_t^-和d_t⁺。对于连续属性a，可考察包含n-1个元素的候选划分点集合t_a。
然后像离散属性值一样考察这些划分点。例如 g a i n ( d , a ) = max ⁡ t ∈ t a   g a i n ( d , a , t ) max ⁡ t ∈ t a   e n t ( d ) − ∑ λ ∈ { − , + } ∣ d t λ ∣ ∣ d ∣ e n t ( d t λ ) gain(d,a)=\max\limits_{t\in t_{a}}\ gain(d,a,t)\\\max\limits_{t\in t_{a}}\ ent(d)-\sum_{\lambda\in \{-,+\}}\frac{|d_{t}^{\lambda}|}{|d|}ent(d_{t}^{\lambda}) gain(d,a)=t∈ta​max​ gain(d,a,t)t∈ta​max​ ent(d)−λ∈{−,+}∑​∣d∣∣dtλ​∣​ent(dtλ​)

4.2 缺失值处理

• 如何在属性值缺失情况下选划分属性？
• 给定划分属性，若样本在此的值缺失，如何划分样本？

对于第一个问题，$d$表示d在a上没有缺失值的样本子集，则只能通过$d$来判断属性优劣。并定义$\rho$表示无缺失值样本占比，$p_k$表示无缺失值样本中第k类所占比例，$r_v$则表示无缺失值样本中取值a^v的样本占比。
推广信息增益的定义$$\begin{gathered} gain(d,a)=\rho \times gain(d,a)=\rho \times (ent(d)-\sum _{v=1}^v{r}_{v}ent(d^v)) \\ ent(d)=-\sum _{k=1}^{|y|}{p}_k{\log }_2{p}_k. \end{gathered}$$

4.5 多变量决策树

上述分类划分，如果将变量作为坐标轴，则分类边界都是平行于坐标轴的。
多变量决策树能够实现斜划分甚至更复杂划分。在此类决策树中，非叶结点不再是仅对某个属性，而是对属性的线性组合进行测试，i.e. 每个非叶结点是一个形如${\sum }_{i=1}^d{w}_i{a}_i=t$的线性分类器。多变量决策树意在建立一个合适的线性分类器，例如：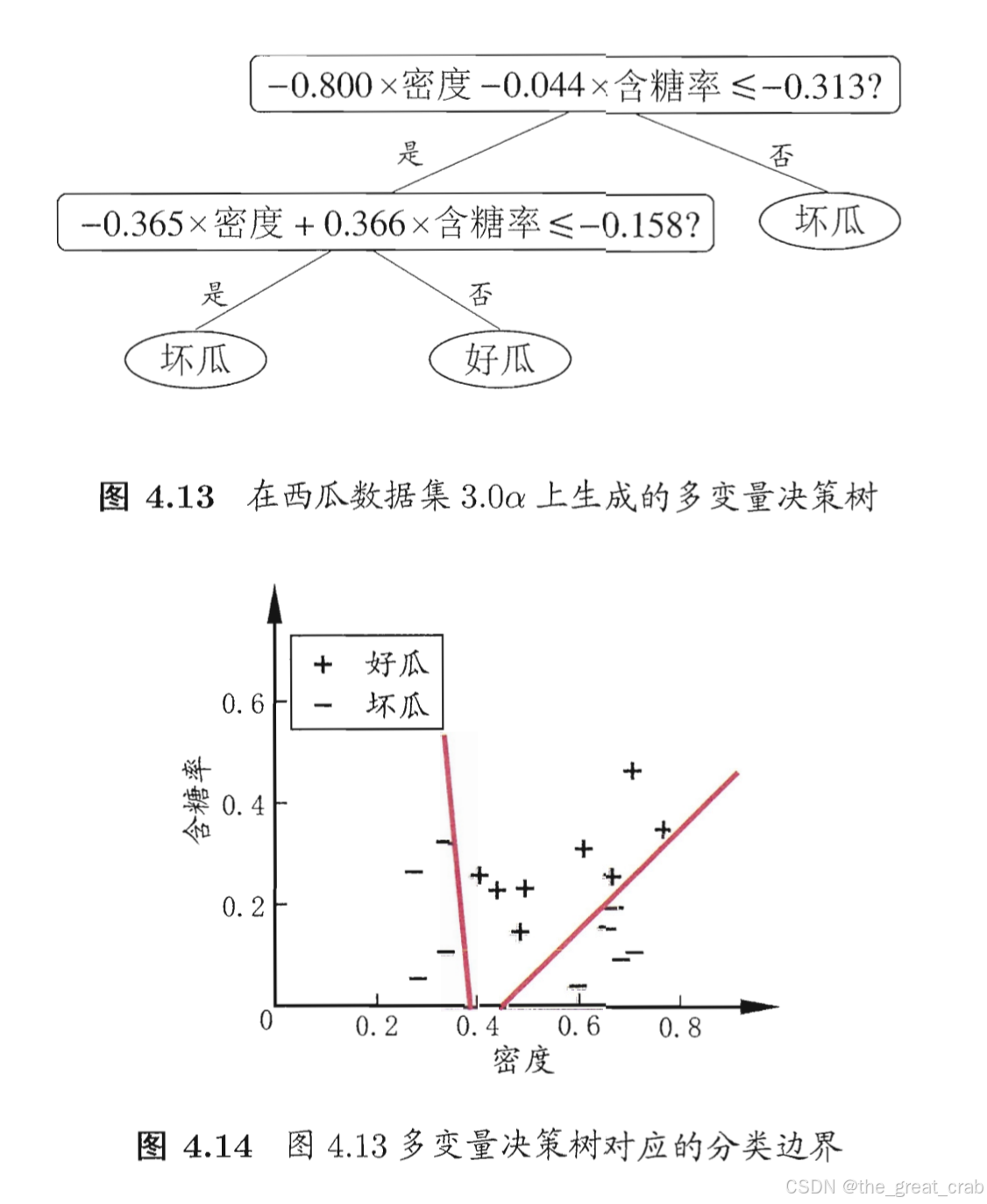
代码及运行结果（参考）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import standardscaler
from sklearn.tree import decisiontreeclassifier
from sklearn.metrics import accuracy_score, classification_report

# 加载数据集
path = "d:\\兹游奇绝\\没课\\数模打卡 7月\\titanic.csv"
data = pd.read_csv(path)

# 显示数据的前几行
print(data.head())

# 查看数据的详细信息
print(data.info())

# 确认数据集的列
print("数据集的列：", data.columns)

# 填充数值特征的缺失值
data["age"] = data["age"].fillna(data["age"].median())
data["fare"] = data["fare"].fillna(data["fare"].median())

# 对分类特征进行独热编码
data = pd.get_dummies(data, columns=["sex"], drop_first=true)

# 删除不需要的非数值特征
data.drop(columns=["name"], inplace=true)

# 分割数据为特征（x）和目标（y）
x = data.drop("survived", axis=1)
y = data["survived"]

# 将数据集分割为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)

# 特征标准化处理
scaler = standardscaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

# 创建决策树分类器并进行训练
model2 = decisiontreeclassifier(random_state=42)
model2.fit(x_train, y_train)

# 在测试数据上进行预测
y_pred = model2.predict(x_test)

# 计算准确性
accuracy = accuracy_score(y_test, y_pred)
print("模型准确性：", accuracy)

# 生成分类报告
report = classification_report(y_test, y_pred)
print("分类报告：\n", report)

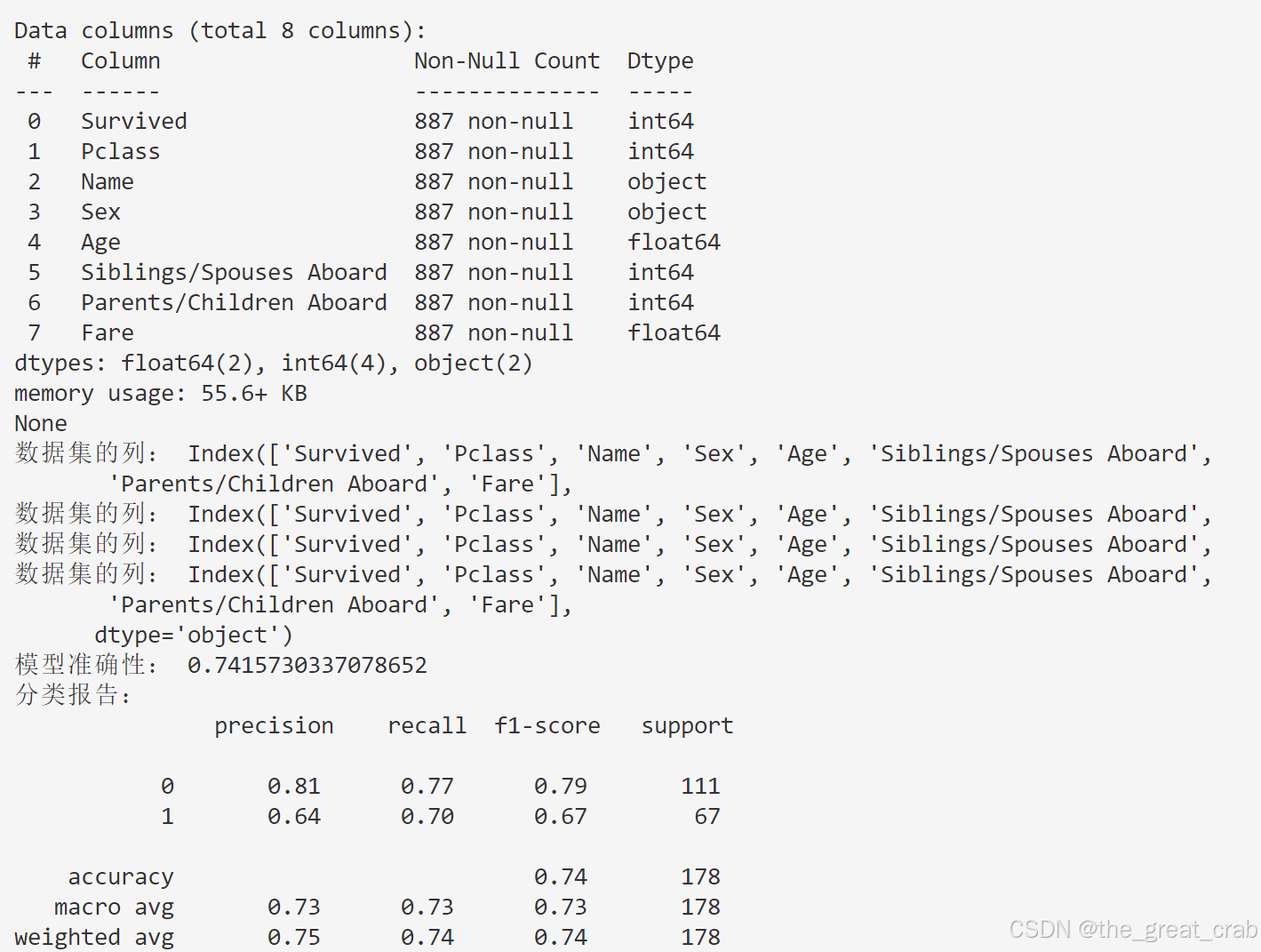
思考：为什么要标准化？

• 防止某些特征由于其较大的数值范围在模型训练中占主导地位，导致模型过于依赖某些特征。
• 可能有助于提高模型的收敛速度和稳定性。