【力扣 - 二叉树的中序遍历】

题目描述

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

提示：

树中节点数目在范围 [0, 100] 内

-100 <= node.val <= 100

方法一：递归

思路与算法

首先我们需要了解什么是二叉树的中序遍历：按照访问左子树——根节点——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程。

定义 inorder(root) 表示当前遍历到 root 节点的答案，那么按照定义，我们只要递归调用 inorder(root.left) 来遍历 root 节点的左子树，然后将 root 节点的值加入答案，再递归调用inorder(root.right) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。

代码

/**
 * definition for a binary tree node.
 */
struct treenode {
    int val;
    struct treenode *left;
    struct treenode *right;
};
/**
 * note: the returned array must be malloced, assume caller calls free().
 */
 /*
  * the  inorder  function performs an inorder traversal of a binary tree recursively. 
  * it stores the values of the nodes in the result array  res  and increments the size  ressize  accordingly. 
 */
 /*
  * the function "inorder" in the provided code is a recursive function. 
  * when a function calls itself inside its own definition, it is known as recursion. 
  * in this case, the "inorder" function is designed to perform an inorder traversal of a binary tree. 
  * 1. the "inorder" function is called with the root node of the binary tree.
  * 2. inside the function, it first checks if the current node is null. if it is null, the function returns and the recursion stops.
  * 3. if the current node is not null, the function recursively calls itself for the left child of the current node (root->left). this step continues until it reaches a null node (i.e., the left subtree is fully traversed).
  * 4. after traversing the left subtree, the function stores the value of the current node in the result array and increments the size of the result array.
  * 5. finally, the function recursively calls itself for the right child of the current node (root->right) to traverse the right subtree.
  * this recursive process repeats for each node in the binary tree, 
  * effectively performing an inorder traversal by visiting the nodes in the order of left subtree - current node - right subtree. 
  * each recursive call maintains its own set of variables and execution context, 
  * allowing the function to traverse the entire tree in an ordered manner.
  */ 
void inorder(struct treenode* root, int* res, int* ressize) {
    // check if the current node is null
    if (!root) {
        return;  // return if the current node is null
    }
    
    // traverse the left subtree in inorder
    inorder(root->left, res, ressize);
    
    // store the value of the current node in the result array and increment the size
    res[(*ressize)++] = root->val;
    
    // traverse the right subtree in inorder
    inorder(root->right, res, ressize);
    /*
     * `res[(*ressize)++] = root->val;`  is not needed here,
     * because the inorder traversal of a binary tree is structured in such a way that after traversing the left subtree and the current node, 
     * the traversal of the right subtree will naturally continue the process of storing the values in the correct order in the result array  `res` .
     * in an inorder traversal, the sequence of operations ensures that the left subtree is fully explored before visiting the current node, 
     * and then the right subtree is explored after the current node. 
     * therefore, by the time the function returns from the recursive call  `inorder(root->right, res, ressize);` , 
     * the right subtree has been traversed and the values have been stored in the result array in the correct order relative to the current node.
     * including  `res[(*ressize)++] = root->val;`  after the right subtree traversal would result in duplicating the value of the current node in the result array, 
     * which is unnecessary and would disrupt the correct inorder traversal sequence.
     */
}
/*
 * the  inordertraversal  function initializes the result array, 
 * calls the  inorder  function to perform the traversal, and then returns the result array. 
 */ 
int* inordertraversal(struct treenode* root, int* returnsize) {
    // allocate memory for the result array
    // create an integer array of size 501 dynamically on the heap and assigning the address of the first element of the array to the pointer variable  res .
    int* res = malloc(sizeof(int) * 501);
    
    // initialize the return size to 0
    *returnsize = 0;
    
    // perform inorder traversal starting from the root node
    inorder(root, res, returnsize);
    
    // return the result array containing the inorder traversal of the binary tree
    return res;
}

复杂度分析

时间复杂度：o(n)，其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。
空间复杂度：o(n)。空间复杂度取决于递归的栈深度，而栈深度在二叉树为一条链的情况下会达到 o(n)的级别。

方法二：迭代

思路与算法

方法一的递归函数我们也可以用迭代的方式实现，两种方式是等价的，区别在于递归的时候隐式地维护了一个栈，而我们在迭代的时候需要显式地将这个栈模拟出来，其他都相同。

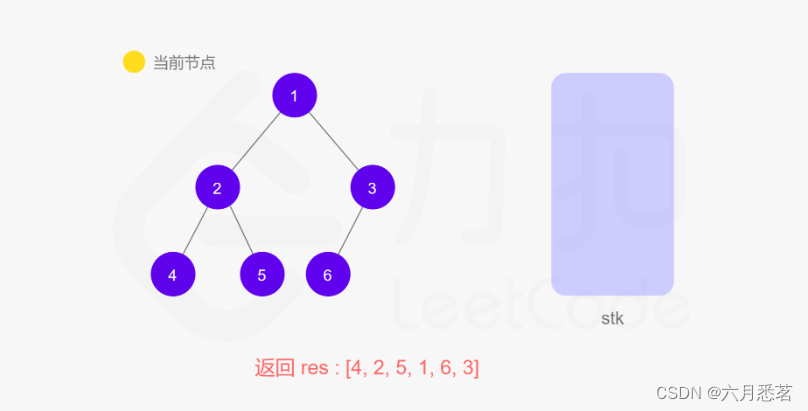
代码

/**
 * definition for a binary tree node.
 */
struct treenode {
    int val;
    struct treenode *left;
    struct treenode *right;
};
/**
 * an iterative version of the inorder traversal of a binary tree without using recursion.
 */
int* inordertraversal(struct treenode* root, int* returnsize) {
    // initialize return size to 0
    *returnsize = 0;
    
    // allocate memory for the result array
    int* res = malloc(sizeof(int) * 501);
    
    // allocate memory for the stack to keep track of nodes
    struct treenode** stk = malloc(sizeof(struct treenode*) * 501);
    
    // initialize top of the stack
    // variable top to keep track of the top of the stack. 
    int top = 0;
    
    // iterative inorder traversal using a stack
    // the while loop continues until the current node  root  is null and the stack is empty (indicated by  top > 0 ).
    while (root != null || top > 0) {
        // traverse left subtree and push nodes onto the stack 
        // a nested while loop to traverse the left subtree of the current node and pushes each node onto the stack. 
        while (root != null) {
            stk[top++] = root;
            root = root->left;
        }
        // check if the stack is not empty before popping
        if (top > 0)
        {
        	// once the left subtree is fully traversed
        	// pop a node from the stack
        	root = stk[--top];
        
        	// add the value of the popped node to the result array
        	res[(*returnsize)++] = root->val;
        
        	// move to the right child of the popped node
        	root = root->right;
        }
    }
    // free the memory allocated for the stack
    free(stk);
    
    // return the result array containing inorder traversal
    return res;
}

复杂度分析

时间复杂度：o(n)，其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。

空间复杂度：o(n)。空间复杂度取决于栈深度，而栈深度在二叉树为一条链的情况下会达到 o(n)的级别。

方法三：morris 中序遍历

思路与算法

morris 遍历算法是另一种遍历二叉树的方法，它能将非递归的中序遍历空间复杂度降为 o(1)。

morris 遍历算法整体步骤如下（假设当前遍历到的节点为 xxx）：

1. 如果 xxx 无左孩子，先将 xxx 的值加入答案数组，再访问 xxx 的右孩子，即 x=x.right。
2. 如果 xxx 有左孩子，则找到 xxx 左子树上最右的节点（即左子树中序遍历的最后一个节点，xxx 在中序遍历中的前驱节点），我们记为 predecessor。根据 predecessor 的右孩子是否为空，进行如下操作。
   • 如果 predecessor 的右孩子为空，则将其右孩子指向 xxx，然后访问 xxx 的左孩子，即 x=x.left。
   • 如果 predecessor\ 的右孩子不为空，则此时其右孩子指向 xxx，说明我们已经遍历完 xxx 的左子树，我们将 predecessor 的右孩子置空，将 xxx 的值加入答案数组，然后访问 xxx 的右孩子，即 x=x.right。
3. 重复上述操作，直至访问完整棵树。
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
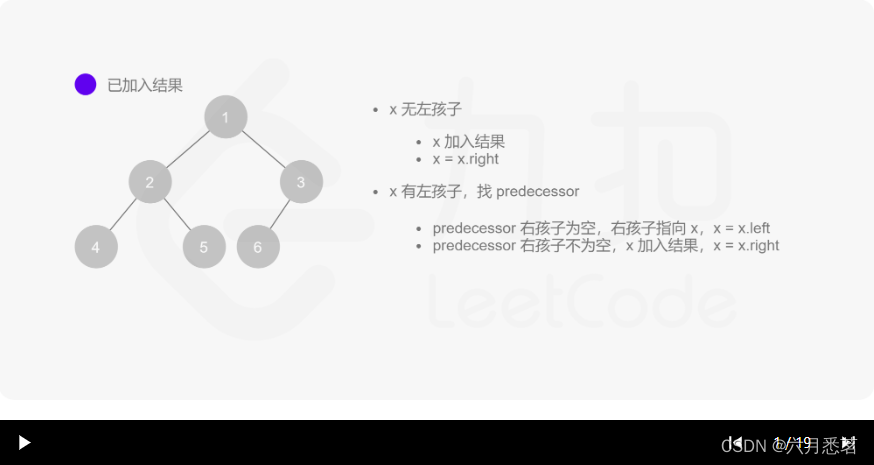
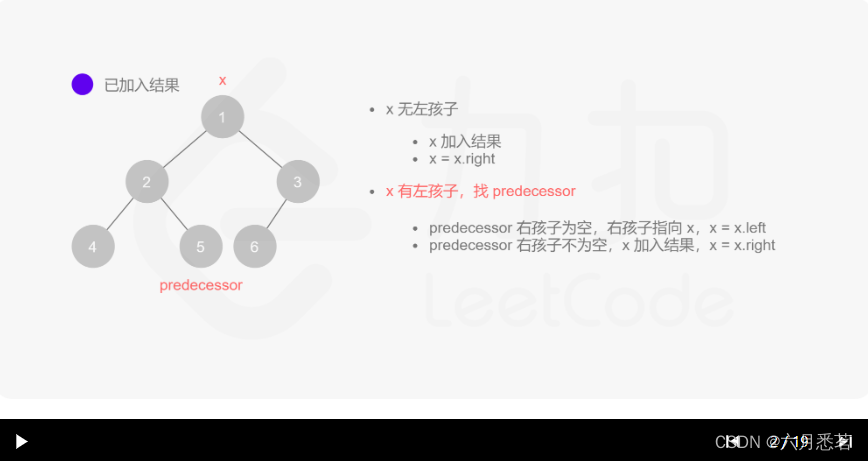
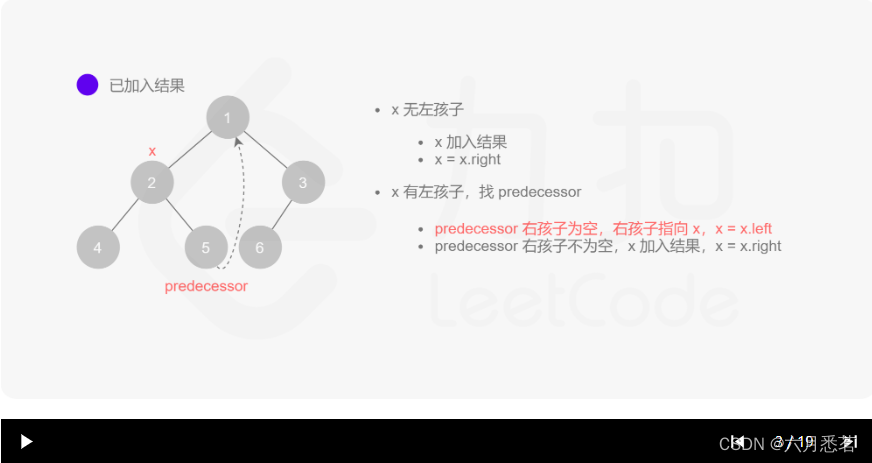
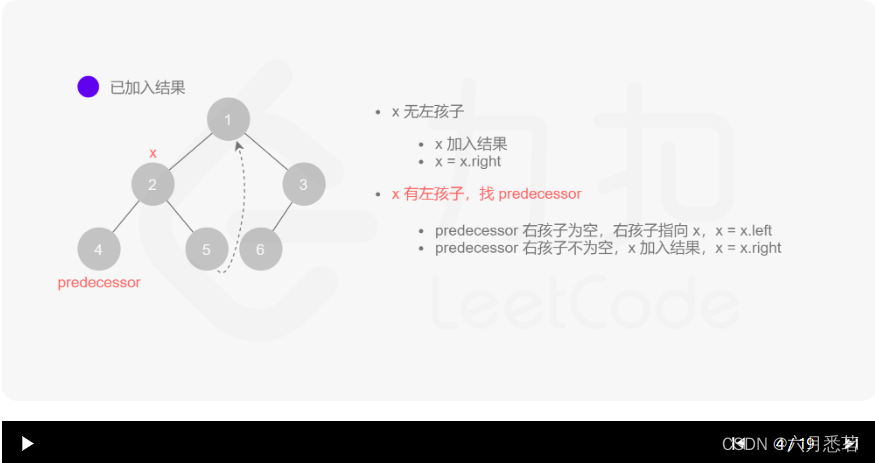
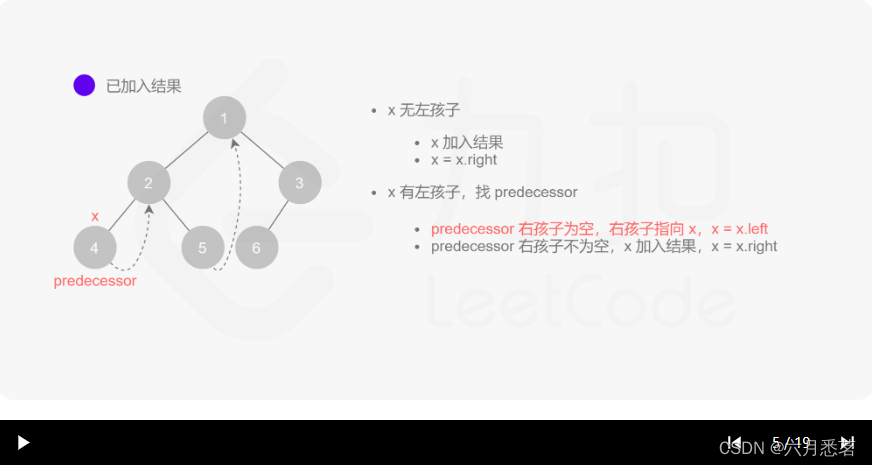
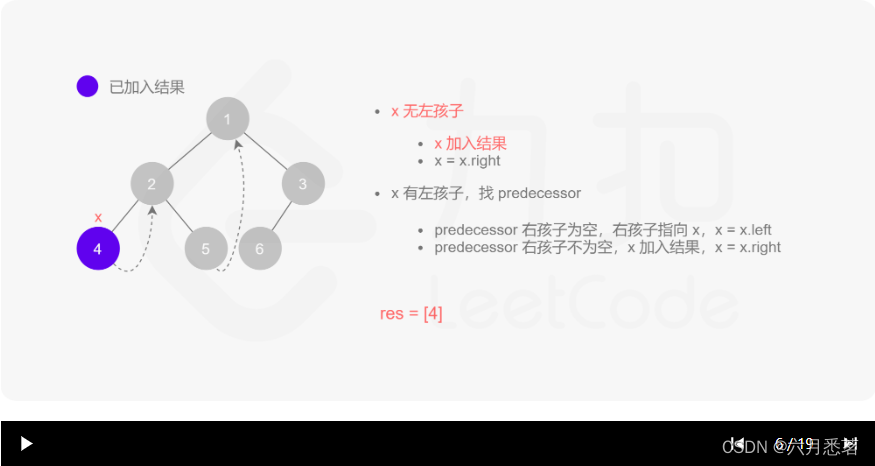
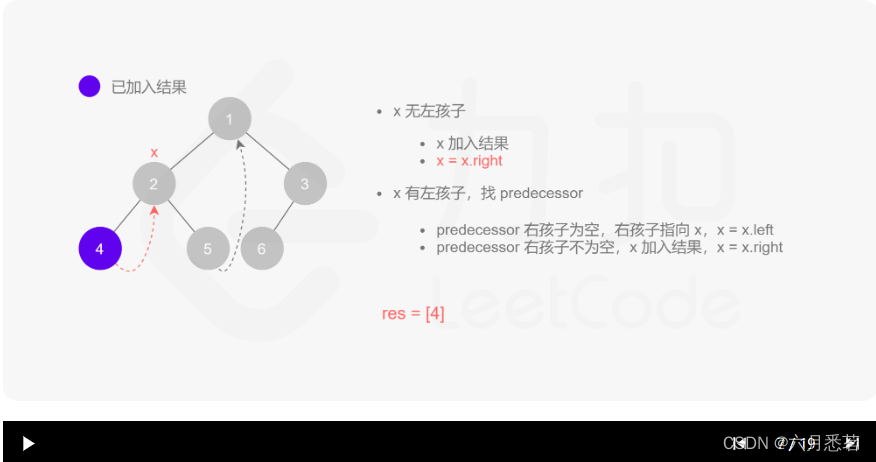
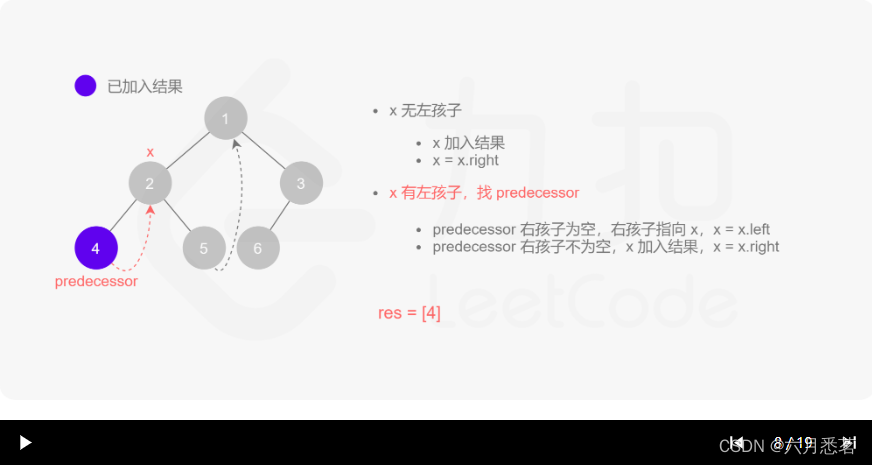
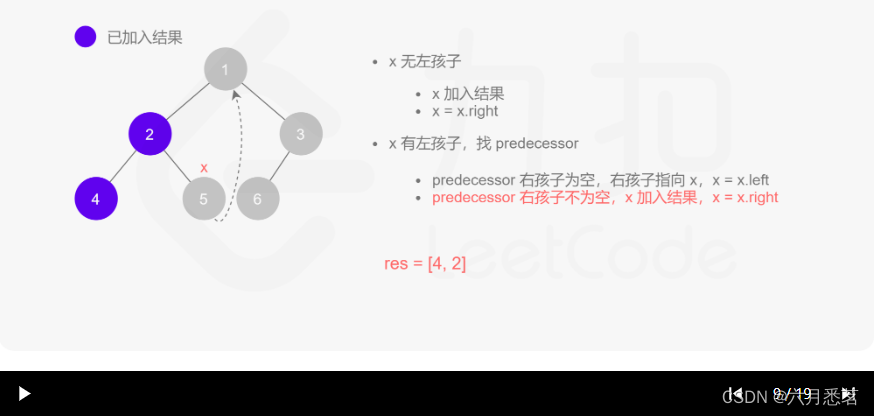
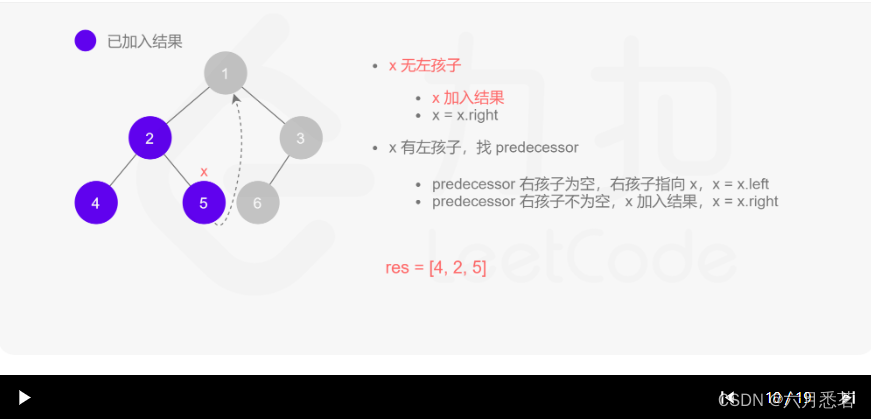
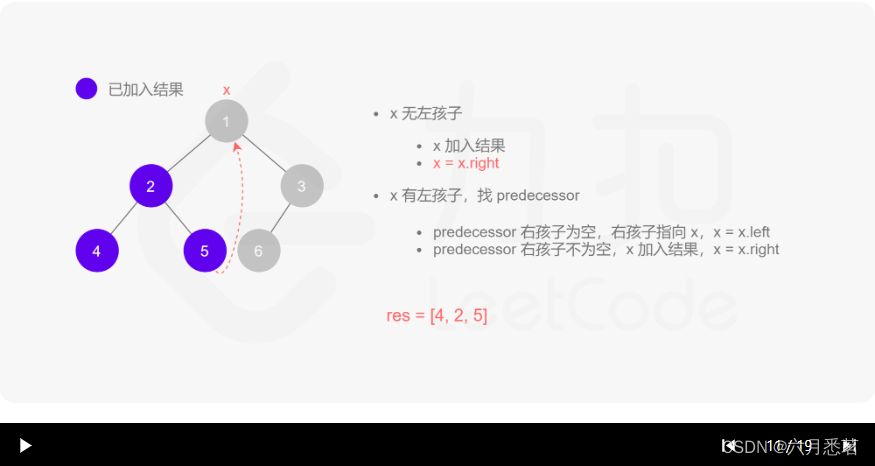
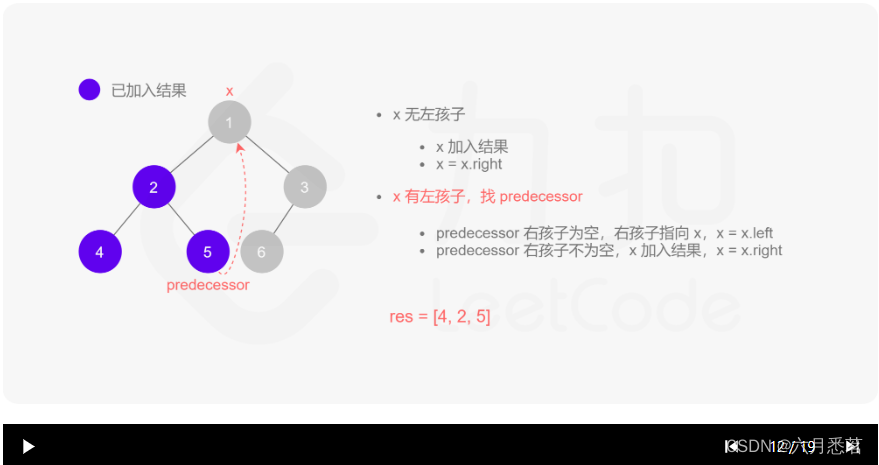
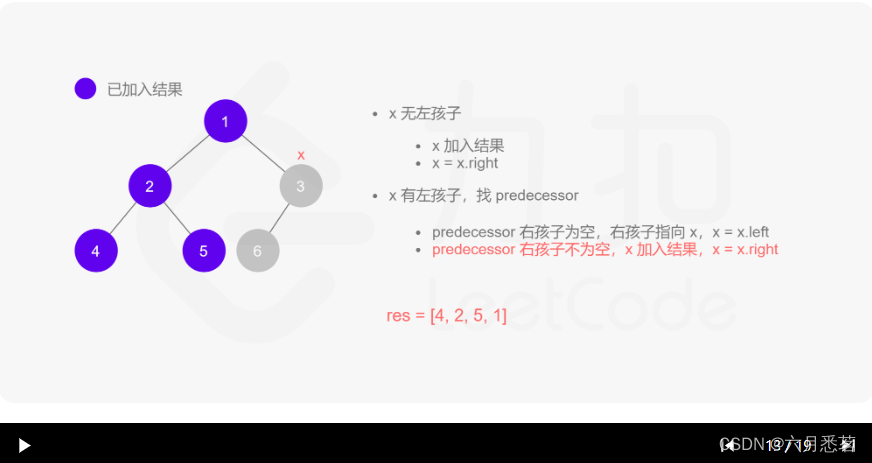
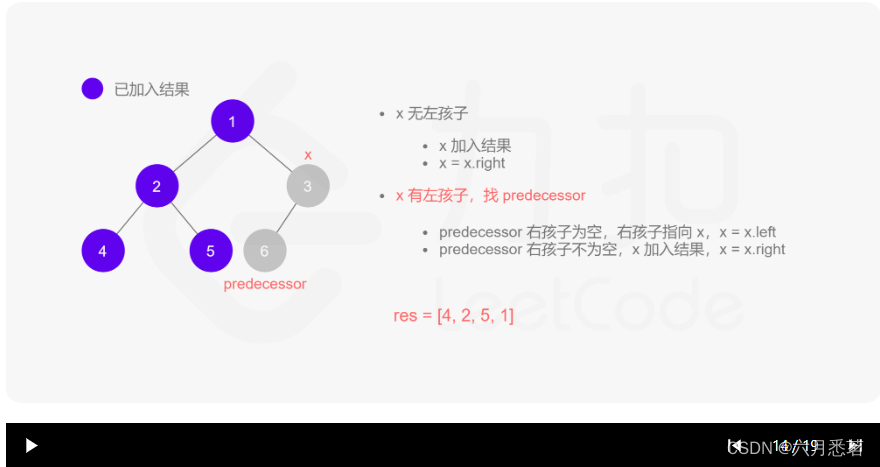
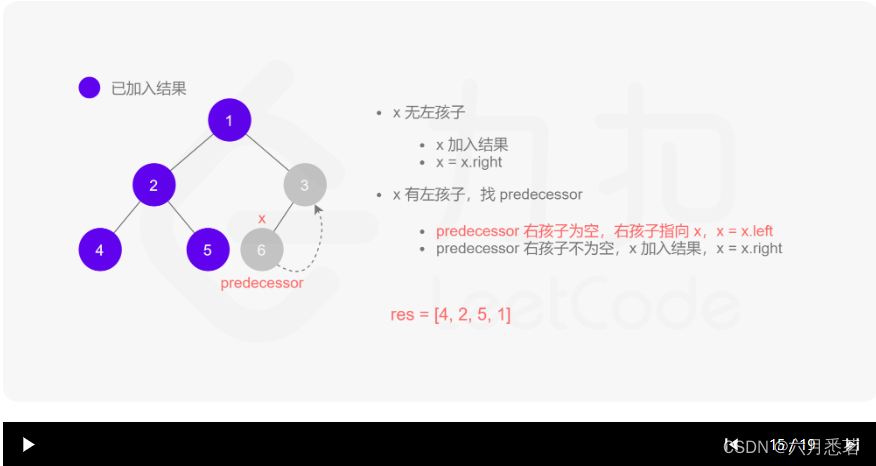
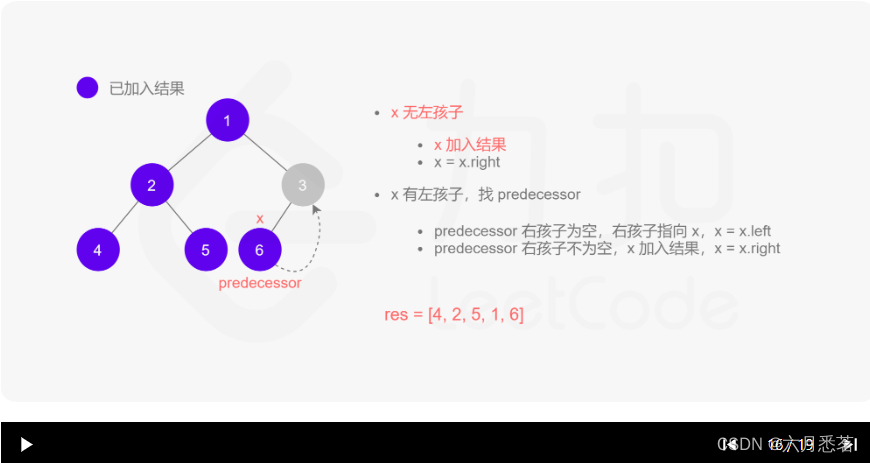
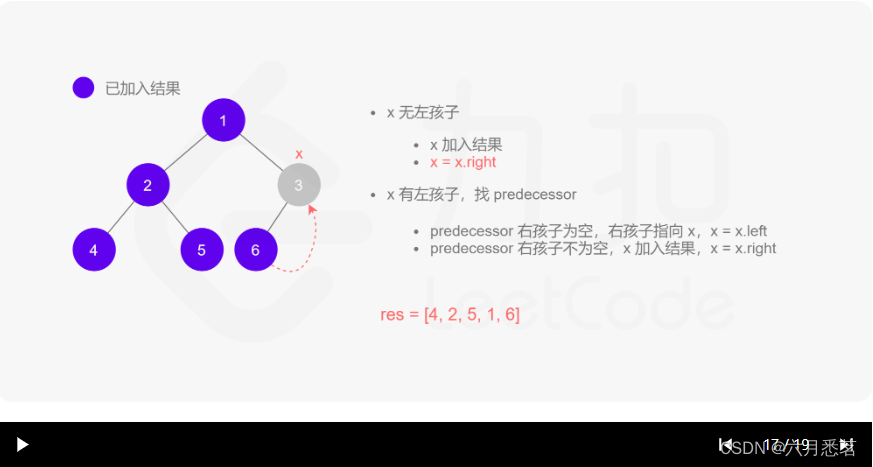
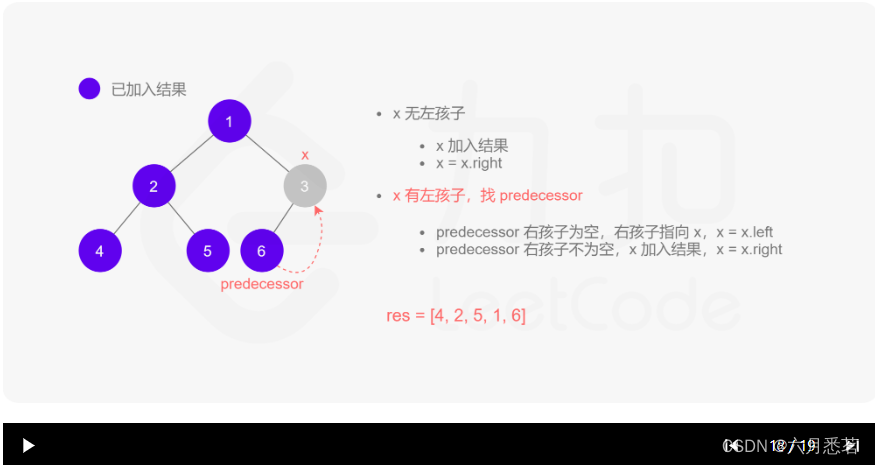
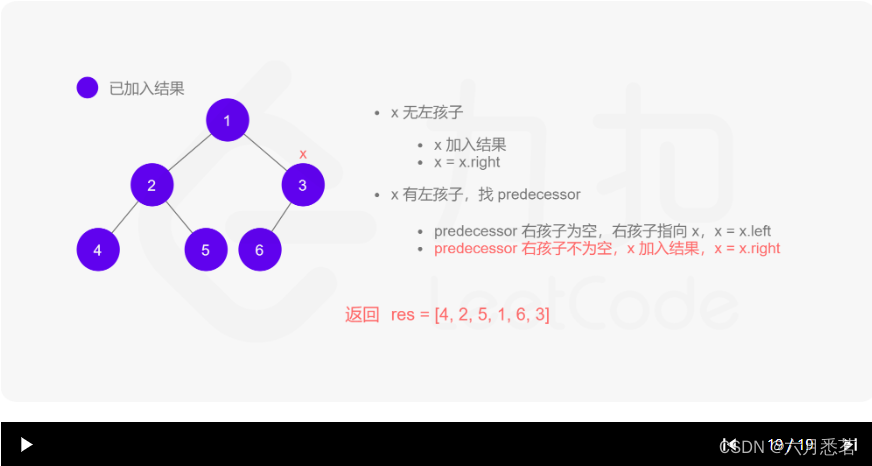
   其实整个过程我们就多做一步：假设当前遍历到的节点为 x，将 x 的左子树中最右边的节点的右孩子指向 x，这样在左子树遍历完成后我们通过这个指向走回了 x，且能通过这个指向知晓我们已经遍历完成了左子树，而不用再通过栈来维护，省去了栈的空间复杂度。

代码

/**
 * definition for a binary tree node.
 */
struct treenode {
    int val;
    struct treenode *left;
    struct treenode *right;
};
/**
 * the algorithm uses a predecessor node to establish temporary links 
 * between nodes to simulate the recursive call stack 
 * that would be used in a recursive inorder traversal. 
 * this approach allows for an iterative inorder traversal of the binary tree.
 */
int* inordertraversal(struct treenode* root, int* returnsize) {
    // allocate memory for the result array
    int* res = malloc(sizeof(int) * 501);
    
    // initialize return size to 0
    *returnsize = 0;
    
    // initialize predecessor node to null
    struct treenode* predecessor = null;
    
    // traverse the tree in inorder without using recursion
    while (root != null) {
        // if the current node has a left child
        if (root->left != null) {
            // find the predecessor node, which is the rightmost node in the left subtree
            predecessor = root->left;
            while (predecessor->right != null && predecessor->right != root) {
                predecessor = predecessor->right;
            }
            
            // if predecessor's right child is null, establish a link and move to the left child
            if (predecessor->right == null) {
                predecessor->right = root;
                root = root->left;
            }
            // if the left subtree has been visited, disconnect the link and move to the right child
            else {
                res[(*returnsize)++] = root->val;
                predecessor->right = null;
                root = root->right;
            }
        }
        // if there is no left child, visit the current node and move to the right child
        else {
            res[(*returnsize)++] = root->val;
            root = root->right;
        }
    }
    
    // return the result array containing inorder traversal
    return res;
}

复杂度分析

时间复杂度：o(n)，其中 n 为二叉树的节点个数。morris 遍历中每个节点会被访问两次，因此总时间复杂度为 o(2n)=o(n)。

空间复杂度：o(1)。

作者：力扣官方题解
链接：https://leetcode.cn/problems/binary-tree-inorder-traversal/solutions/412886/er-cha-shu-de-zhong-xu-bian-li-by-leetcode-solutio/
来源：力扣（leetcode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。