决策树
有删改。
先了解一个概念,熵(entropy):是衡量数据集不确定性的指标,其计算公式为:

1、基于信息增益-- id3
信息增益衡量的是基于一个特征进行分割后,数据集熵的减少量。

通俗解释:根节点的熵减去特征分割后的熵,分割后的熵等于特征各类别熵的加权和。
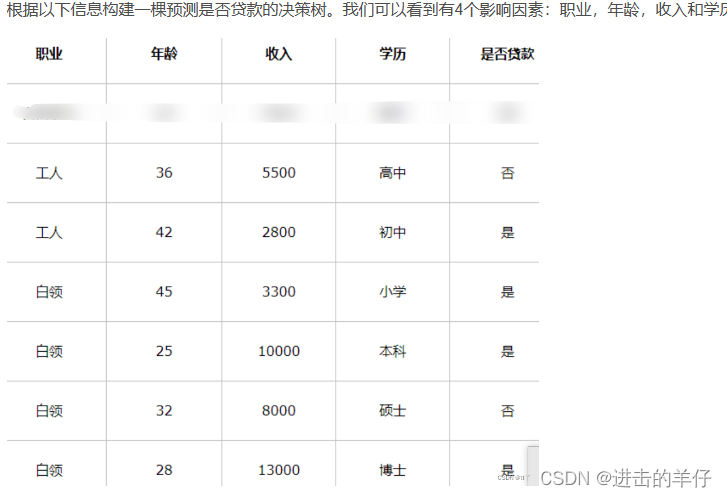
1、计算根节点的信息熵
共有6个样本,根节点“是否贷款”中,4个“是”,占2/3;2个“否”,占1/3。

2、计算特征的信息增益
例:“职业”特征中,“工人”占总体样本的1/3;所有“工人”里面“是否贷款”为“是”的占所有工人的1/2,那么"工人"类别的熵就等于
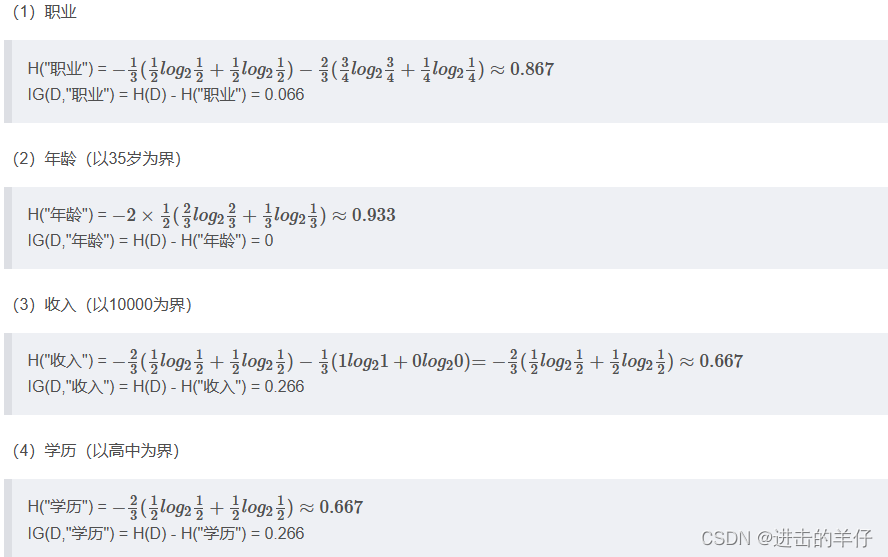
选择信息增益最大的属性作为划分属性
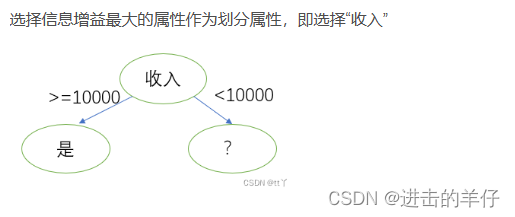
3、接下来继续重复1,2的做法继续寻找合适的属性节点

注:信息增益准则对可取值数目较多的属性有所偏好(偏向于选择取值较多的特征),为减少这种偏好可能带来的不利影响,有些决策树算法不以信息增益作为最优划分属性的选择依据,而选择增益率。
2、基于增益率--c4.5
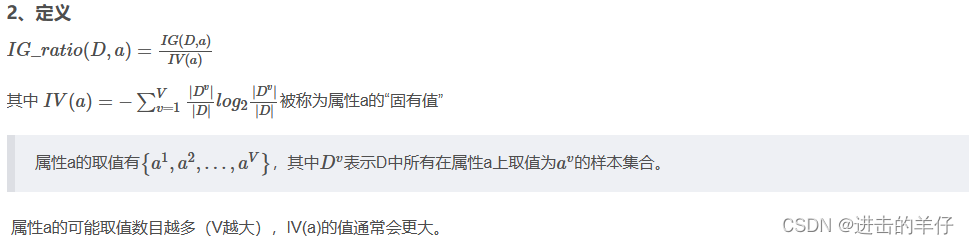

4、注意点
增益率准则对可取值数目较少的属性有所偏好。
因此基于增益率的决策树建立方法:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的(而非直接用增益率作为比对标准)。
3、基于基尼指数--cart决策树
1、定义
(1)基尼值
![]()
gini(d)反映了从数据集d中随机抽取两个样本,其类别标记不一致的概率,表示数据集整体的不确定性。
gini(d)越小,数据集d的纯度越高,不确定性越小。
(2)基尼指数
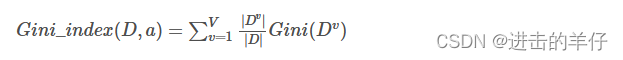
表示经a分割后数据集d的不确定性。
(3)基尼不纯度的减少量
计算公式为:
![]()
2、决策树建立方法(分类回归均可用)
分类:在侯选属性集合中,选择那个是的划分后基尼指数最小的属性为最优划分属性。
回归:用平方误差最小化准则
4、剪枝
1、提出原因
决策树分支可能过多,以致于把训练集自身的一些特征当作所有数据都具有的一般性质而导致过拟合。决策树越复杂,过拟合的程度会越高。因此我们主动去掉一些分支来降低过拟合的风险。
2、剪枝与其处理基本策略
(1)剪枝:剪枝是指将一颗子树的子节点全部删掉,根节点作为叶子节点。
(2)基本策略:预剪枝和后剪枝
3、预剪枝
(1)做法
在决策树生成的过程中,每个决策节点原本是按照信息增益、信息增益率或者基尼指数等纯度指标,按照值越大,优先级越高来排布节点。由于预剪枝操作,所以对每个节点在划分之前要对节点进行是否剪枝判断,即:使用验证集按照该节点的划分规则得出结果。若验证集精度提升,则不进行裁剪,划分得以确定;若验证集精度不变或者下降,则进行裁剪,并将当前节点标记为叶子节点。
(2)具体例子
比如上述例子中的“学历”
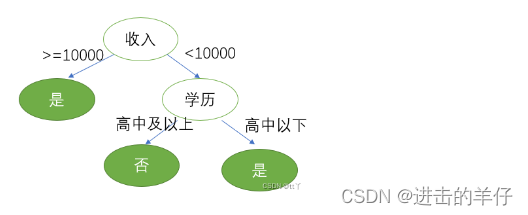
我们选取第5个样本为验证集
若不划分:验证集精度为50%(一半是,一半否);若划分:验证集精度100%。
所以需要划分,不剪枝。
(3)优缺点
🎈优点:预剪枝使得决策树很多相关性不大的分支都没有展开,这不仅仅降低了过拟合的风险,还显著减少了决策树的训练时间开销和测试时间开销。
🎈缺点:有些分支的当前划分虽不能提升泛化能力,甚至可能导致泛化能力暂时下降,但是在其基础上进行的后续划分却有可能提高性能。预剪枝基于“贪心”本质禁止这些分支展开,给预剪枝决策树带来了欠拟合的风险。
4、后剪枝
(1)做法
已经通过训练集生成一颗决策树,然后自底向上地对决策节点(非叶子结点)用测试集进行考察,若将该节点对应的子树替换为叶子节点能提升验证集的精确度(这个的算法与预剪枝类似),则将该子树替换成叶子节点,该决策树泛化能力提升。
(2)优缺点
🎈优点:后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般情况下,后剪枝决策树的欠拟合风险很小,泛化能力往往优于预剪枝决策树。
🎈缺点:后剪枝过程是在生成完决策树之后进行的,并且要自底向上地对树中的所有决策节点进行逐一考察,因此其训练时间开销比未剪枝的决策树和预剪枝决策树都要大得多。
5、另外一种剪枝方法——在生成决策树后通过极小化决策树整体的损失函数来实现
![]()


原文转载:

发表评论