目录
三、逻辑回归(logistic regression)与神经网络
具体应用:预测客户是否有意预订有线电视交互服务
一、背景介绍
当今时代,有线电视交互服务已经成为人们日常生活中的一个重要组成部分。这种服务能够提供多样化的娱乐和信息,吸引了越来越多的消费者。然而,对于电视运营商来说,如何判断客户是否有意向预订这种服务是一个非常重要的问题。如果可以在客户购买前就预测出客户是否有购买该服务的意向,那么电视运营商就能够制定相应的销售策略来提高销售额。因此,通过机器学习算法来预测客户是否有意购买有线电视交互服务是一个非常有实际应用价值的任务。而逻辑回归和神经网络是常用的分类算法,可以用于这个任务。在本文中,我们将介绍如何使用逻辑回归和神经网络来预测客户是否有意购买有线电视交互服务,并分析模型的准确性和性能。
二、题目要求
业务:预测客户是否有意预订有线电视交互服务;
输入变量:年龄、性别、教育、收入类别、每天看电视的时间和子女数
输出变量:newschan
算法:逻辑回归和神经网络
效果评估:gains
三、逻辑回归(logistic regression)与神经网络
逻辑回归是一种广泛应用于二分类问题的线性模型。它基于输入特征的线性组合,通过一个sigmoid函数将输出映射到0和1之间的概率值。逻辑回归可以用于预测某个样本属于某个类别的概率。逻辑回归也称作logistic回归分析,是一种广义的线性回归分析模型,属于机器学习中的监督学习。其推导过程与计算方式类似于回归的过程,但实际上主要是用来解决二分类问题(也可以解决多分类问题)。通过给定的n组数据(训练集)来训练模型,并在训练结束后对给定的一组或多组数据(测试集)进行分类。其中每一组数据都是由p 个指标构成。
神经网络(也称为人工神经网络)是一种模仿人脑神经元之间连接的数学模型。它由输入层、隐藏层(可能有多层)和输出层组成。每个神经元都接收来自上一层神经元的输入,经过权重和激活函数的处理后,将输出传递给下一层神经元。神经网络通过学习调整权重来逼近训练数据的输出。
相比逻辑回归,神经网络在处理非线性问题时更加强大。神经网络可以通过调整隐藏层的神经元数量和层级,以及选择不同的激活函数和损失函数,来适应各种复杂的数据模式。它在计算机视觉、自然语言处理和推荐系统等领域取得了很大成功。
四、输入输出变量
在预测客户是否有意预订有线电视交互服务的问题中,有多个输入变量可以用于构建逻辑回归或神经网络模型。以下是一些常用的输入变量:
通过这些输入变量,逻辑回归或神经网络模型可以尝试预测客户是否有意预订有线电视交互服务,帮助有线电视运营商更好地了解客户需求,制定更好的销售策略和服务。
在预测客户是否有意预订有线电视交互服务的问题中,一个重要的输出变量是newschan,即新闻频道。 它是指客户是否订阅了有线电视运营商提供的新闻频道服务。 新闻频道是有线电视服务的一个重要组成部分,提供丰富的新闻资讯和专题节目,受到了广大观众的喜爱。newschan这个输出变量是一个二元变量,1表示订阅了新闻频道服务,0表示没有订阅。它是一个关键的预测变量,因为与有线电视交互服务相关的特征很可能与订阅新闻频道服务有关。比如说,一个客户订阅了新闻频道服务,很可能表明他们对新闻和信息的需求比较高,同时也可能意味着他们对其他有线电视服务的需求也比较高。输出变量newschan的预测结果,将为电视运营商的公司发展和销售策略做出决策提供有价值的信息。 如果通过逻辑回归或神经网络等分类算法能够成功的预测出客户是否订阅了新闻频道服务,将可以为电视公司提供重要的数据支持,以便公司能够更好地为客户定制服务。
五、效果评估gains介绍
在机器学习中,对模型性能进行评估非常重要,选择适当的评估指标是保证模型成功的关键之一。gains是一种常用的评估模型性能的方式,它可以衡量分类算法在预测结果时的效果,并与随机方法进行比较。
gains原理的核心是,将样本按照预测结果的概率值从高到低进行排序,然后计算分类算法在不同预测概率值下的累积收益率曲线。累积收益率曲线(cumulative gain curve)展示了针对某个标注为1的类别问题的(比如说欺诈检测)在不同置信区间内预测的准确率。通常情况下,我们需要确认两个基准线。第一个基准线指的是总人口比例下标注为1的比例,第二个基准线是在保持总人口比例的同时,标注为1的人数/max(1,标注为1的总人数)。将累积收益率曲线与随机曲线进行比较可以评估模型的准确性和性能。随机曲线表示的是随机预测的结果,它帮助我们评估模型准确率的下限。如果模型的累积收益率曲线高于随机曲线,就说明分类器的性能比随机猜测要好。
gains方法的优点是简单易用,并且可以用来比较不同算法的表现。它也有缺点,比如它不能检测出分类过程中的错误,而只能衡量预测的准确度。因此,在使用gains方法时需要注意解释结果的含义以及它的有限性。
六、模型构建
代码:
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import logisticregression
from sklearn.neural_network import mlpclassifier
from sklearn.impute import simpleimputer
from sklearn.metrics import classification_report, roc_curve, auc
import matplotlib.pyplot as plt
# 读取excel数据
data_path = r'e:\研究生学习\人工智能训练营\第三次作业\tvdata.xlsx'
df = pd.read_excel(data_path)
# 提取输入变量和输出变量
x = df[['educate', 'gender', 'age', 'tvday', 'orgs', 'childs', 'inc']]
y = df['newschan']
# 使用simpleimputer将缺失值填充为0
imputer = simpleimputer(strategy='constant', fill_value=0)
x = imputer.fit_transform(x)
# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)
# 构建逻辑回归模型
logreg = logisticregression()
logreg.fit(x_train, y_train)
# 在测试集上进行预测
logreg_pred = logreg.predict(x_test)
# 输出分类报告
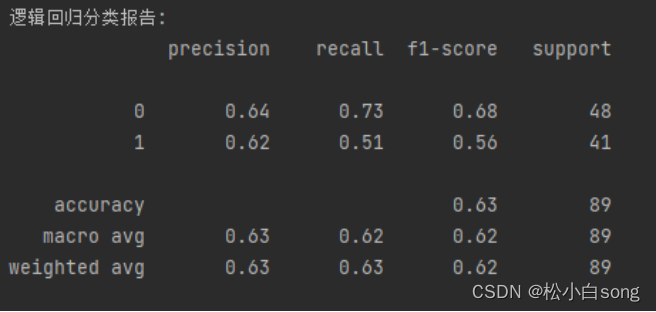
print("逻辑回归分类报告:")
print(classification_report(y_test, logreg_pred))
# 计算roc曲线的参数
y_scores = logreg.predict_proba(x_test)[:, 1]
fpr, tpr, thresholds = roc_curve(y_test, y_scores)
roc_auc = auc(fpr, tpr)
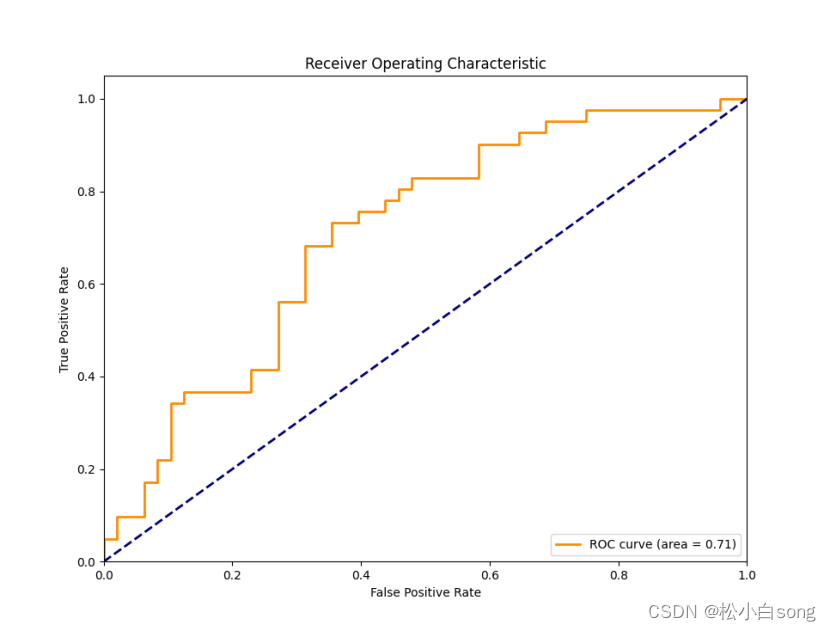
# 绘制roc曲线
plt.plot(fpr, tpr, color='darkorange', lw=2, label='roc curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('false positive rate')
plt.ylabel('true positive rate')
plt.title('receiver operating characteristic')
plt.legend(loc="lower right")
plt.show()结果:



发表评论