lasso回归/岭回归的原理
在学习l1,l2正则化的作用和区别时,我们总是会看到这样的一副图片:
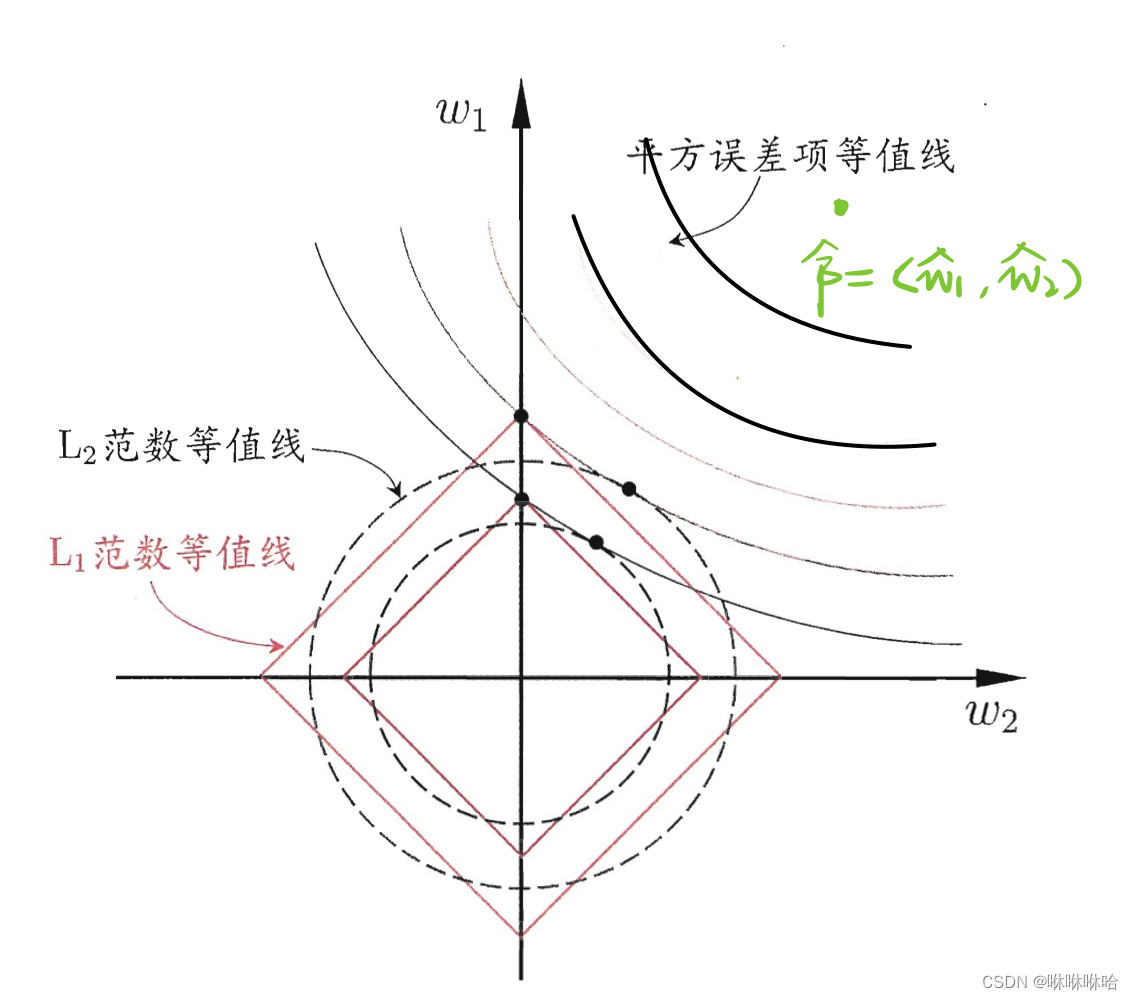
这幅图片形象化地解释了l1,l2对线性模型产生的不同的约束效果。
我最开始其实是不太理解为什么要这么画的。比如
1、l1范数(l1-norm)等值线一定会和平方误差项等值线相交于某一坐标轴吗?
2、lasso回归只能用平方和误差作为损失吗,换成交叉熵可以吗?
3、除了l1-norm,l2-norm,还有没有别的正则化方法,他们的区别是什么?
见我的另一篇博客lasso回归系列三:机器学习中的l0, l1, l2, l2,1范数
现在算是搞明白了,结合网上很不错的几篇博客,再梳理一下,分享给大家,如有不足或者错误,请多多指正。
概述
使用l1正则化项的回归模型被称作lasso回归(lasso regression),使用l2正则化项的回归模型被称作岭回归(ridge regression)。
所以只要是回归问题中加入l1正则项,都可以称为lasso回归,并非只限于使用平方和误差作损失的情况。
在本文中,首先,我们会了解在使用最小二乘估求解线性回归问题时,加入l1-norm的lasso回归,加入l2-norm的岭回归会使求解发生哪些变化,从而更好地理解如何使用lasso回归和岭回归。
线性模型的最小二乘估
在对线性模型进行参数估计时,可以使用最小二乘法。
用数学语言来描述,线性模型可以表示为:
y
=
x
β
+
ϵ
e
(
ϵ
)
=
0
,
c
o
v
(
ϵ
)
=
σ
2
i
y = x\beta +\epsilon \\e(\epsilon)=0, cov(\epsilon) = \sigma^2 i
y=xβ+ϵe(ϵ)=0,cov(ϵ)=σ2i
其中
y
y
y 是
n
×
1
n \times 1
n×1的标签向量,
x
x
x 是
n
×
p
n \times p
n×p的特征矩阵(对应到数据上,
n
n
n是样本数,
p
p
p是特征数量) ,
β
\beta
β ,
ϵ
\epsilon
ϵ是要估计的参数,
β
\beta
β 是
p
×
1
p \times 1
p×1的未知参数向量,
ϵ
\epsilon
ϵ 是随机误差。
最小二乘法是估计参数向量
β
\beta
β 的基本方法,其思想是让误差尽可能得小,也即$\epsilon = y- x\beta $ 尽可能得小,也即是使
q
(
β
)
=
∣
∣
ϵ
∣
∣
2
=
∣
∣
y
−
x
β
∣
∣
2
=
(
y
−
x
β
)
t
(
y
−
x
β
)
q(\beta) = ||\epsilon||^2 = ||y-x\beta||^2 = (y-x\beta)^t(y-x\beta)
q(β)=∣∣ϵ∣∣2=∣∣y−xβ∣∣2=(y−xβ)t(y−xβ)
尽可能得小。
根据凸函数极小值就是最小值的定理,我们可以通过求得偏导等于0处的
β
\beta
β 值,使得上式达到最小值,即:
β
^
=
(
x
t
x
)
−
1
x
t
y
\hat\beta = (x^tx)^{-1}x^ty
β^=(xtx)−1xty
结合矩阵论中的知识,当
r
a
n
k
(
x
)
=
p
rank(x)=p
rank(x)=p 时,
x
t
x
x^tx
xtx 可逆,这时
β
\beta
β 有唯一解,$\hat\beta = \beta $,称 $ \hat\beta $ 是 $ \beta $ 的无偏估计;当
r
a
n
k
(
x
)
<
p
rank(x)<p
rank(x)<p 时,
x
x
x 矩阵不满秩,此时我们无法得到$ \beta $ 的无偏估计,而导致
r
a
n
k
(
x
)
<
p
rank(x)<p
rank(x)<p 的原因一般有两种:1、样本数小于特征数量,2、即使样本数较多,但变量(特征)之间存在线性关系,lasso回归和ridge(岭回归)就是用来解决这一问题的。
lasso回归和ridge回归
lasso回归(lasso regression)是在目标函数后加一个权重
β
\beta
β 的1-范数(机器学习中的范数定义不同于数学中的定义,具体定义请看【https://xiongyiming.blog.csdn.net/article/details/81673491】),即:
q
(
β
)
=
∣
∣
y
−
x
β
∣
∣
2
2
+
λ
∣
∣
β
∣
∣
1
⟺
arg
min
∣
∣
y
−
x
β
∣
∣
2
s
.
t
.
∑
∣
β
j
∣
≤
s
q(\beta) = ||y-x\beta||^2_2 + \lambda ||\beta||_1 \\ \quad \iff \\ \arg \min ||y-x\beta||^2 \quad s.t. \sum |\beta_j| \leq s
q(β)=∣∣y−xβ∣∣22+λ∣∣β∣∣1⟺argmin∣∣y−xβ∣∣2s.t.∑∣βj∣≤s
岭回归(ridge regression)是在目标函数后加一个权重
β
\beta
β 的2-范数,即:
q
(
β
)
=
∣
∣
y
−
x
β
∣
∣
2
2
+
λ
∣
∣
β
∣
∣
2
⟺
arg
min
∣
∣
y
−
x
β
∣
∣
2
s
.
t
.
∑
β
j
2
≤
s
q(\beta) = ||y-x\beta||^2_2 + \lambda ||\beta||_2 \\ \quad \iff \\ \arg \min ||y-x\beta||^2 \quad s.t. \sum \beta_j^2 \leq s
q(β)=∣∣y−xβ∣∣22+λ∣∣β∣∣2⟺argmin∣∣y−xβ∣∣2s.t.∑βj2≤s
对上式求解,可以得到
β
\beta
β 的岭估计:
β
^
(
λ
)
=
(
x
t
x
+
λ
i
)
−
1
x
t
y
\hat\beta(\lambda) = (x^tx+\lambda i)^{-1}x^ty
β^(λ)=(xtx+λi)−1xty
这样确保
x
t
x
+
λ
i
x^tx+\lambda i
xtx+λi 满秩,可逆,当然此时的
β
^
(
λ
)
\hat\beta(\lambda)
β^(λ) 是一个有偏估计。
lasso回归为什么更容易产生稀疏解?
我们再看下这幅图:

平方误差等值线即 q ( β ) = ∣ ∣ y − x β ∣ ∣ 2 q(\beta) = ||y-x\beta||^2 q(β)=∣∣y−xβ∣∣2 对应的等势线
lasso回归对应l1范数等值线,ridge回归对应l2范数等值线,两者均通过正则项参数 λ \lambda λ 来调节对参数 β \beta β 的约束程度。
lasso回归容易产生稀疏解,是因为l1范数包含了一些在坐标轴上的不可微的角点(non-differentiable corner ),这些角点和 q ( β ) = ∣ ∣ y − x β ∣ ∣ 2 q(\beta) = ||y-x\beta||^2 q(β)=∣∣y−xβ∣∣2 相交的概率会大很多。而在ridge回归中,l2范数是处处可微的,所以和 q ( β ) = ∣ ∣ y − x β ∣ ∣ 2 q(\beta) = ||y-x\beta||^2 q(β)=∣∣y−xβ∣∣2在坐标轴上相交的概率会小很多。
此外,对于l1范数来说, λ \lambda λ 越大, ∣ ∣ β ∣ ∣ 1 ||\beta||_1 ∣∣β∣∣1 的范围越小,平方误差等值线和l1范数等值线在坐标轴上相交的概率就越大,也就是说 β \beta β 中的元素变成0的概率越大。反之, β \beta β 中的元素变成0的概率则越小。
参考



发表评论