

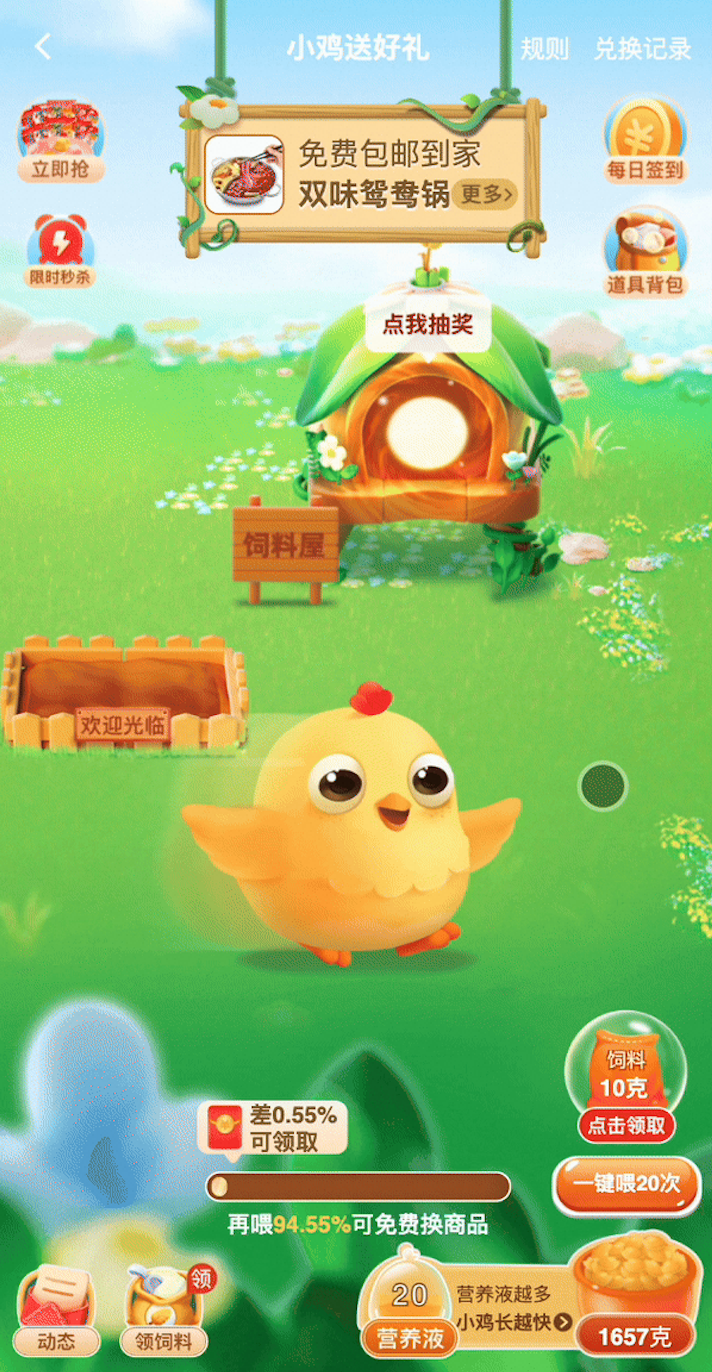
近期pd找到我,说我们的特价版小鸡送好礼要进行大改版,要让小鸡在地图上自由的走动起来,期间会遇到各种随机事件、玩法,从而提高趣味性和业务指标。交互图如下:

-
小鸡如何行走,是否需要前、后、左、右、左上、左下、右上、右下八个动画; -
遇到建筑物、河流如何处理; -
交互稿子上有景深的效果、有道路,小鸡如何做到在道路上走、和远景房子等融合。

行走
和设计一起看了一些人物扮演游戏,自己也想了一下dnf、三国这些2d游戏,没我们想得那么复杂需要八个方向不同的动画,不区分奔跑的话就两种动画,左下和右下就能满足大部分场景。
设计师:
|
|
|
|
|
|

▐ 方案一:基于射线投射的寻路算法
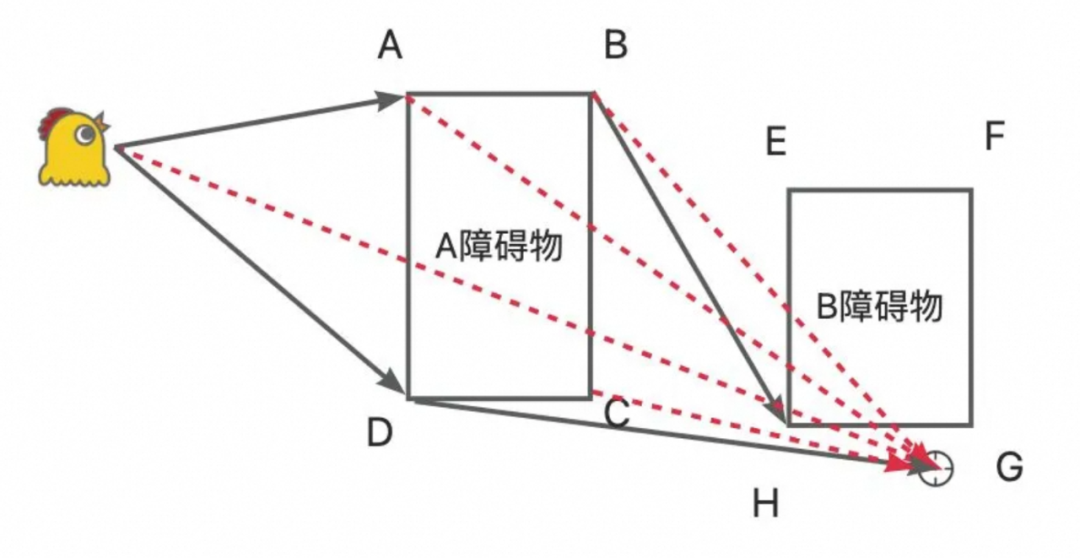
这是我一开始想到的思路,但存在不少问题。
具体的路径计算步骤为:
-
从起点发射一条射线到目标点。 -
如果射线直达目标点而不与任何障碍物相交,那么路径就是直线,寻路结束。 -
如果射线与障碍物交叉了,确定射线与哪个障碍物边界相交,并且找到这个边界的两个顶点。 -
对每一个顶点,计算从起点到顶点的直线距离。 -
将每个顶点视为新的起点,从这些顶点发射新的射线到目标点。 -
重复步骤2至5,直至找到不被障碍物阻断的直线路径,或者确定所有可能路径都检查完毕。 -
计算所有可能路径的长度,并选取最短路径。
图上所示全路径:
a-b-e-f-g-目标点
a-b-e-h-目标点
a-b-h-目标点
a-b-c-目标点
a-d-目标点(最优解)
-
a-d-c-目标点
该方案存在的问题:
-
计算成本高,需要大量射线投射和碰撞检测计算,每次遇到障碍物都需要寻找交叉点并再次发射新的射线。在大型地图或高度动态的环境中,这可能会导致性能问题; -
路径并非最优,算法可能找到一个避开障碍物的路径,但不一定是最短或最高效的路径。根据障碍物的布局和顶点的选择,最终的路径可能远远绕过障碍物,而不是采取更合理或直接的路线; 不适合所有类型环境,试用于简单的矩形障碍物场景,遇到复杂的障碍物图形,如迷宫、凹凸类型的多边形,可能难以找到一个有效的通路。
▐ 方案二:基于a*的寻路算法
a*算法是一种栅格化地图上常用的高效寻路算法,利用估算的成本函数来遍历节点,从而找到一条从起点到终点的最短路径,这也是大部分游戏在使用的路径计算方法。
采用某乎上的一些分析例子和思路,a*搜索算法(a-star search)简介。
介绍一下概念,每个栅格即为一个node节点,每个节点都有自己的三个属性值
-
g为从起点走到当前格子的成本; -
h为当前格子到终点的估计成本,使用的曼哈顿距离,即为 |x1 - x2| + |y1 - y2|; -
f为g值和h值的总和; -
openlist为待计算的点; -
closelist为已选中的点
以一个简单的3*3的栅格介绍一下整体的a*算法的流程,初始点为(0, 0),目标点为(2, 2),格子的长宽皆为1、斜角的长度为1.4。
7. 循环4-6步,直到h为0时,即找到最短路径。
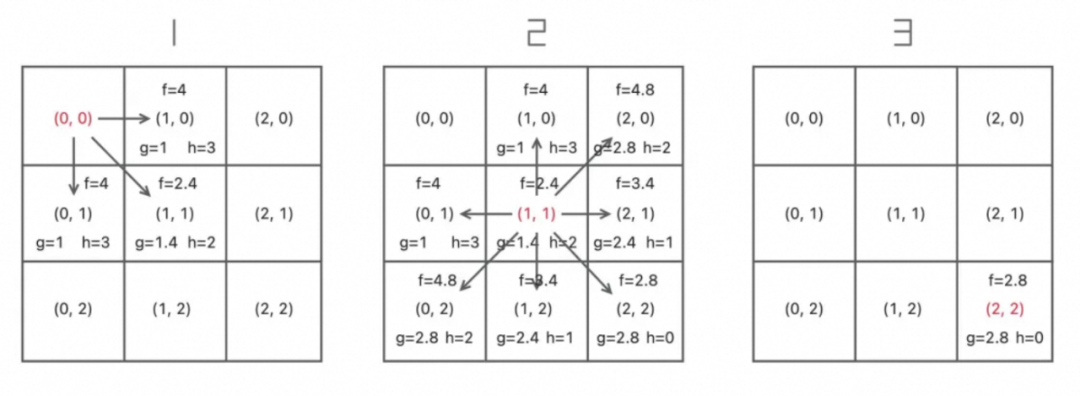
写了一个简单的以javascript实现的版本:
// a*算法 node 类,用于存储节点信息class node {constructor(parent = null, position = null) {this.parent = parent; // 父节点this.position = position; // 节点在网格中的坐标位置this.g = 0; // g值是从起点走到当前格子的成本this.h = 0; // h值是当前格子到终点的估计成本this.f = 0; // f值是g值和h值的总和}// 判断两个节点是否位于同一个位置isequal(othernode) {return this.position[0] === othernode.position[0] && this.position[1] === othernode.position[1];}}// 启发式函数,用于估计到达目标的成本(此处使用曼哈顿距离)function heuristic(nodea, nodeb) {const d1 = math.abs(nodeb.position[0] - nodea.position[0]);const d2 = math.abs(nodeb.position[1] - nodea.position[1]);return d1 + d2;}// 获取一个节点的所有可能的邻居(包括对角线上的位置)function getneighbors(currentnode, grid) {const neighbors = [];// 这里包括了八个方向上的移动const directions = [[-1, -1], [-1, 0], [-1, 1], // 左上 左 左下[0, -1], [0, 1], // 上 下[1, -1], [1, 0], [1, 1], // 右上 右 右下];// 查看每个方向的邻居是否可通行(非障碍)且在网格范围内for (const direction of directions) {const neighborpos = [currentnode.position[0] + direction[0],currentnode.position[1] + direction[1],];// 确保位置在网格内且不是障碍物if (neighborpos[0] >= 0 && neighborpos[0] < grid.length &&neighborpos[1] >= 0 && neighborpos[1] < grid[0].length &&grid[neighborpos[0]][neighborpos[1]] === 1) {neighbors.push(new node(currentnode, neighborpos));}}return neighbors;}// a* 算法主函数function astar(grid, start, end) {const startnode = new node(null, start);const endnode = new node(null, end);let openset = [startnode]; // 存储待检查的节点let closedset = []; // 存储已检查的节点while (openset.length > 0) {console.log('startnode');// 在openset中找到f值最低的节点let lowestindex = 0;for (let i = 0; i < openset.length; i++) {if (openset[i].f < openset[lowestindex].f) {lowestindex = i;}}let currentnode = openset[lowestindex];// 如果当前节点是目的地,那么我们再次构造路径if (currentnode.isequal(endnode)) {let path = [];let current = currentnode;while (current != null) {path.push(current.position);current = current.parent;}return path.reverse(); // 把数组反转,因为我们是从终点回溯到起点存储的}// 当前节点已经被处理过,移出openset,并加入closedsetopenset.splice(lowestindex, 1);closedset.push(currentnode);// 找到所有邻居let neighbors = getneighbors(currentnode, grid);for (let neighbor of neighbors) {// 如果邻居是不可访问的或已在closedset中,忽略它们// 如果这个邻居在关闭列表中,跳过它if (closedset.some(closednode => closednode.isequal(neighbor))) {continue;}// 对角线移动的成本要考虑 √2// 通过查看相邻节点和当前节点的坐标差来判断是否为对角移动const isdiagonalmove =math.abs(currentnode.position[0] - neighbor.position[0]) === 1 &&math.abs(currentnode.position[1] - neighbor.position[1]) === 1;// 对角线移动的成本假定为 √2,其他为1const tentativeg = currentnode.g + (isdiagonalmove ? math.sqrt(2) : 1);// 如果新的g值更低,或者邻居节点不在开放列表中let opennode = openset.find(opennode => opennode.isequal(neighbor));if (!opennode || tentativeg < neighbor.g) {neighbor.g = tentativeg;neighbor.h = heuristic(neighbor, endnode); // h值不变,因为它是启发式估计到终点的成本neighbor.f = neighbor.g + neighbor.h;neighbor.parent = currentnode;// 如果邻居节点不在开放列表中,加入开放列表if (!opennode) {openset.push(neighbor);}}}}// 如果循环结束还没有到达终点,表示没有路径到达终点return [];}
对比上述射线检测的寻路算饭,a*寻路算法的优势比较明显:
-
最优路径保证:a*算法在合适的启发函数(heuristic function)下,保证找到从起点到终点的最短路径,而基于射线检测的方法可能无法始终保证找到最短的路径,尤其是在复杂多变的环境中; -
高效率:a*算法通过启发式评估(即评价函数 f(n) = g(n) + h(n)),能够高效地确定搜索的方向,从而减少需要探索的节点数量。相比之下,基于射线检测的方法可能需要多次尝试和错误,尤其是在遇到多个障碍物时,计算成本较高; 兼容性好:a*算法可以灵活地应用于不同类型的地图和多样化的环境,无论是开放空间、狭窄通道还是复杂迷宫,都能有效工作。通过调整启发式函数,a可以适应各种需求。射线检测方法在一些特定场景(如开阔地带少量障碍)中可能更为直接高效,但在条件复杂的环境中,其性能可能会受到限制。
▐ 简易地图编辑器
实现栅格化
相比于方案一,基于a*的寻路逻辑,需要提前将地图进行栅格化(网格),栅格化是把连续的信息分解成离散的单元格(像素、方格、体素),便于计算处理和分析,我们需要将整张地图进行栅格化,这里是和实际渲染在手机上的地图进行1:1还原,每个单元格以50*50为宽和高,为什么为50,是一个经验值,值越小,鸡走动的约真实,路径就越细致,50已经能满足当前场景。

区块配置、预览
区块指的是地图上的事件的承载体,包含渲染坐标、障碍物坐标、落地点、事件code(服务端关联玩法)等信息。
同时支持运营开发同学自己勾选、编辑、移动障碍物等位置,图中勾选出来的障碍物即为1,不可通行。

如何做到在地图道路上走、和远景房子融合?
这块经过与设计、pd对接,在2d场景下很难实现,我们基于栅格的a*寻路能实现,但是会很不真实,如果要做到该效果,只能做3d的场景,下面是我画的路线图。
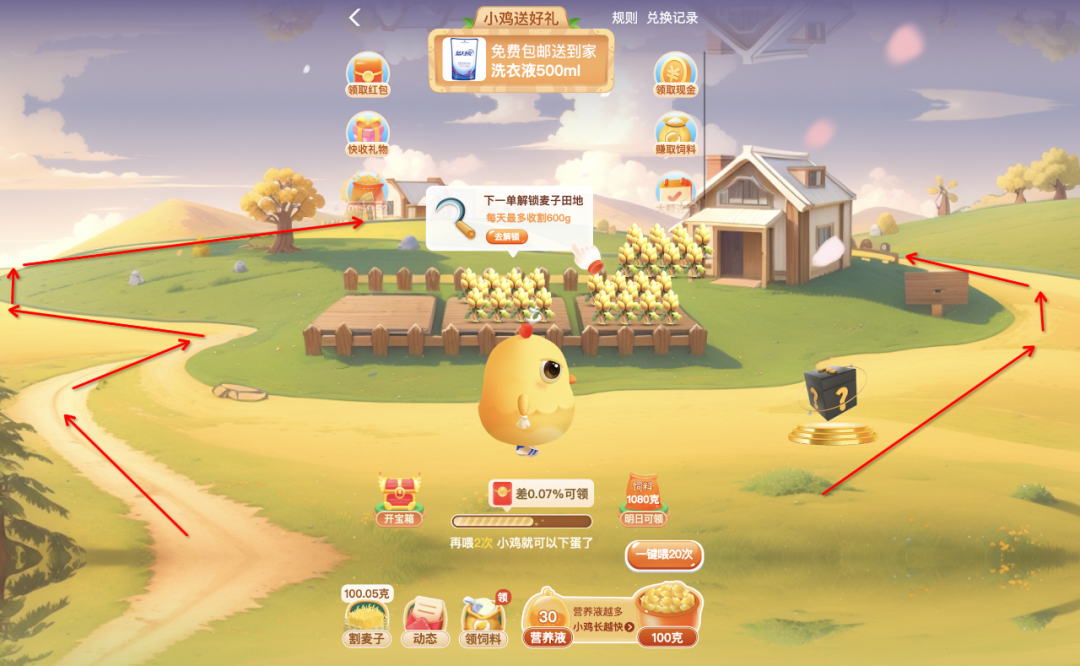
很明显该路线是曲折的,需要小鸡的各角度的侧身,也就是需要x、y、z轴,才能模拟真实的效果,也就是只有3d场景才能满足诉求,与设计同学讨论了一下决定用更适合2d的场景设计,如下图:

我们只需要将障碍物(场景、区块)设置好、在y轴上对小鸡做一定的scale缩放,来做透视扭曲(模拟现实中物体随着距离远近而变化的视觉效果)的效果,就能模拟一定的2.5d效果。

整体将背景结合寻路算法给设计和业务同学看了一下,对于效果还没达到预期,比较僵硬,需要做一些层次效果,来模拟真实走动的效果。
▐ 视差滚动
通过获取相机在x、y轴的滚动距离,与远、中、近景以不同的速率相乘,近景即为草丛区移动得更快,中景即为行动草地区按正常滚动距离移动,远景也就是云层和天空移动得更慢,来模拟摄像机的移动和景深的效果。
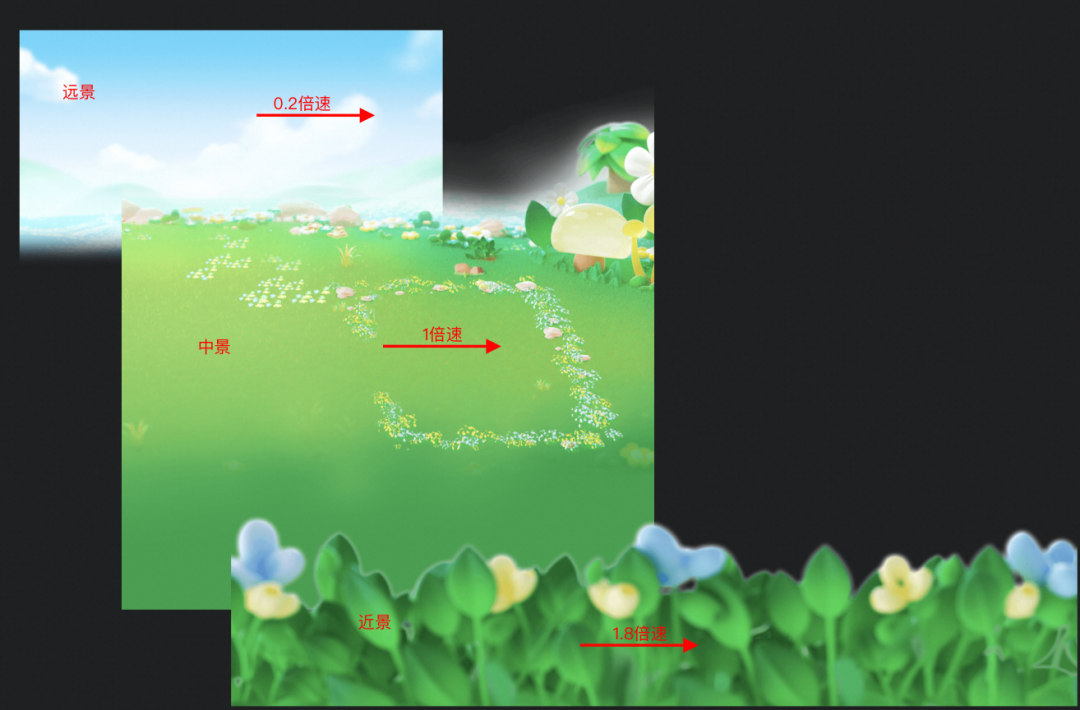
核心代码:
// 远景x轴速率export const parallaxfactorfarx = 0.2;// 远景y轴速率export const parallaxfactorfary = 0.2;// 初始坐标export const faroriginxy = [0, -60];// 近景x轴速率export const parallaxfactornearx = 1.8;// 近景y轴速率export const parallaxfactorneary = 1.05;// 初始坐标export const nearoriginxy = [0, gameheightbounds - 420];const { scrollx, scrolly } = this.scene.cameras.main;if (scrollx >= 0 && scrollx <= 750 && scrolly >= 0 && this.bgfar && this.bgnear) {this.bgfar.x = -scrollx * parallaxfactorfarx;this.bgfar.y = -scrolly * parallaxfactorfary + faroriginxy[1];this.bgnear.x = -scrollx * parallaxfactornearx;this.bgnear.y = -scrolly * parallaxfactorneary + nearoriginxy[1];}
▐ 深度排序
通过调整游戏对象的 depth 值,可以确保某些对象看上去像是位于其他对象的前面或背后,从视觉上产生立体感、模拟真实世界。具体方案为:
-
我们会将当前存在地图上的游戏对象构建虚拟边框,常用矩形去表达,大部分spine对象的形状都是不固定的,面积也会很大,我们统一用矩形去描述游戏对象的轮廓 ; 
-
取每个虚拟边框的bottomy,也就是底边y轴的坐标,按从大到小排序; -
分不同的区间,区间左闭为上一个bottomy,右闭为当前bottomy,生成该区间内可以设置的深度; -
当小鸡行走时,读取y轴坐标,判断在哪一个区间,为小鸡设置该区间可以设置的深度。
核心代码如下:
// 划分区间const divideregional = (blocks: array<{ id: number, bottomy: number }>) => {blocks.sort((a, b) => a.bottomy - b.bottomy);return blocks.map((item, idx) => {const nextbottomy = blocks[idx + 1] ? blocks[idx + 1].bottomy : infinity;return {regional: [(idx + 1) * 100, (idx + 1) * 100 + 100],range: [item.bottomy, nextbottomy],...item}})}// 行走时的判断const currenty = chicken.getposition().y + 130;const currentregion = regionals.find((rengional) => {const [start, end] = rengional.range;return currenty >= start && currenty <= end;})if (currentregion) {chicken.setdepth(currentregion.regional[0] + 1);} else {chicken.setdepth(99);}
▐ 阴影效果
因为我们以2d为主,光照、材质、阴影这块主要是以设计为主:
小鸡 |
神秘屋 |
双色球 |
彩蛋 |
|
|
|
|

全链路指引
主动提的需求,担心用户不知道如何玩儿起来,得提供一个全链路的引导、指引你去熟悉新的玩法,一句话诉求为:用户长时间不行走、没有触发玩法、不浏览地图就触发指引,指引也有一定的优先级。如何划分优先级,这是业务属性,这里就不提了。
第一直觉代码如何编写?
-
在行走结束后启动定时器,在拖拽地图时、触发玩法后清除定时器; -
在拖拽地图结束后启动定时器,在走动、触发玩法后清除定时器; -
在触发玩法后启动定时器,在走动、拖拽地图后清除定时器。
多一个链路,这种像狗皮膏药一样的代码就会越来越多,很不优雅,且容易遗漏。
使用了组内小伙伴做的小而美的多流程定时器的能力,大致的思路如下:
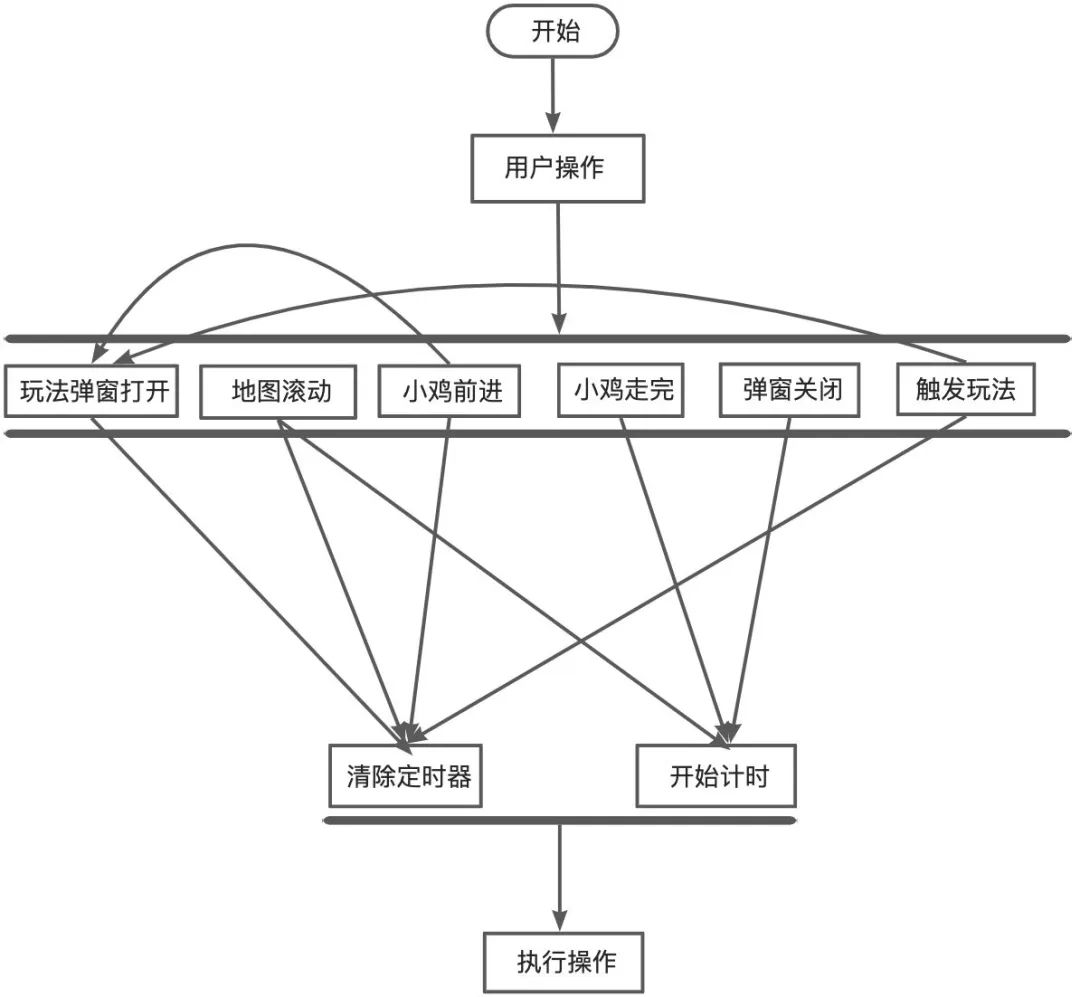
核心思想就是,定时器统一管理,在过程中可以打断和重新计时,只有全部状态ok了,才能执行。
核心代码如下:
function processtimer() {let id = 0;let hasemit = false;const timers = {};const flags = {};const types: any = {};let func: any;const run = (cb) => {func = cb;};const starttimer = (type, delaytime) => {// 触发过或者定时器存在if (hasemit || timers[type]) return;timers[type] = settimeout(() => {flags[type] = true;checktimer();}, delaytime);};const checktimer = () => {const keys = object.keys(timers) || [];const notsatisfied = keys.find((key) => !flags[key]);// 满足所有的条件,出任务触点,只出一次if (!notsatisfied && !hasemit) {hasemit = true;clearalltimer();if (func && typeof func === 'function') {func();}}};const clearalltimer = () => {const keys = object.keys(timers) || [];keys.foreach((key) => {cleartimer(key);});};const cleartimer = (type) => {flags[type] = false;if (timers[type]) {cleartimeout(timers[type]);timers[type] = null;}};const create = (delaytime = 8000) => {const type = `timer${id++}`;timers[type] = null; // 所有定时器flags[type] = false;types[type] = delaytime;return {start: () => {starttimer(type, delaytime);},end: () => {cleartimer(type);},type,};};const reset = () => {hasemit = false;}return {create,run,clearalltimer,reset,};}export default processtimer;

去年写过一篇关于前端业务代码分层的文章《小鸡pk业务架构治理记录》,主要是针对于rax这个视图引擎的,本文的区别在于属于混合开发的模式,phaser游戏开发的内容占比甚至比传统的前端rax/react开发更多。对于我们的分层模式来说其实没什么区别,只不过多了一种渲染方式而已,用phaser渲染和用react还是rax渲染其实都没什么区别。
架构图:
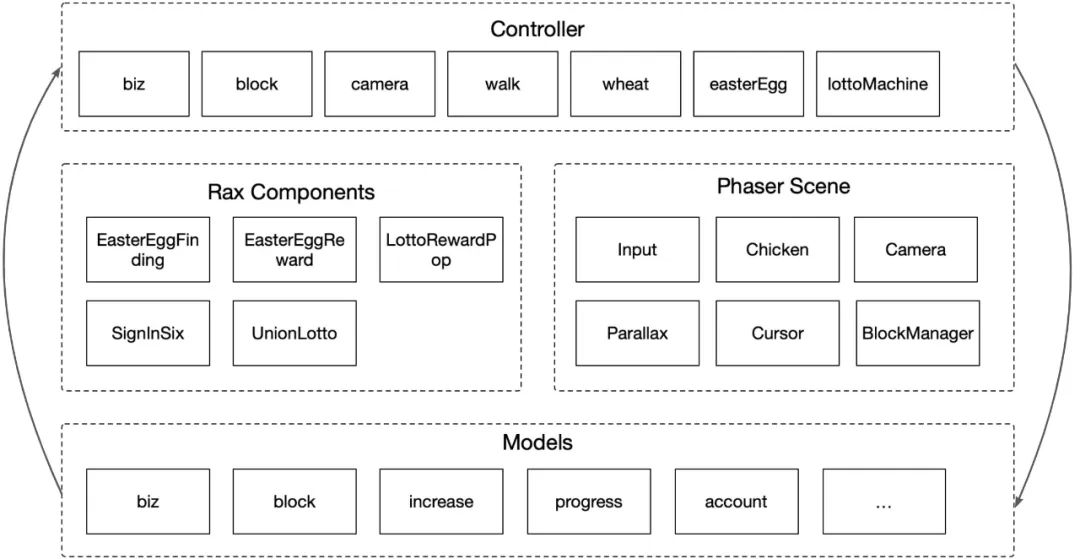
phaser游戏对象设计:

这样设计的好处是游戏对象可以在controller逻辑层任意调用,细看api,游戏对象只负责渲染,不包含任何业务逻辑。

总结
记录一下自己在做这个项目过程中遇到的问题和解决的思路,游戏的开发区别于传统前端,上述一些方案也自己慢慢摸索出来的,有更好的方案也可以一起讨论。

参考资料
-
《spine动画是什么》:https://zhuanlan.zhihu.com/p/679339532 《a*搜索算法简介》:https://zhuanlan.zhihu.com/p/665252967












发表评论