transformers目前大火,但是对于长序列来说,计算很慢,而且很耗费显存。对于transformer中的self attention计算来说,在时间复杂度上,对于每个位置,模型需要计算它与所有其他位置的相关性,这样的计算次数会随着序列长度的增加而呈二次增长。在空间复杂度上,self attention需要存储一个矩阵来保存所有位置的相关性分数,这个矩阵的大小也会随着序列长度的增加而呈二次增长。因此,对于非常长的序列,这种二次复杂度会导致计算和内存消耗急剧增加,使得模型在处理这样的输入时会变得相对缓慢且需要大量内存。这也是为什么对于超长序列,可能需要采取一些策略,如切分成短序列进行处理,或者使用其他模型架构来替代传统的transformer模型。
在pytorch、huggingface transformers library、微软的deepspeed、nvidia的megatron-lm、mosaic ml的composer library、gpt-neox、paddlepaddle中,都已经集成了flash attention。在mlperf 2.1的open division中,在train bert的任务上,flash attention也实现了2.7x的速度提升。
flash attention 1
flash attention 1从attention计算的gpu memory的read和write方面入手来提高attention计算的效率。其主要思想是通过切块(tiling)技术,来减少gpu hbm和gpu sram之间的数据读写操作。通过切块,flash attention1实现了在bert-large(seq. length 512)上端到端15%的提速,在gpt-2(seq. length 1k)上3x的提速。具体数据可看flash attention 1的paper。
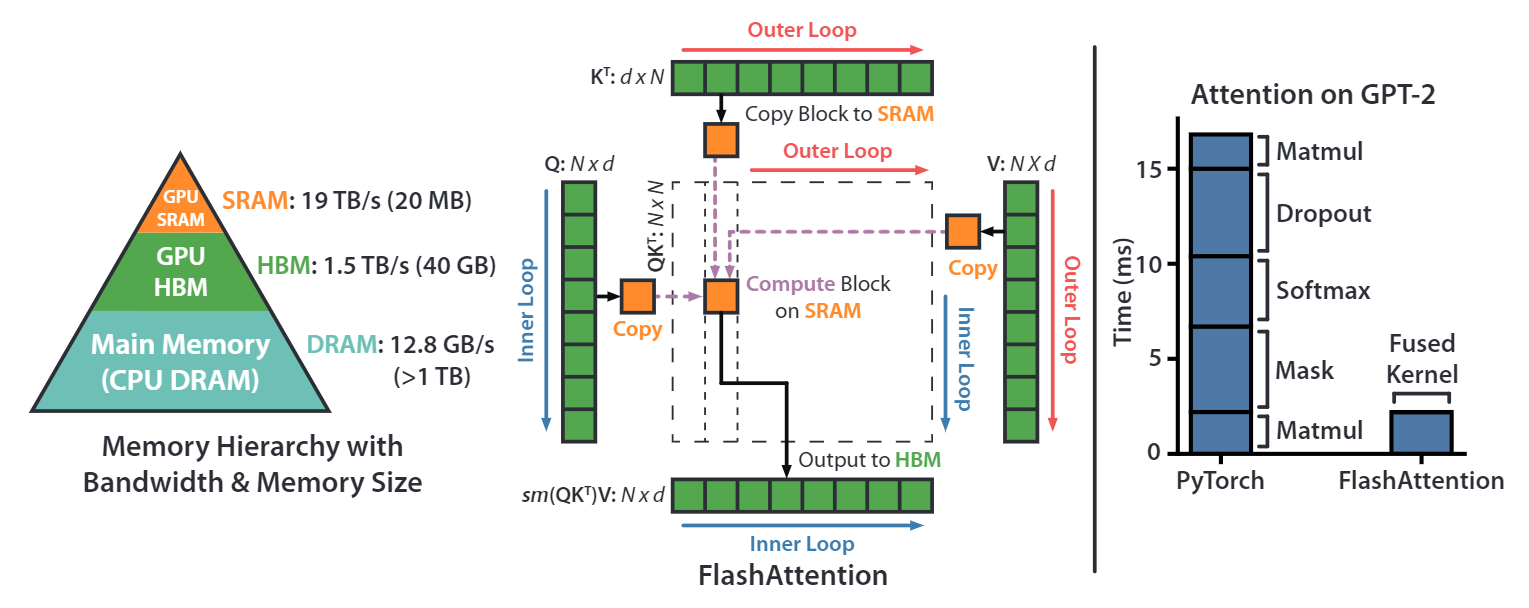
首先我们看一下nvidia gpu的显存架构,上图左图是以nvidia a100 40g显卡为例,我们常说的40g显存是其hbm memory(high bandwidth memory),其带宽是1.5~2.0tb/s,a100上还有一块192kb每108 sm (streaming multiprocessors) 的on-chip sram memory,其带宽是19tb/s。因此,如果能把涉及到显存的读写操作放在sram上,那将会极大的提升速度。
上图中间部分的图描述的就是flash attention 1算法的原理。对于常规的attention计算来说,首先会把q、k和v完整的读进hbm中,然后执行计算。flash attention 1通过将q、k和v切块成很多小块,然后将这些小块的q、k和v放进sram中执行计算,最后再写回hbm中。
上图最右侧图片展示的是通过一些算子融合技术以及flash attention 1的io优化技术,再gpt-2的计算上,flash attention io优化+算子融合,相比pytorch的实现,有大约7.6x的性能提升。

上图的算法流程是标准的attention计算的实现。首先从hbm中加载 q , k q,k q,k矩阵,然后执行 s = q k t s=qk^t s=qkt的计算,将结果 s s s写回hbm;然后将 s s s再从hbm中读取出来,执行 p = s o f t m a x ( s ) p=softmax(s) p=softmax(s)的计算,再将 p p p写回hbm;然后将 p p p和 v v v从hbm中读取出来,执行 o = p v o=pv o=pv的计算,最后把结果写回hbm中。
这个过程中,有多次与hbm的io操作,速度相对较慢。

上图算法流程是flash attention1的forward实现。我们逐步的看一下计算过程。
- 首先根据sram的大小,计算出合适的分块block大小;
- 将 o , l , m o,l,m o,l,m在hbm中初始化为对应shape的全0的矩阵或向量, l , m l,m l,m的具体作用后面算法流程会说明;
- 将 q , k , v q,k,v q,k,v按照分块block的大小切分成许多个blocks;
- 将 o , l , m o,l,m o,l,m也切分成对应数量的blocks;
- 执行outer loop,在outer loop中,做的io操作是将分块的 k j , v j k_j,v_j kj,vj从hbm中加载到sram中;
- 执行inner loop,将 q i , o i , l i , m i q_i,o_i,l_i,m_i qi,oi,li,mi从hbm中load到sram中,然后分块计算上面流程的中间值,在每个inner loop里面,都将 o i , l i , m i o_i,l_i,m_i oi,li,mi写回到hbm中,因此与hbm的io操作还是相对较多的。
由于我们将 q , k , v q,k,v q,k,v都进行了分块计算,而 s o f t m a x softmax softmax却是针对整个vector执行计算的,因此在上图flash attention的计算流程的第10、11、12步中,其使用了safe online softmax技术。
y = s o f t m a x ( x ) y=softmax(x) y=softmax(x)的定义为


上图是naive softmax的实现过程,首先需要迭代计算分母的和,然后再迭代计算vector中每一个值对应的softmax值。这个过程需要两次从内存读取和一次写回内存操作。
但是naive softmax在实际的硬件上计算是有问题的,在naive softmax的实现过程的第3步,由于有指数操作,会有数值溢出的情况,因此在实际使用时,softmax都是使用safe softmax算法
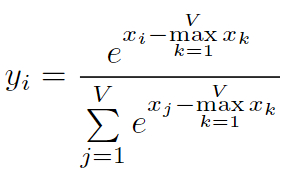

上图是safe softmax的计算过程,其主要修改是在指数部分,减去了要计算vector的最大值,保证了指数部分的最大值是0,避免了数值溢出。在几乎所有的深度学习框架中,都是使用safe softmax来执行softmax算法的。但是safe softmax相比naive softmax,多了一次数据的读取过程,总共是从内存中有三次读取,一次写入操作。
但是不管是naive softmax还是safe softmax,都需要传入一整个vector进行计算,但是flash attention 1算法执行了分块(tiling)策略,导致不能一次得到整个vector,因此需要使用online safe softmax算法。

上面的算法流程是online safe softmax的计算过程。在safe softmax中,vector的最大值 m m m的计算是在一个单独的for循环中,在online safe softmax中, m m m的计算是迭代进行的,因此得到的 m m m不是一个vector中最大的值,而是迭代过程中的局部极大值,相应的对softmax的分母 d d d的计算也要加一个补偿项 e m j − 1 − m j e^{m_{j-1}-m_j} emj−1−mj。
这样得出的结果与直接使用safe softmax是一致的,具体的证明过程可以参考论文online normalizer calculation for softmax。在flash attention 1的算法中,其也使用了online safe softmax,并对其算法进行了相应的扩展。
我们用一个简单的例子看一下safe softmax与pytorch标准的softmax的计算结果。online safe softmax在后面的flash attention的实现中会有体现。
import torch
torch.manual_seed(456)
n, d = 16, 8
q_mat = torch.rand((n, d))
k_mat = torch.rand((n, d))
v_mat = torch.rand((n, d))
# 执行标准的pytorch softmax和attention计算
expected_softmax = torch.softmax(q_mat @ k_mat.t, dim=1)
expected_attention = expected_softmax @ v_mat
## 执行safe softmax和attention计算
# 1st read
s_mat = q_mat @ k_mat.t
row_max = torch.max(s_mat, dim=1).values[:, none]
# 2nd read
input_safe = s_mat - row_max
softmax_numerator = torch.exp(input_safe)
# 3rd read
softmax_denominator = torch.sum(softmax_numerator, dim=1)[:, none]
# 4th read
safe_softmax = softmax_numerator / softmax_denominator
# final matmul (another read / write)
matmul_result = safe_softmax @ v_mat
assert torch.allclose(safe_softmax, expected_softmax)
assert torch.allclose(matmul_result, expected_attention)
经过代码最终的assert,safe_softmax与pytorch标准的softmax的计算结果是一致的。
下面我们用python代码实现flash attention 1的forward算法流程:
import torch
torch.manual_seed(456)
n, d = 16, 8
q_mat = torch.rand((n, d))
k_mat = torch.rand((n, d))
v_mat = torch.rand((n, d))
# 执行标准的pytorch softmax和attention计算
expected_softmax = torch.softmax(q_mat @ k_mat.t, dim=1)
expected_attention = expected_softmax @ v_mat
# 分块(tiling)尺寸,以sram的大小计算得到
br = 4
bc = d
# flash attention算法流程的第2步,首先在hbm中创建用于存储输出结果的o,全部初始化为0
o = torch.zeros((n, d))
# flash attention算法流程的第2步,用来存储softmax的分母值,在hbm中创建
l = torch.zeros((n, 1))
# flash attention算法流程的第2步,用来存储每个block的最大值,在hbm中创建
m = torch.full((n, 1), -torch.inf)
# 算法流程的第5步,执行外循环
for block_start_bc in range(0, n, bc):
block_end_bc = block_start_bc + bc
# line 6, load a block from matmul input tensor
# 算法流程第6步,从hbm中load kj, vj的一个block到sram
kj = k_mat[block_start_bc:block_end_bc, :] # shape bc x d
vj = v_mat[block_start_bc:block_end_bc, :] # shape bc x d
# 算法流程第7步,执行内循环
for block_start_br in range(0, n, br):
block_end_br = block_start_br + br
# 算法流程第8行,从hbm中分别load以下几项到sram中
mi = m[block_start_br:block_end_br, :] # shape br x 1
li = l[block_start_br:block_end_br, :] # shape br x 1
oi = o[block_start_br:block_end_br, :] # shape br x d
qi = q_mat[block_start_br:block_end_br, :] # shape br x d
# 算法流程第9行
sij = qi @ kj.t # shape br x bc
# 算法流程第10行,计算当前block每行的最大值
mij_hat = torch.max(sij, dim=1).values[:, none]
# 算法流程第10行,计算softmax的分母
pij_hat = torch.exp(sij - mij_hat)
lij_hat = torch.sum(pij_hat, dim=1)[:, none]
# 算法流程第11行,找到当前block的每行最大值以及之前的最大值
mi_new = torch.max(torch.column_stack([mi, mij_hat]), dim=1).values[:, none]
# 算法流程第11行,计算softmax的分母,但是带了online计算的校正,此公式与前面说的online safe softmax不一致,但是是同样的数学表达式,只是从针对标量的逐个计算扩展到了针对逐个向量的计算
li_new = torch.exp(mi - mi_new) * li + torch.exp(mij_hat - mi_new) * lij_hat
# 算法流程第12行,计算每个block的输出值
oi = (li * torch.exp(mi - mi_new) * oi / li_new) + (torch.exp(mij_hat - mi_new) * pij_hat / li_new) @ vj
# 算法流程第13行
m[block_start_br:block_end_br, :] = mi_new # row max
l[block_start_br:block_end_br, :] = li_new # softmax denominator
# 算法流程第12行,将oi再写回到hbm
o[block_start_br:block_end_br, :] = oi
assert torch.allclose(o, expected_attention)
运行代码,经过最后的assert操作,没有raise错误,说明通过flash attention计算的o值与pytorch标准的o值是一致的。
flash attention2
flash attention1已经实现了较为显著的性能提升,但是也仅达到了25%~40%的gemm(general matrix multiply)的理论最大flops/s。flash attention的作者通过分析,发现是由于在gpu的不同线程块和warps上的任务切分还不够优化,造成了一些低利用率或者不必要的共享内存的读写操作。进而作者又提出了flash attention2算法,对任务的切分进行了优化,具体来说主要有:(1)调整算法,减少了非矩阵乘法的flops。在深度学习中,通常会使用矩阵乘法运算来进行前向传播和反向传播。这是因为矩阵乘法是一种高效的数值运算,可以在现代硬件上被高效地实现。然而,并不是所有的运算都可以被表示成矩阵乘法的形式。有些运算可能需要使用其他的数值计算方法,这些方法可能会涉及到更多的浮点运算。(2)更大程度的提高了attention计算的并行度,甚至对于单个头的计算,也会将其分发到多个不同的线程块中执行计算,此举相比flash attention1,大约有2x的性能提升。
关于flash attention2对gpu warps的优化调整,flash attention2的论文中有一处说明,如下图所示。

flash attention1的forward计算中,对于每一个block,是将 k , v k,v k,v切分到4个不同的warps(warps 是nvidia gpu并行计算的基本单元。一个warp通常包含32个线程,它们同时执行相同的指令,但对不同的数据进行操作。在gpu执行指令时,通常以warps为单位进行调度,这可以充分利用gpu的并行处理能力)上,但是将 q q q保持为对所有的warps是可见的。关于这样修改为什么会减少shared memory的读写以提高性能,paper的原文是这么说的:

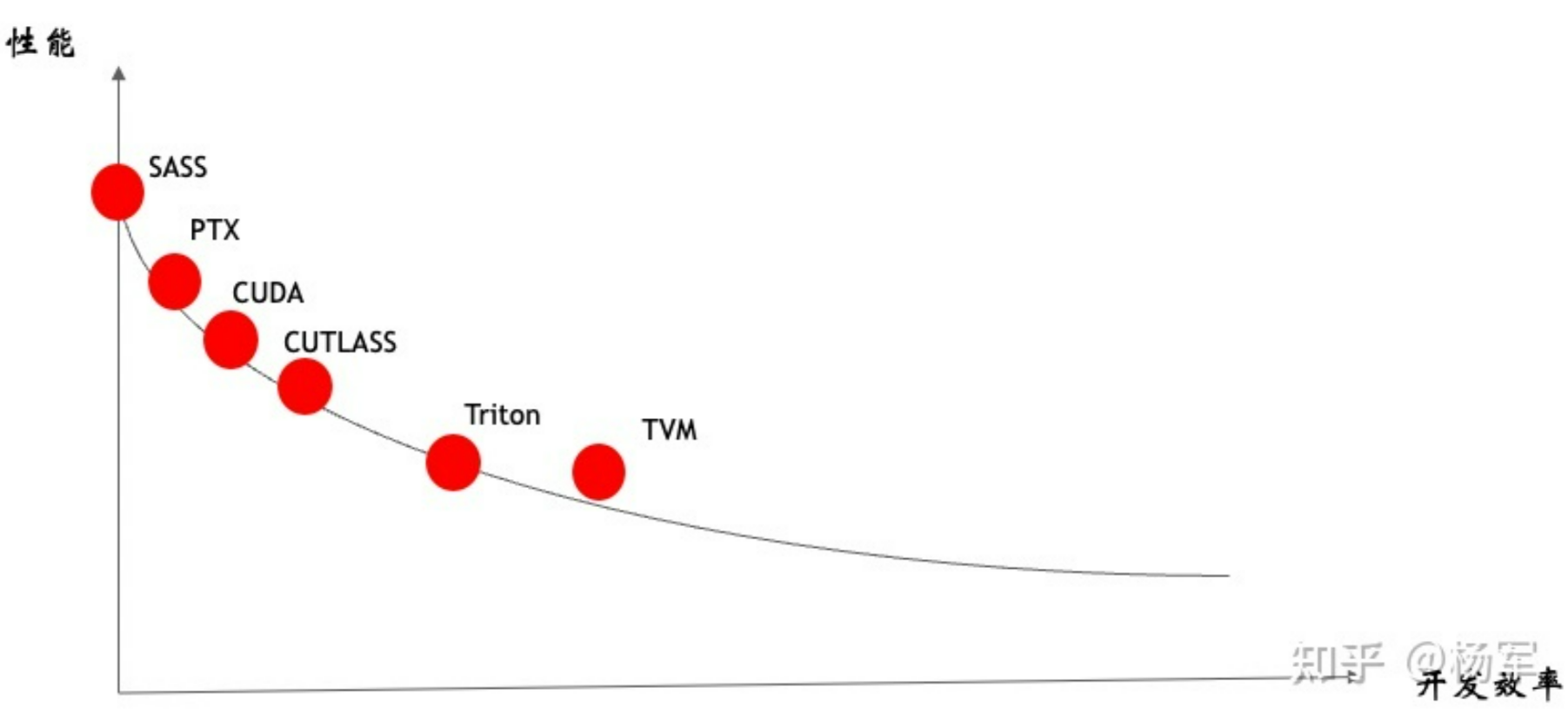
在这里我就不做过多的解释(因为我也不懂,涉及到gpu更底层的实现相关。flash attention是使用cutlass实现的,cutlass相对偏底层,从下图可以看出,cutlass比直接写cuda会更高级一些,但是相比triton,是偏底层)。
下面我们重点放在flash attention2算法的forward计算的实现上。
flash attention2算法的计算流程如下图所示:

flash attention2与flash attention1在算法层面大部分都是相同的,只是少部分地方做了修改,因此我们不做过多的解释,直接通过代码来逐行编程实现。
import torch
torch.manual_seed(456)
n, d = 16, 8
q_mat = torch.rand((n, d))
k_mat = torch.rand((n, d))
v_mat = torch.rand((n, d))
expected_softmax = torch.softmax(q_mat @ k_mat.t, dim=1)
expected_attention = expected_softmax @ v_mat
# 分块(tiling)尺寸,以sram的大小计算得到
br = 4
bc = d
o = torch.zeros((n, d))
# 算法流程第3步,执行外循环
for block_start_br in range(0, n, br):
block_end_br = block_start_br + br
# 算法流程第4步,从hbm中load qi 的一个block到sram
qi = q_mat[block_start_br:block_end_br, :]
# 算法流程第5步,初始化每个block的值
oi = torch.zeros((br, d)) # shape br x d
li = torch.zeros((br, 1)) # shape br x 1
mi = torch.full((br, 1), -torch.inf) # shape br x 1
# 算法流程第6步,执行内循环
for block_start_bc in range(0, n, bc):
block_end_bc = block_start_bc + bc
# 算法流程第7步,load kj, vj到sram
kj = k_mat[block_start_bc:block_end_bc, :]
vj = v_mat[block_start_bc:block_end_bc, :]
# 算法流程第8步
sij = qi @ kj.t
# 算法流程第9步
mi_new = torch.max(torch.column_stack([mi, torch.max(sij, dim=1).values[:, none]]), dim=1).values[:, none]
pij_hat = torch.exp(sij - mi_new)
li = torch.exp(mi - mi_new) * li + torch.sum(pij_hat, dim=1)[:, none]
# 算法流程第10步
oi = oi * torch.exp(mi - mi_new) + pij_hat @ vj
mi = mi_new
# 第12步
oi = oi / li
# 第14步
o[block_start_br:block_end_br, :] = oi
assert torch.allclose(o, expected_attention)
上面的实现只是将算法的计算流程进行了编程实现。但是在实际使用中,会结合gpu的能力进行大规模并行计算。目前大众开发者gpu的编程主要会使用cuda和triton两种语言。cuda语言大家比较熟悉,triton在这里略作介绍。
triton是一种类似 python 的开源编程语言,它能让没有 cuda 经验的研究人员编写高效的 gpu 代码–在大多数情况下与专家编写的cuda代码不相上下。即我们使用 python语言和triton的接口编写完相关计算后,triton编译器会生成高效的cuda代码。triton是openai发布的一项技术,目前国内很多公司也在使用triton生成的cuda代码作为参考。具体的benchmark等信息可以参考openai triton。
下面是flash attention2的triton代码实现。
"""
fused attention
===============
this is a triton implementation of the flash attention v2 algorithm from tri dao (https://tridao.me/publications/flash2/flash2.pdf)
credits: openai kernel team
extra credits:
- original flash attention paper (https://arxiv.org/abs/2205.14135)
- rabe and staats (https://arxiv.org/pdf/2112.05682v2.pdf)
"""
import pytest
import torch
import triton
import triton.language as tl
@triton.jit
def _attn_fwd_inner(
acc, l_i, m_i, q,
k_block_ptr, v_block_ptr,
start_m, qk_scale,
block_m: tl.constexpr,
block_dmodel: tl.constexpr,
block_n: tl.constexpr,
stage: tl.constexpr,
offs_m: tl.constexpr,
offs_n: tl.constexpr,
):
# range of values handled by this stage
if stage == 1:
lo, hi = 0, start_m * block_m
else:
lo, hi = start_m * block_m, (start_m + 1) * block_m
lo = tl.multiple_of(lo, block_m)
k_block_ptr = tl.advance(k_block_ptr, (0, lo))
v_block_ptr = tl.advance(v_block_ptr, (lo, 0))
# loop over k, v and update accumulator
for start_n in range(lo, hi, block_n):
start_n = tl.multiple_of(start_n, block_n)
# -- compute qk ----
k = tl.load(k_block_ptr)
qk = tl.zeros([block_m, block_n], dtype=tl.float32)
qk += tl.dot(q, k)
if stage == 2:
mask = offs_m[:, none] >= (start_n + offs_n[none, :])
qk = qk * qk_scale + tl.where(mask, 0, -1.0e6)
m_ij = tl.maximum(m_i, tl.max(qk, 1))
qk -= m_ij[:, none]
else:
m_ij = tl.maximum(m_i, tl.max(qk, 1) * qk_scale)
qk = qk * qk_scale - m_ij[:, none]
p = tl.math.exp2(qk)
l_ij = tl.sum(p, 1)
# -- update m_i and l_i
alpha = tl.math.exp2(m_i - m_ij)
l_i = l_i * alpha + l_ij
# -- update output accumulator --
acc = acc * alpha[:, none]
# update acc
v = tl.load(v_block_ptr)
acc += tl.dot(p.to(tl.float16), v)
# update m_i and l_i
m_i = m_ij
v_block_ptr = tl.advance(v_block_ptr, (block_n, 0))
k_block_ptr = tl.advance(k_block_ptr, (0, block_n))
return acc, l_i, m_i
@triton.jit
def _attn_fwd(
q, k, v, sm_scale, m, out,
stride_qz, stride_qh, stride_qm, stride_qk,
stride_kz, stride_kh, stride_kn, stride_kk,
stride_vz, stride_vh, stride_vk, stride_vn,
stride_oz, stride_oh, stride_om, stride_on,
z, h,
n_ctx: tl.constexpr,
block_m: tl.constexpr,
block_dmodel: tl.constexpr,
block_n: tl.constexpr,
stage: tl.constexpr,
):
start_m = tl.program_id(0)
off_hz = tl.program_id(1)
off_z = off_hz // h
off_h = off_hz % h
qvk_offset = off_z.to(tl.int64) * stride_qz + off_h.to(tl.int64) * stride_qh
# block pointers
q_block_ptr = tl.make_block_ptr(
base=q + qvk_offset,
shape=(n_ctx, block_dmodel),
strides=(stride_qm, stride_qk),
offsets=(start_m * block_m, 0),
block_shape=(block_m, block_dmodel),
order=(1, 0),
)
v_block_ptr = tl.make_block_ptr(
base=v + qvk_offset,
shape=(n_ctx, block_dmodel),
strides=(stride_vk, stride_vn),
offsets=(0, 0),
block_shape=(block_n, block_dmodel),
order=(1, 0),
)
k_block_ptr = tl.make_block_ptr(
base=k + qvk_offset,
shape=(block_dmodel, n_ctx),
strides=(stride_kk, stride_kn),
offsets=(0, 0),
block_shape=(block_dmodel, block_n),
order=(0, 1),
)
o_block_ptr = tl.make_block_ptr(
base=out + qvk_offset,
shape=(n_ctx, block_dmodel),
strides=(stride_om, stride_on),
offsets=(start_m * block_m, 0),
block_shape=(block_m, block_dmodel),
order=(1, 0),
)
# initialize offsets
offs_m = start_m * block_m + tl.arange(0, block_m)
offs_n = tl.arange(0, block_n)
# initialize pointer to m and l
m_i = tl.zeros([block_m], dtype=tl.float32) - float("inf")
l_i = tl.zeros([block_m], dtype=tl.float32) + 1.0
acc = tl.zeros([block_m, block_dmodel], dtype=tl.float32)
# load scales
qk_scale = sm_scale
qk_scale *= 1.44269504 # 1/log(2)
# load q: it will stay in sram throughout
q = tl.load(q_block_ptr)
# stage 1: off-band
if stage & 1:
acc, l_i, m_i = _attn_fwd_inner(
acc, l_i, m_i, q, k_block_ptr, v_block_ptr,
start_m, qk_scale,
block_m, block_dmodel, block_n,
1, offs_m, offs_n,
)
# barrier makes it easier for compielr to schedule the
# two loops independently
tl.debug_barrier()
# stage 2: on-band
if stage & 2:
acc, l_i, m_i = _attn_fwd_inner(
acc, l_i, m_i, q, k_block_ptr, v_block_ptr,
start_m, qk_scale,
block_m, block_dmodel, block_n,
2, offs_m, offs_n,
)
# epilogue
m_i += tl.math.log2(l_i)
acc = acc / l_i[:, none]
m_ptrs = m + off_hz * n_ctx + offs_m
tl.store(m_ptrs, m_i)
tl.store(o_block_ptr, acc.to(out.type.element_ty))
empty = torch.empty(128, device="cuda")
class _attention(torch.autograd.function):
@staticmethod
def forward(ctx, q, k, v, causal, sm_scale):
# shape constraints
lq, lk, lv = q.shape[-1], k.shape[-1], v.shape[-1]
assert lq == lk and lk == lv
assert lk in {16, 32, 64, 128}
o = torch.empty_like(q)
block_m = 128
block_n = 64 if lk <= 64 else 32
num_stages = 4 if lk <= 64 else 3
num_warps = 4
# tuning for h100
if torch.cuda.get_device_capability()[0] == 9:
num_warps = 8
num_stages = 7 if lk >= 64 else 3
grid = (triton.cdiv(q.shape[2], block_m), q.shape[0] * q.shape[1], 1)
m = torch.empty((q.shape[0], q.shape[1], q.shape[2]), device=q.device, dtype=torch.float32)
_attn_fwd[grid](
q, k, v, sm_scale, m, o,
q.stride(0), q.stride(1), q.stride(2), q.stride(3),
k.stride(0), k.stride(1), k.stride(2), k.stride(3),
v.stride(0), v.stride(1), v.stride(2), v.stride(3),
o.stride(0), o.stride(1), o.stride(2), o.stride(3),
q.shape[0], q.shape[1],
n_ctx=q.shape[2],
block_m=block_m,
block_n=block_n,
block_dmodel=lk,
stage=3,
num_warps=num_warps,
num_stages=num_stages,
)
ctx.save_for_backward(q, k, v, o, m)
ctx.grid = grid
ctx.sm_scale = sm_scale
ctx.block_dmodel = lk
ctx.causal = causal
return o
attention = _attention.apply
我们看上面代码的这部分
p = tl.math.exp2(qk)
l_ij = tl.sum(p, 1)
# -- update m_i and l_i
alpha = tl.math.exp2(m_i - m_ij)
l_i = l_i * alpha + l_ij
# -- update output accumulator --
acc = acc * alpha[:, none]
# update acc
v = tl.load(v_block_ptr)
acc += tl.dot(p.to(tl.float16), v)
# update m_i and l_i
m_i = m_ij
就是算法流程图的按步计算,与我们用纯python实现的过程基本一致。我在实现python版的时,也借鉴了triton版本的相关计算过程。因此也可以发现,triton可以让我们用相对抽象的语言写出高性能cuda代码。下面我们会对triton的实现进行性能benchmark。
然后我们将cutlass实现的flash attention2(flash attention2的默认实现方式)与triton实现的flash attention2进行性能对比。
try:
# flash attention的标准使用接口
from flash_attn.flash_attn_interface import \
flash_attn_qkvpacked_func as flash_attn_func
has_flash = true
except baseexception:
has_flash = false
batch, n_heads, n_ctx, d_head = 4, 48, 4096, 64
# vary seq length for fixed head and batch=4
configs = [
triton.testing.benchmark(
x_names=["n_ctx"],
x_vals=[2**i for i in range(10, 15)],
line_arg="provider",
line_vals=["triton"] + (["flash"] if has_flash else []),
line_names=["triton"] + (["flash-2"] if has_flash else []),
styles=[("red", "-"), ("blue", "-")],
ylabel="ms",
plot_name=f"fused-attention-batch{batch}-head{n_heads}-d{d_head}-{mode}",
args={
"h": n_heads,
"batch": batch,
"d_head": d_head,
"dtype": torch.float16,
"mode": mode,
"causal": causal,
},
)
for mode in ["fwd"]
for causal in [true]
]
@triton.testing.perf_report(configs)
def bench_flash_attention(
batch, h, n_ctx, d_head, causal, mode, provider, dtype=torch.float16, device="cuda"
):
assert mode in ["fwd"]
warmup = 25
rep = 100
if provider == "triton":
q = torch.randn((batch, h, n_ctx, d_head), dtype=dtype, device="cuda", requires_grad=true)
k = torch.randn((batch, h, n_ctx, d_head), dtype=dtype, device="cuda", requires_grad=true)
if mode == "fwd":
q = q.to(torch.float8_e5m2)
k = k.to(torch.float8_e5m2)
v = torch.randn((batch, h, n_ctx, d_head), dtype=dtype, device="cuda", requires_grad=true)
sm_scale = 1.3
fn = lambda: attention(q, k, v, causal, sm_scale)
if mode == "bwd":
o = fn()
do = torch.randn_like(o)
fn = lambda: o.backward(do, retain_graph=true)
ms = triton.testing.do_bench(fn, warmup=warmup, rep=rep)
if provider == "flash":
qkv = torch.randn(
(batch, n_ctx, 3, h, d_head), dtype=dtype, device=device, requires_grad=true
)
fn = lambda: flash_attn_func(qkv, causal=causal)
if mode == "bwd":
o = fn()
do = torch.randn_like(o)
fn = lambda: o.backward(do, retain_graph=true)
ms = triton.testing.do_bench(fn, warmup=warmup, rep=rep)
flops_per_matmul = 2.0 * batch * h * n_ctx * n_ctx * d_head
total_flops = 2 * flops_per_matmul
if causal:
total_flops *= 0.5
if mode == "bwd":
total_flops *= 2.5 # 2.0(bwd) + 0.5(recompute)
return total_flops / ms * 1e-9
# only works on post-ampere gpus right now
bench_flash_attention.run(save_path=".", print_data=true)
在a100上测试,结果如下:
batch4-head48-d64 forward,单位flops/s
| n_ctx(context length) | triton | flash attention2(cutlass) |
|---|---|---|
| 1024 | 123 | 137 |
| 2048 | 159 | 162 |
| 4096 | 163 | 159 |
| 8192 | 167 | 157 |
| 16384 | 167 | 165 |
从前向计算的结果来看,triton的性能在context length较长的情况下,甚至好于cutlass实现的flash attention2。
但是triton实现的flash attention2相比默认使用cutlass实现的,backward计算时,triton的性能大约是cutlass的3/4。后续有机会会补充backward的实现。






发表评论