之前的三篇博客,我们对于哈代温伯格遗传比例有了一个全面的认识,没有看的朋友可以先看一下前面的博客:
1.一些新名词
(1)algorithm: a series of operations executed in a specific order.
算法:按照特定顺序执行的一系列操作。
(2)probability: the chance of an occurrence given repeated attempts.
概率:在重复尝试中发生的可能性。
(3)likelihood: the chance of an occurrence given a model assumption.
可能性:在给定模型假设下发生的机会。
(4)machine learning: a process where computational results are validated to improve accuracy.
机器学习:验证计算结果以提高准确性的过程。
(5)parthenogenesis: development of an embryo without fertilization.
单性生殖:胚胎未经受精而发育。
(6)autogamic: self-fertilizing.
自花授粉:自我受精。
2.期望的偏差(deviation from exception)
在这一点上,我们已经花费了大量时间来验证我们对哈代-温伯格假设下的等位基因频率的期望是否合理。我们可以做出的最有趣的观察之一是,某个种群正在违背我们的期望,当这种情况发生时,我们就可以开始探索其他可能性。在这个探索中,我们可以使用的一个特定的统计工具叫做χ2(卡方)统计检验。我们可以使用这个检验来看我们的观察到的基因型频率是否真的偏离了基于哈代-温伯格预测的期望。关于r语言统计相关的知识,可以看我写的博客:
【r语言从0到精通】-3-r统计分析(列联表、独立性检验、相关性检验、t检验)_r 列联表分析-csdn博客
我们通过一个真实的数据集,该数据集包含了来自尼日利亚拉各斯501人样本的基因型计数(taiwo等人,2011年)。这些是产生血红蛋白的基因的基因型,该基因与镰状细胞贫血症(血红蛋白s)相关。首先,我们计算等位基因和预期基因型频率,然后我们可以对这些数据进行χ2检验。 首先,将每个观察到的基因型计数保存为它们自己的变量。我们将使用aa表示纯合子非镰刀基因型,ss表示纯合子镰刀等位基因基因型,as表示杂合子,三者的和就是总人数n。
| genotyoe | aa | ss | as |
| number | 366 | 12 | 123 |
我们计算镰刀型等位基因s的等位基因频率:
aa <- 366
as <- 123
ss <- 12
n <- aa + as + ss
p <- (ss + (as/2))/n
p![]()
根据观察到的等位基因频率p,我们现在可以计算预期的基因型。因为我们想要追踪两种不同的等位基因(s和a),因此有两种不同的纯合性,我们将ss纯合子定义为p²,而aa纯合子定义为(1-p)²。这里的含义是,只有两种可能的等位基因:s的频率为p,a的频率为非p的所有部分。 现在,通过将我们计算出的基因型频率乘以实际抽样个体的数量,我们可以得到我们预期的个体基因型数量:
expaa <- n*(1-p)^2
expas <- n*2*p*(1-p)
expss <- n*p^2
为了确定我们所看到的基因型数量是否真的符合我们的预期,我们将使用内置的r函数pchisq()来计算来自χ²分布的概率值(p值)。在pchisq()函数中,我们希望将参数lower.tail设置为false,因为我们想看到我们的χ²值高于实际值的概率。随着我们的观察和预期差异越来越大,我们的χ²值应该增加,粗略地说,得到一个非常大的χ²值的概率应该越来越小。
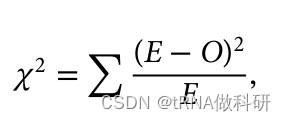
其中e是预期的计数数量,o是观察到的计数数量,这会在所有类别上进行求和。我们希望找到这个χ²统计量在分布中的位置,但为了有一个合适的分布,我们必须告诉函数考虑多少自由度(df)来进行测试。一般来说,我们在计算自由度时,从数据的类别数减一开始,所以在这个例子中有三个类别(expaa、expas和expss)减一。然而,我们还必须从观测数据中估计一个参数p,以生成每个类别的预期值。这意味着我们又失去了一个自由度。因此,df = 3 - 2 = 1(通过从观察数据中估计参数,预期数值“拟合”观察数据更紧密,所以这是有代价的)
chi2 <- (expaa-aa)^2/expaa+
(expas-as)^2/expas+
(expss-ss)^2/expss
pvalue <- pchisq(chi2, df = 1, lower.tail = false)
chi2
pvalue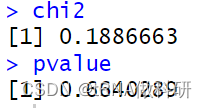
结果得到的p值(0.664>0.5),这表明我们的观察值与预期值相当一致(如果p值小于0.05,则认为一个值与预期显著不同)。因此,这个观察数据似乎完全符合我们从哈代-温伯格预测中所期望的结果。 χ²检验实际上是对似然比检验的一种便捷近似,这种检验被称为g检验或拟合优度检验,也常用于评估模型预测与实际现实世界数据之间的一致性:
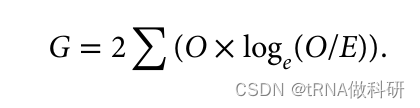
这种方法,顾名思义,关注的是我们的观察值与预期值的似然比。这种g检验方法使用与χ²检验相同的分布,并且表现相似。χ²检验通常被教授而不是g检验,因为它不需要你计算对数值;我们进行稍微更简化的g检验统计量的计算:
geno <- c(aa, as, ss)
expe <- c(expaa, expas, expss)
g <- 2 * sum(geno * log(geno/expe))
pvalue <- pchisq(g, df = 1, lower.tail = false)
g
pvalue

g检验得出的p值(0.668),与χ²检验(0.664)非常相似,因此我们再次相当确信我们的观察数据与我们的预期没有太大差异。
如果你还记得前一章的我们说哈代-温伯格预测的必要条件之一是没有任何遗传变异受到自然选择的影响。在这里,我们处理的等位基因对某一表型有重大影响,例如在纯合子时导致镰刀型贫血,在杂合子时赋予抗疟疾能力,这明显违反了这一假设(luzzatto 2012)。但是,正如我们从刚才分析的血红蛋白s数据中看到的,这些假设经常被违反,然而与哈代-温伯格预期的偏离可能看起来非常小。我们看一个违法的例子:
哈代-温伯格假设之一是每一代配子的有效随机结合,无论潜在的等位基因频率如何。这在克隆物种中严重破坏,其中一个亲本产生一个与自己基因相同的后代。水蚤就是这样一种物种,雌性通常通过孤雌生殖(未受精的卵发育成胚胎)繁殖,一些种群甚至必须进行孤雌生殖(paland等人,2005)
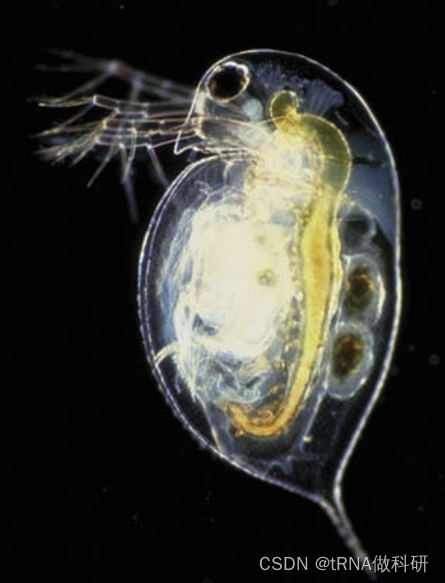
让我们来看一个例子,采集的118只水蚤个体,关于磷酸葡萄糖异构酶(pgi)的两个等位基因,我们再次称之为“a”和“s”,以便我们可以重用之前的代码(hebert和crease 1983)。发现了100个as杂合子和34个aa纯合子,而ss纯合子在样本中完全缺失。我们再次进行卡方检验:
aa <- 34
as <- 100
ss <- 0
n <- aa + as + ss
p <- (ss + (as/2))/n
p
expaa <- n*(1-p)^2
expas <- n*2*p*(1-p)
expss <- n*p^2
chi2 <- (expaa-aa)^2/expaa+
(expas-as)^2/expas+
(expss-ss)^2/expss
pvalue <- pchisq(chi2, df = 1, lower.tail = false)
chi2
pvalue我们得到新的p值:

我们可以看到,这与我们的预期有很大的偏差,p值为5.56×10⁻¹²,我们可以得出结论,pgi基因中的至少一个变体超出哈代-温伯格条件下预期的东西;也就是说,我们没有在每个新世代中随机结合配子。 我们可以使用r函数barplot()将这些数据可视化为条形图。
dat <- matrix(c(geno,expe), nrow = 2, byrow = t)
barplot(dat,beside=t,
col=c("turquoise4", "sienna1"),
names.arg=c("aa", "sa", "ss"))
legend(x="topright", legend=c("observed","expected"),pch=15, col=c("turquoise4","sienna1"))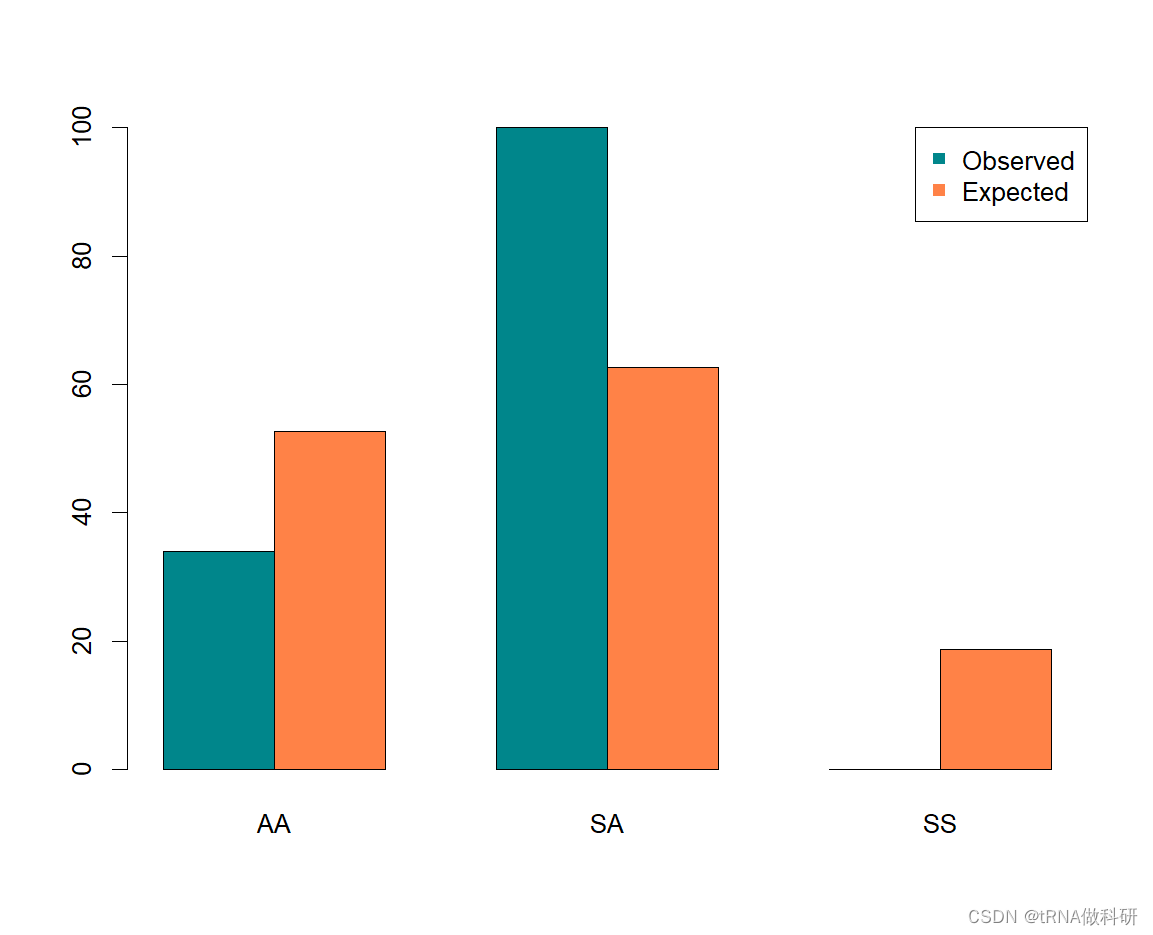
在处理较小的样本量时,考虑使用替代的检验方法可能更为合适,例如“精确检验”(exact test)。在精确检验中,会使用所有可能的等位基因基因型配置来为观察到的配置分配一个p值。关于这一背景下的精确检验的进一步讨论,可以参考guo和thompson(1992年)、wigginton等人(2005年)、engels(2009年)以及其中的参考文献。然而,一般来说,如果样本量足够大,能够检验感兴趣效应的大小,并且不过分关注接近显著性截断边界的结果(例如,johnson 1999年),这些不同的统计方法在最终解释上将会是一致的。
原书内容写的有点不清晰,很多地方重复冗余,我进行提炼总结,许多r语言的错误我也进行了纠正,如果有什么问题,欢迎大家进行讨论。
下一篇博客我们将不只讨论两个等位基因的情况,而是进行一些拓展,下个博客见!







发表评论