智能优化算法应用:基于金枪鱼群算法pid参数优化 - 附代码
摘要:本文主要介绍如何用金枪鱼群算法进行pid参数的优化。
1.pid简介
pid(proportion-integration-differentiation)控 制 器通过比例单元 p、积分单元 i和微分单元 d 的线性组合构成控制量来实现对被控对象的控制,主要适用于基本线性和动态特性不随时间变化的系统。不同的控制规律适用于不同的生产过程,必须合理选择相应的控制规律,否则pid控制器将达不到预期的控制效果当pid控制器采样周期较小时,可以将连续系统离散化,即以一阶差分代替微商,求和代替积分,矩形积分近似代替连续积分,得到如下差分方程:
δ
u
(
t
)
=
k
p
δ
e
(
k
)
+
k
i
δ
e
(
k
)
+
k
d
δ
2
e
(
k
)
(1)
\delta u(t)=k_p \delta e(k) + k_i \delta e(k) + k_d \delta ^2e(k)\tag{1}
δu(t)=kpδe(k)+kiδe(k)+kdδ2e(k)(1)
其中e为输入,
k
p
k_p
kp 为比例系数,
k
i
k_i
ki 为积分时间常数,
k
d
k_d
kd 为微分时间常数。
2.金枪鱼群算法简介
金枪鱼群算法原理请参考:https://blog.csdn.net/u011835903/article/details/123562840
3.适应度函数设计
在此算法中,目标函数设置如下:
f
=
∫
0
∞
(
w
1
∣
e
(
t
)
∣
+
w
2
u
2
(
t
)
)
d
t
(2)
f = \int_{0}^{\infty}(w_1|e(t)|+w_2u^2(t))dt \tag{2}
f=∫0∞(w1∣e(t)∣+w2u2(t))dt(2)
其中, e ( t ) e(t) e(t) 为输入值与输出值之间的误差,考虑到迭代过程的动态特性,采取其绝对值的积分; u ( t ) u(t) u(t) 为控制值,加入此项是为了避免控制幅度过大; w 1 w_1 w1 和 ω 2 ω_2 ω2 为权重,取值范围[0,1]。
此外,还需采取限制措施防止超调,即当出现超调时,在目标函数中额外引入超调项,此时的设置如下:
f
=
∫
0
∞
(
w
1
∣
e
(
t
)
∣
+
w
2
u
2
(
t
)
+
w
3
∣
e
(
t
)
∣
)
d
t
,
e
(
t
)
<
0
(3)
f =\int_{0}^{\infty}(w_1|e(t)| + w_2u^2(t)+w_3|e(t)|)dt,e(t)<0 \tag{3}
f=∫0∞(w1∣e(t)∣+w2u2(t)+w3∣e(t)∣)dt,e(t)<0(3)
其中,
w
3
w_3
w3为权值,且
w
3
>
>
w
1
w_3 >>w_1
w3>>w1 ,一般情况下,
w
1
=
0.999
,
w
2
=
0.001
,
w
3
=
100
w_1 =0.999,w_2 =0.001 , w_3 =100
w1=0.999,w2=0.001,w3=100。
所以金枪鱼群算法的目标就是找到一组pid值,使得f误差最小。
4.算法实验与结果
本文选择二阶系统的传递函数:
g
(
s
)
=
50
/
(
0.125
s
2
+
7
s
)
(4)
g(s) = 50/(0.125s^2+7s) \tag{4}
g(s)=50/(0.125s2+7s)(4)
金枪鱼群算法参数设置如下:
searchagents_no=50; % 种群数量
max_iteration=100; % 设定最大迭代次数
lb = -5; %下边界
ub = 5; %上边界
dim = 3; %维度pid3个参数
s = 1;% 1为单位阶跃响应,其他为正弦输入
fobj = @(x) pid_controller(x,s);%适应度函数
单位阶跃响应寻优结果:
正弦函数输入结果:
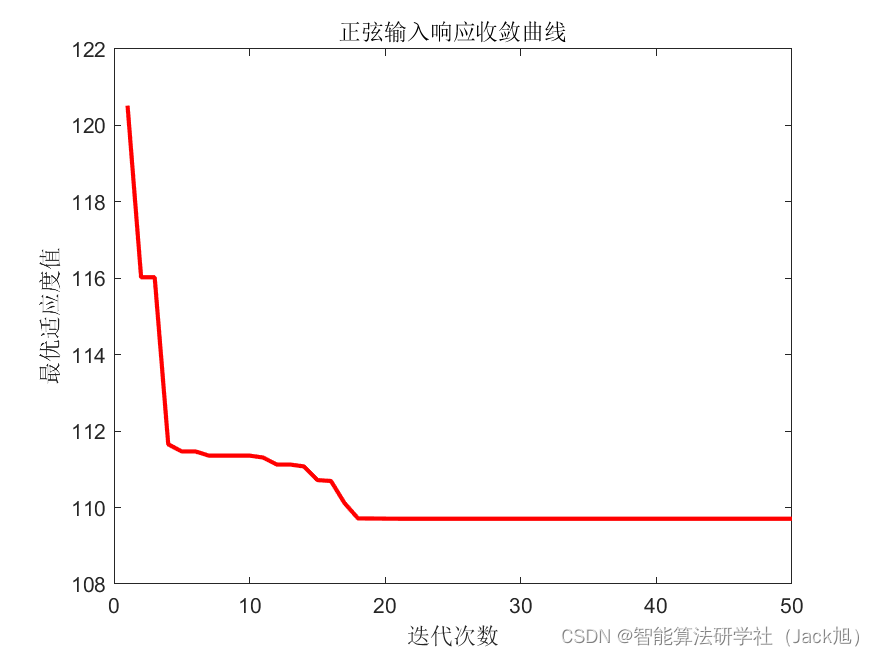
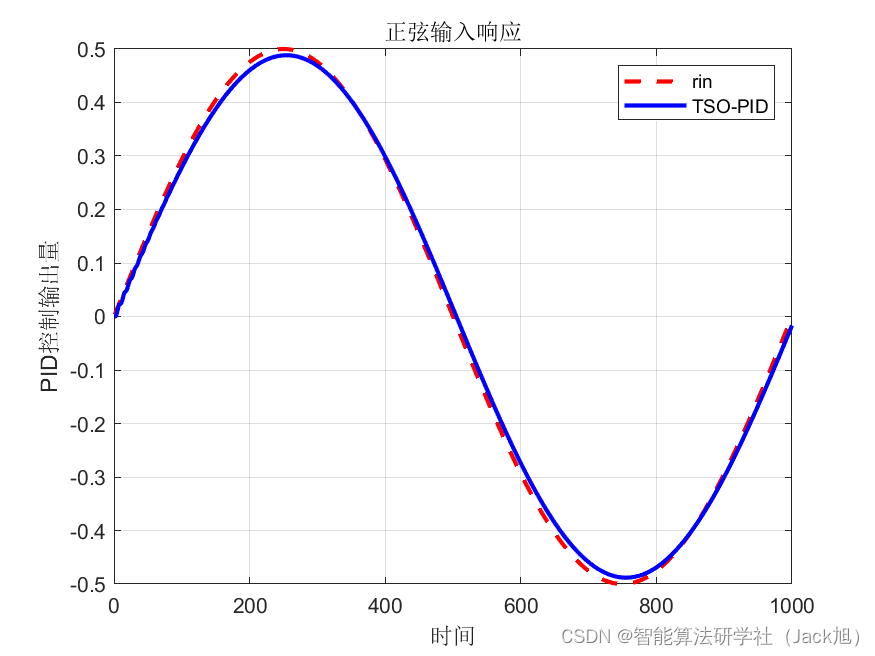
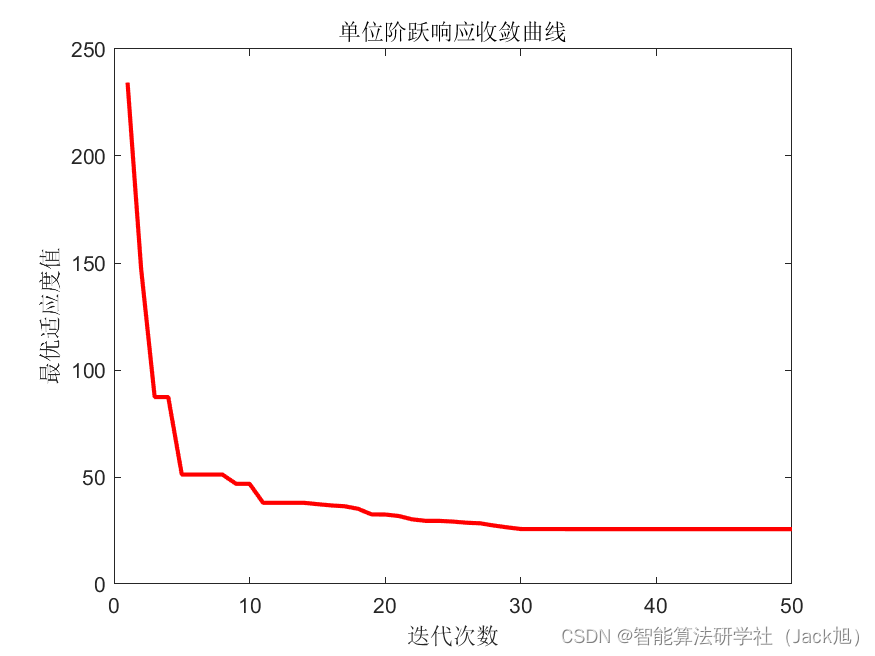
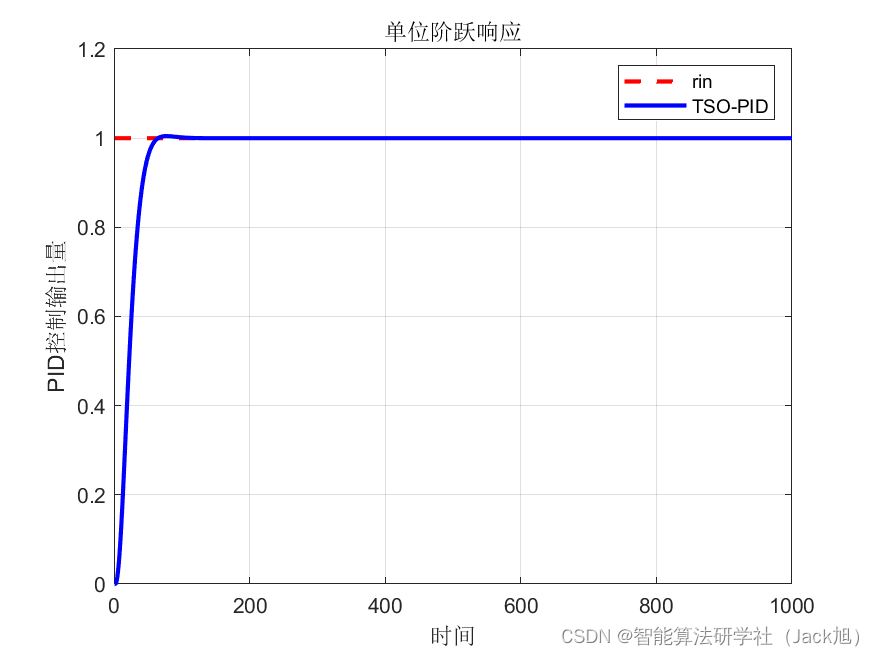
从收敛曲线来看,单位阶跃和正弦输入,算法都在不断寻优。从单位阶跃响应来看,系统上升时间和超调均较小,控制效果明显。从正弦输入结果来看,输入与输出控制量误差较小。
5.参考文献:
[1] 贺圣彦, 曹中清, 余胜威. 基于花授粉算法的pid参数优化[j]. 计算机工程与应用, 2016.






发表评论