目录
1 简介:
聚类是一种无监督学习方法,用于将数据集中的样本划分为具有相似特征的组或簇。聚类的目标是在不事先知道样本的类别标签的情况下,通过发现数据内在的结构和模式,将相似的样本归为一类,并将不相似的样本彼此分开。
聚类算法的工作原理通常是基于样本之间的相似性度量或距离度量。常见的聚类算法包括k均值聚类、层次聚类、dbscan、高斯混合模型等。
2 常见的聚类方法:
当涉及聚类时,可以根据不同的方法和技术来组织数据。下面将介绍划分法、层次法、密度法、图论法、网格法和模型法,并提供每种方法的优点、缺点以及代表性算法。
这些聚类方法在不同的数据集和应用中具有各自的优点和缺点。选择适当的方法取决于数据的特征、问题的要求以及算法的可行性。在实际应用中,可能需要尝试多种方法并进行比较,以获得最佳的聚类结果。
3 欧式空间:
世间万物,皆为混沌。为此,人类世界经历了原始社会、奴隶社会、封建社会、资本主义社会到共产主义社会,这是人类社会从低级到高级的发展过程。但从哲学的角度看来,这实际上是一种从无序到有序的过程。人类社会如此,数学亦是如此。
数字的无穷尽给它的使用带来了极大不便,为此,在一维空间建立了“数轴”,以将这些数字按序列在一条直线上,既便于比较也便于查找与定位,如:𝑥。一维空间最经典的用例,莫过于尺子:用以测量长度。但是地图的出现让人们陷入苦恼,要如何精准地定位一个人的位置呢?“坐标轴”似乎是一个可行的方案:通过在二维平面中,额外增加一条与一维空间中的数轴所垂直的纵向数轴,便能建立一个能海纳百川的空间,此时可用 (𝑥, 𝑦) 定位任意位置。二维空间最典型的用例,莫过于用于进行全球定位的经纬度。在建筑、设计类软件中,处理目标更多的是立体图形,此时,二维空间便显得余力不足。很自然地想到,可采取从一维到二维的相同提升方式,即添加一条与二维平面相垂直的数轴,这样一来就能构建一个涵盖三维空间全部位置的坐标轴,以达到从二维空间到三维空间的提升,此时可用 (𝑥, 𝑦, 𝑧) 定位任意位置。
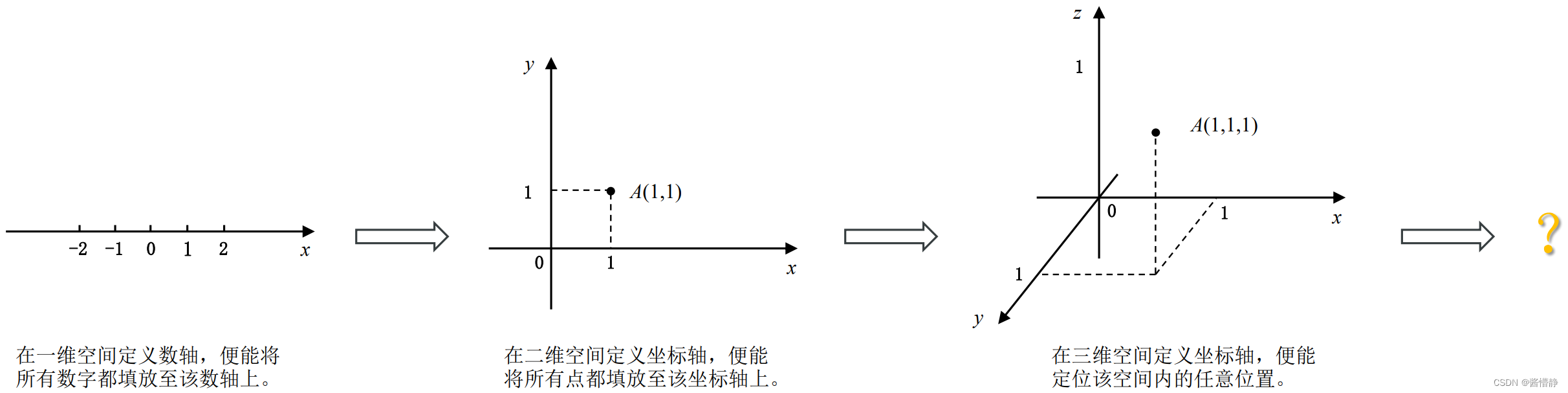
现在让我们回忆下不同空间中与距离相关的一些定义:

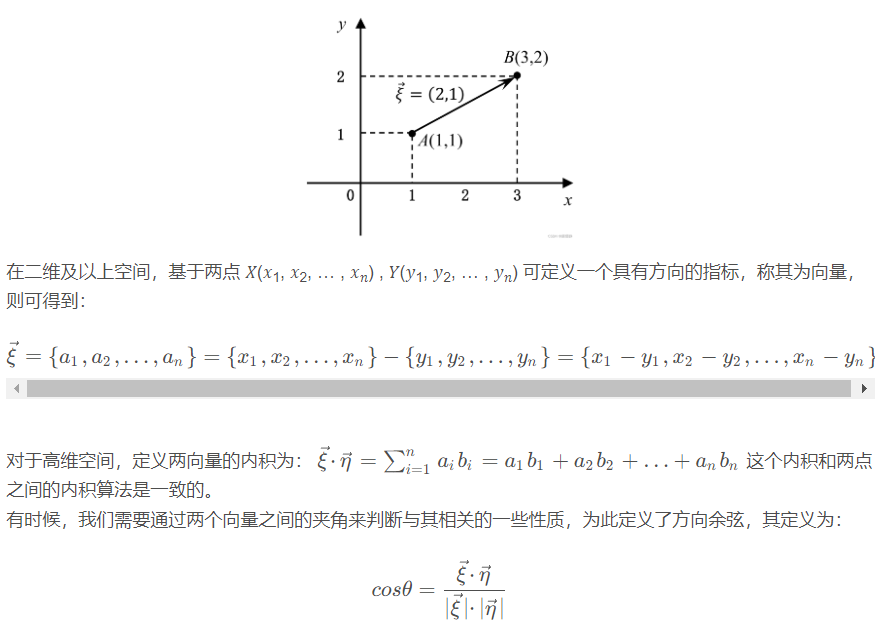
以上就是在低维空间(一维、二维、三维)构建的一系列“秩序”,以帮助我们理解与使用,而高维空间却因它的抽象性显得较有难度。但是,依然可采取与前面的相同的思路来进行拓展。此时,若将在低纬空间总结的有关距离、(内)积、角相关的定理推广至有限的更高维空间,那这些符合定义的空间则被统称为欧几里得空间(亦即欧式空间,euclidean space)。
4 划分法(k-means算法)
4.1 算法思路:
k-means 算法是一种典型的基于划分的聚类算法,它的核心思想是:若将指定数据集的特征投影至 n 维欧氏空间,则数据之间的相似性应当与这些数据的欧氏距离成反比。说简单点就是:越相似的数据,彼此之间离得越近。
其算法流程如下:首先从数据集中随机选取 𝑘 个初始聚类中心 𝐶𝑗 (1 ≤ 𝑗 ≤ 𝑘) (注:该类簇中心不绝对是样本点),接下来对每个其余数据对象,均计算出该数据对象与 𝑘 个聚类中心的的欧式距离,并将离目标数据对象最近的聚类中心 𝐶𝑥 作为该数据对象所属的类别。经过这样一次迭代,就完成了一次 k-means 聚类。接着计算每个簇中数据对象的平均值作为新的聚类中心,进行下一次迭代,直到聚类中心不再变化或达到最大的迭代次数时停止。

上图给出了 k-means 算法的执行流程(通过观察,显然可将该数据集划分为 2 类,因此取 k = 2)
(f) 之后,算法将执行第三次 k-means,接着当再次计算新的类簇中心时,会发现类簇中心不再发生变化(或变化范围很小),此时算法停止并返回最终的分类结果。
总的来看,k-means 算法需要预先指定初始类簇个数和聚类中心,然后再按照样本与类簇中心的距离进行归类与迭代更新。在迭代过程中, k-means 算法会不断降低各类簇的误差平方和sse(sum of squared error,sse),当sse不再变化或目标函数收敛时,聚类结束,得到最终结果。下面给出 k-means 算法计算某个数据对象 𝑥(𝑖) 与某类簇中心 𝐶𝑗 的欧氏距离公式:

4.2 算法总结:
自此,可总结出 k-means 算法的步骤:
① 随机选择 k 个样本作为初始簇类的均值向量
② 将每个样本数据划分给离它距离最近的簇;
③ 根据每个样本所属的簇,更新簇类的均值向量;
④ 重复 ②③ 步,当达到设置的迭代次数或类簇的均值向量不再改变时,模型构建完成,输出聚类算法结果。
k-means 算法非常简单且使用广泛,但是主要存在以下四个缺陷:
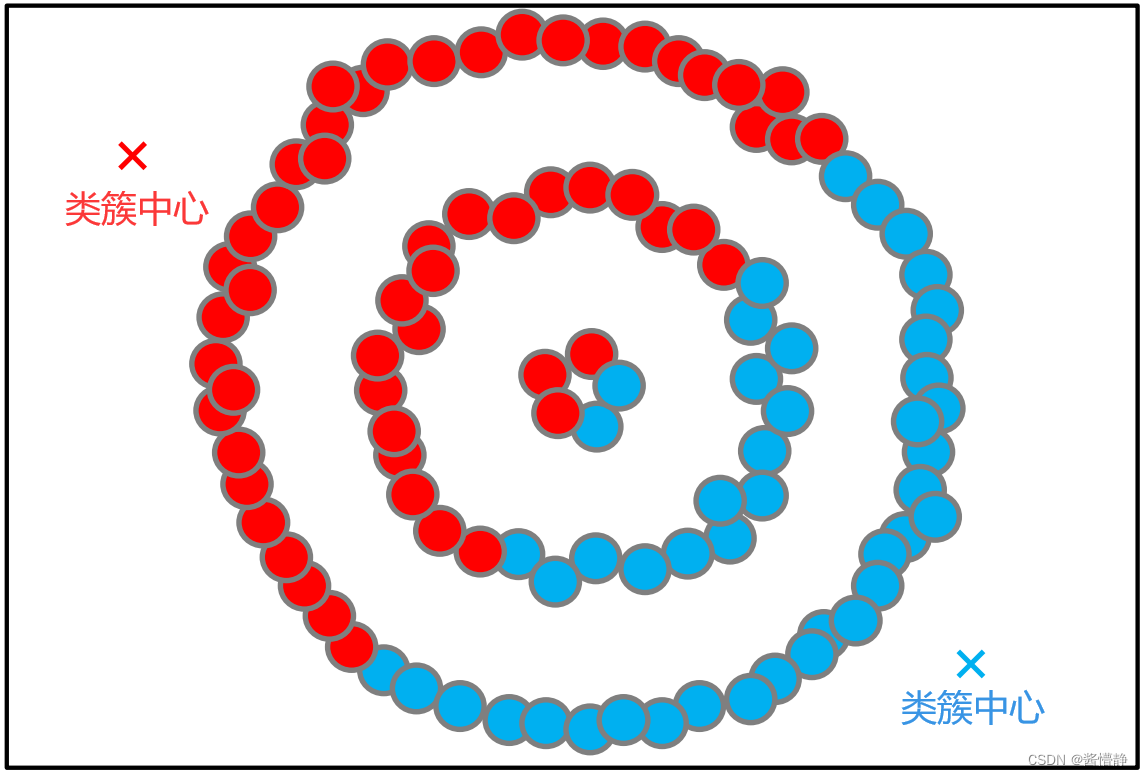
从上图不难看出,k-means算法对于环形簇的分类效果非常糟糕!
4.3 k-means算法的改进:
4.3.1 k-means++算法:
k-means++ 算法是 k-means 算法的改进版,它通过改进初始质心的选择方式,提高了算法的聚类效果。k-means++ 算法的初始质心选择方式是在数据集中随机选择一个点作为第一个质心,然后选择与前面已选质心距离最大的点作为下一个质心,直到选出 k 个质心。与 k-means 算法相比,k-means++ 算法的聚类效果更好,收敛速度更快。
4.3.2 mini-batch k-means 算法:
mini-batch k-means 算法是 k-means 算法的一种变体,它采用了一种随机梯度下降的方式更新质心,从而加速了算法的收敛速度。mini-batch k-means 算法将数据集划分为多个小批量,每个小批量包含一部分数据,然后在每个小批量上执行 k-means 算法,更新质心。与 k-means 算法相比,mini-batch k-means 算法的计算速度更快,但聚类效果可能略有下降。
5 层次法:
当簇具有特定形状(即非平坦流形)且标准欧氏距离不是正确的度量方法时,非平坦几何聚类(non-flat geometry clustering)很有用。
层次聚类就是按类间相似度来一层一层的进行聚类,可以由上向下把大的类别(cluster)分割,叫作分裂法;也可以由下向上对小的类别进行聚合,叫作凝聚法;但是一般用的比较多的是由下向上的凝聚方法。
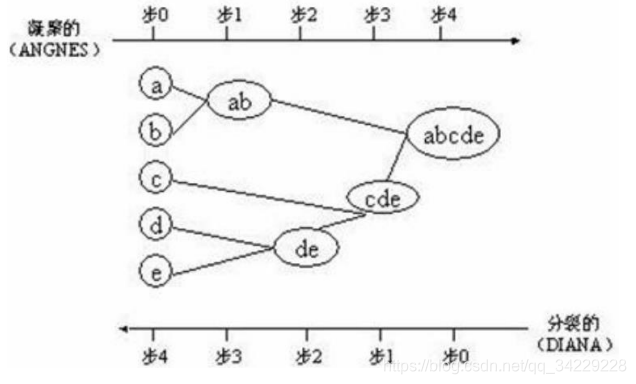
5.1 凝聚层次聚类(agnes)
从一个个单独的数据点开始,不断合并最近的两个聚类簇,直到所有数据点都被合并成一个聚类簇为止。凝聚层次聚类的核心是距离计算和聚类合并规则的选择。常用的距离计算方法有欧几里得距离、曼哈顿距离、余弦距离等。常用的聚类合并规则有最小距离法、最大距离法、重心法等。
下图是层次聚类采用不同的类间距离度量方式的距离结果,其中第二四行的小兰点表示噪声

5.2 分裂层次聚类(diana)
从所有数据点的整体开始,不断将数据点划分成两个或多个子集,直到每个子集都成为一个聚类簇为止。分裂层次聚类的核心是划分方法的选择,常用的划分方法有 k-means、pam 等。 层次聚类算法的优点在于可以自动确定聚类簇的数量和层次结构,但其缺点在于算法的时间复杂度较高,在大数据集上的计算时间可能非常长,并且容易受到噪声数据和异常值的影响。
6 密度法(dbscan聚类):
只要样本点的密度大于某阈值,则将该样本添加到最近的簇中。
- 优点:它能克服"基于距离的聚类算法"只能发现凸聚类的缺点。且密度聚类对噪声不敏感。
- 缺点:计算复杂度高,需建立空间索引降低计算量。
6.1 基本概念:

6.2 算法流程:

密度处理可以去噪。
6.3 调参:
可调参数为m和ε 。从下图可以看出,当m过小,核心对象可能会增多,从而类别数增多。
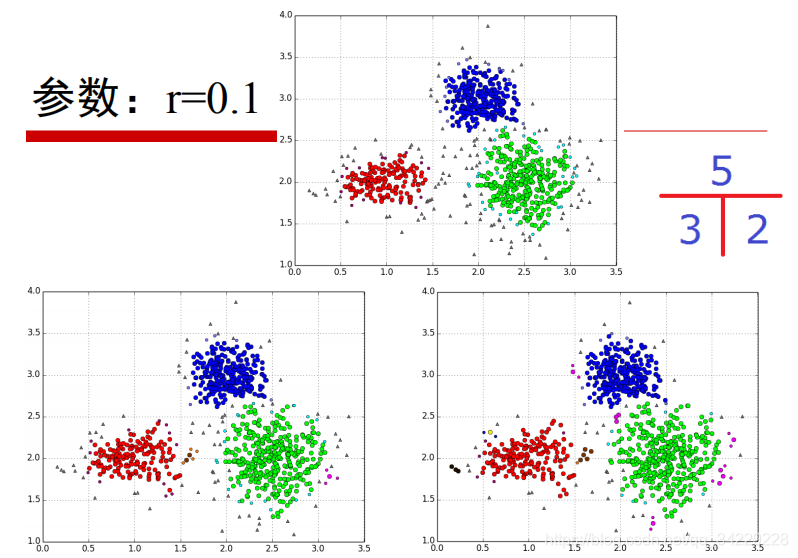
6.4 优缺点:
7 其余的聚类算法:
可以参考下面的一些博客。
8 实战:
8.1 实战一:
8.1.1 目的:
使用 k-means 聚类算法对生成的数据集进行聚类,并使用 calinski-harabasz 分数评估不同聚类数量下的聚类效果
8.1.2 步骤:
8.1.3 代码:
# # api 介绍
# sklearn.cluster.kmeans(n_clusters=8)
# 参数:
# n_clusters:开始的聚类中心数量,整型,缺省值=8,生成的聚类数,即产生的质心(centroids)数。
# 方法:
# estimator.fit(x)
# estimator.predict(x)
# estimator.fit_predict(x) 计算聚类中心并预测每个样本属于哪个类别,相当于先调用fit(x),然后再调用predict(x)
import matplotlib.pyplot as plt
from sklearn.cluster import kmeans
from sklearn.datasets import make_blobs
# 用calinski_harabaz_score方法评价聚类效果的好坏
# 原理是类间距除以类内距,因此这个值越大越好
from sklearn.metrics import calinski_harabasz_score
# 创建数据
# make_blobs 是一个用于生成聚类数据集的函数
# 据集中的样本点具有2个特征,并被分为4个不同的聚类簇。每个聚类簇的中心分别为[-1, -1]、[0, 0]、[1, 1]和[2, 2],并且具有不同的标准差
x, y = make_blobs(n_samples=1000, n_features=2, centers=[
[-1, -1], [0, 0], [1, 1], [2, 2]], cluster_std=[0.4, 0.2, 0.2, 0.2], random_state=9)
x.shape # (1000, 2)
y.shape # (1000,)
# 显示数据集
plt.scatter(x[:, 0], x[:, 1])
plt.show()
# kmeans训练,且可视化 聚类=2
y_predict = kmeans(n_clusters=2, random_state=9).fit_predict(x)
print(y_predict[:10]) # [1 1 0 1 1 0 1 0 1 0]#前10个样本点的分类结果
plt.scatter(x[:, 0], x[:, 1], c=y_predict)
plt.show()
#用于评估聚类结果的指标,用于衡量聚类的有效性和聚类簇的紧密度,越大越好
print(calinski_harabasz_score(x, y_predict)) # 3116.1706763322227
# kmeans训练,且可视化 聚类=3
y_predict = kmeans(n_clusters=3, random_state=9).fit_predict(x)
print(y_predict[:10]) # [0 2 1 2 0 1 2 1 0 1]
plt.scatter(x[:, 0], x[:, 1], c=y_predict)
plt.show()
print(calinski_harabasz_score(x, y_predict)) # 2931.5437780930633
# kmeans训练,且可视化 聚类=4
y_predict = kmeans(n_clusters=4, random_state=9).fit_predict(x)
print(y_predict[:10]) # [3 1 0 1 3 2 1 0 3 2]
plt.scatter(x[:, 0], x[:, 1], c=y_predict)
plt.show()
print(calinski_harabasz_score(x, y_predict)) # 5924.050613480169
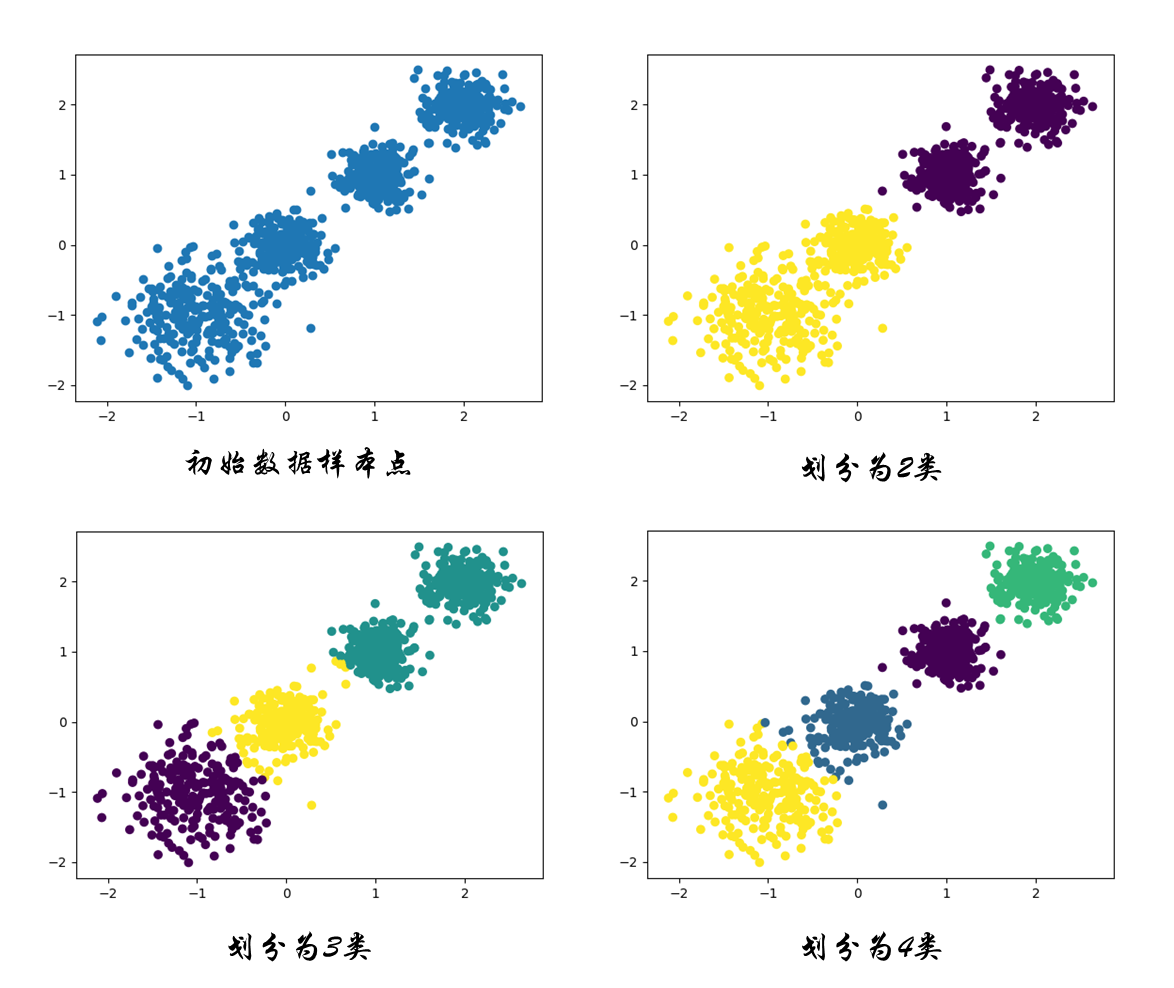
8.2 实战二:
8.2.1 目的:
使用k-means聚类算法对生成的随机数据集进行聚类,并计算聚类结果的calinski-harabasz分数
8.2.2 步骤:
8.2.3 代码:
# 生成随机点
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
x, y_true = make_blobs(n_samples=300, centers=4,
cluster_std=0.60, random_state=0)
plt.scatter(x[:, 0], x[:, 1], s=50)
plt.show()
# k-means 聚类算法
from sklearn.cluster import kmeans
#参数及属性解释
"""
kmeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300,
tol=0.0001, verbose=0, random_state=none, copy_x=true, algorithm='auto')
parameters:
n_clusters: 聚类个数
max_iter: 最大迭代数
n_init: 用不同的质心初始化值运行算法的次数
init: 初始化质心的方法
tol: 关于收敛的参数
random_state: 随机种子
copy_x:是否修改原始数据
algorithm:“auto”, “full” or “elkan”
”full”就是我们传统的k-means算法,
“elkan”elkan k-means算法。默认的
”auto”则会根据数据值是否是稀疏的,来决定如何选择”full”和“elkan”,稠密的选 “elkan”,否则就是”full”
attributes:
cluster_centers_:质心坐标
labels_: 每个点的分类
inertia_:每个点到其簇的质心的距离之和。
"""
m_kmeans = kmeans(n_clusters=4)
from sklearn import metrics
def draw(m_kmeans, x, y_pred, n_clusters):
centers = m_kmeans.cluster_centers_
print("4个类别中心点的坐标为:")
print(centers)
plt.scatter(x[:, 0], x[:, 1], c=y_pred, s=50, cmap='viridis')
# 中心点(质心)用红色标出
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.5)
print("calinski-harabasz score:%lf" % metrics.calinski_harabasz_score(x, y_pred))
plt.title("k-means (clusters = %d)" % n_clusters, fontsize=20)
plt.show()
m_kmeans.fit(x)
kmeans(algorithm='auto', copy_x=true, init='k-means++', max_iter=300,
n_clusters=4, n_init=10, random_state=none, tol=0.0001, verbose=0)
y_pred = m_kmeans.predict(x)
draw(m_kmeans, x, y_pred, 4)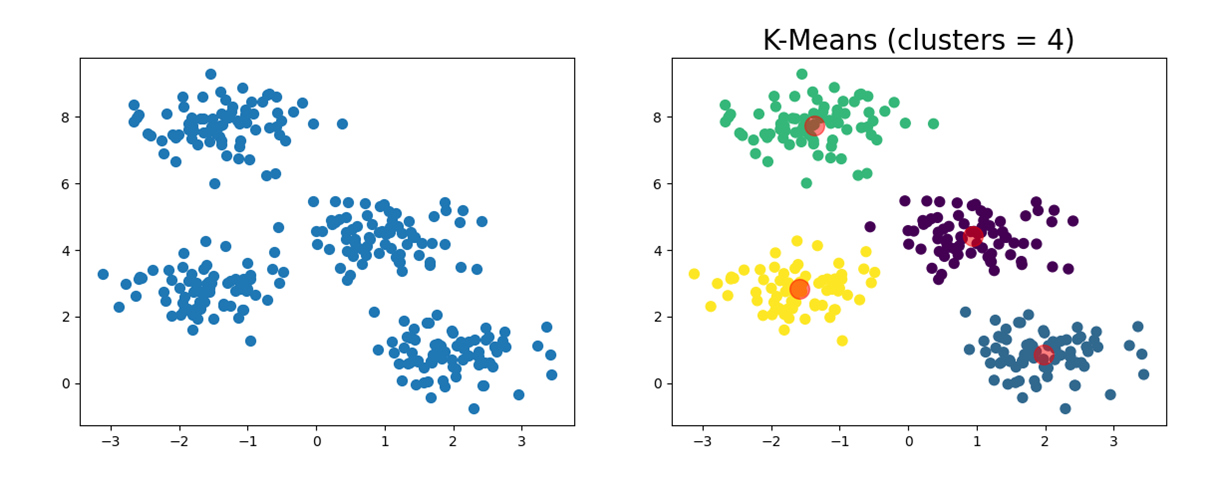


发表评论