目前主流的轨迹跟踪方法有两类:基于几何模型的跟踪方法和基于动力学模型的跟踪方法。
基于几何模型的跟踪方法:
- pure pursuit
- stanley
基于动力学模型的跟踪方法:
- lqr
- mpc
1. 算法思想
前轮反馈控制(front wheel feedback)也就是常说的stanley方法,其核心思想是基于车辆前轴中心点的路径跟踪偏差量对方向盘转向控制量进行计算。
stanley方法是一种基于横向跟踪误差(前轴中心b到规划轨迹最近点c的距离)的非线性反馈函数,并且能实现横向跟踪误差收敛到0。
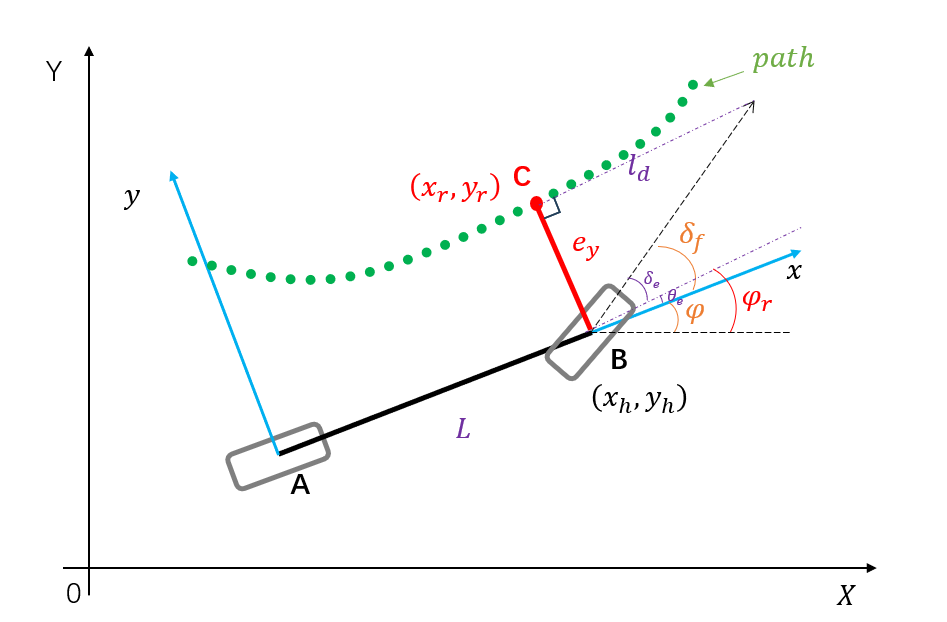
图中,
| 大地坐标系 | x 0 y |
|---|---|
| 车身坐标系 | x 0 y |
| 全局路径下的规划轨迹 | path |
| 前轮转角 | δ f \delta{{}}{}_{{f}} δf |
| 自车航向角 | φ \varphi φ |
| 轨迹航向角 | φ r \varphi_r φr |
| 预瞄距离 | l d l_d ld |
| 横向误差 | e y e_y ey |
| 轴距 | l |
| 规划轨迹最近点c | ( x r , y r ) \left({{x}}{}_{{r}},{{y}}{}_{{r}}\right) (xr,yr) |
| 自车前轴中心a | ( x h , y h ) \left({{x}}{}_{{h}},{{y}}{}_{{h}}\right) (xh,yh) |
根据车辆位姿与规划轨迹的相对几何关系可以直观的获得前轮转角的目标值,前轮转角 δ f \delta{{}}{}_{{f}} δf由两部分构成:
-
航向误差引起的转角 δ φ \delta{{}}{}_{{\varphi}} δφ,即规划轨迹最近点的切线方向与车身坐标系x轴的 夹角 δ φ \delta{{}}{}_{{\varphi}} δφ
根据上图的几何关系,在不考虑横向跟踪误差(或横向误差为0)的情况下,前轮偏角和给定路径切线方向一致,所以航向误差引起的转角:
δ φ = φ r − φ \delta{{}}{}_{{\varphi}} = \varphi_{r} -\varphi δφ=φr−φ
其中, φ r \varphi_{r} φr 表示规划轨迹的航向角, φ \varphi φ表示自车的航向角。 -
横向误差引起的转角 δ e \delta{{}}{}_{{e}} δe,即规划轨迹最近点的切线方向与前轮速度方向的夹角 δ e \delta{{}}{}_{{e}} δe
根据上图的几何关系,在不考虑航向跟踪偏差(或航向误差为0)的情况下,横向跟踪误差越大,前轮转向角越大,位置误差引起的转角:
δ e = arctan e y l d \delta _{e} =\arctan \frac{e_{y} }{l_{d} } δe=arctanldey
l d l _{d} ld是人为给定的一个预瞄距离,通常认为和速度正相关:
l d = v k l _{d} =\frac{v}{k } ld=kv
代入,得到位置误差引起的转角:
δ e = arctan k e y v \delta _{e} =\arctan \frac{ke_{y} }{v } δe=arctanvkey
综上,得到stanley算法总的前轮转角:
δ
f
=
δ
φ
+
δ
e
\delta{{}}{}_{{f}} = \delta{{}}{}_{{\varphi}} + \delta{{}}{}_{{e}}
δf=δφ+δe
算法本质
使用线性自行车模型,横向误差变化率可以通过下式计算:
e
y
˙
=
−
v
sin
δ
e
\dot{e_{y} }=-v\sin \delta _{e}
ey˙=−vsinδe
其中
sin
δ
e
\sin \delta _{e}
sinδe根据几何关系可知:
sin
δ
e
=
e
y
l
d
2
+
e
y
2
\sin \delta _{e}=\frac{e_{y} }{\sqrt{{l_{d}} ^{2} +{e_{y}}^{2} } }
sinδe=ld2+ey2ey
将
l
d
l _{d}
ld带入
sin
δ
e
=
k
e
y
v
2
+
k
e
y
2
\sin \delta _{e}=\frac{{k}e_{y} }{\sqrt{{v} ^{2} +{{k}e_{y}}^{2} } }
sinδe=v2+key2key
所以,得到横向误差:
e
y
˙
=
−
k
v
e
y
v
2
+
k
e
y
2
=
−
k
e
y
1
+
(
k
e
y
v
)
2
\dot{e_{y} }=\frac{{-kv}e_{y} }{\sqrt{{v} ^{2} +{{k}e_{y}}^{2} } } =\frac{{-k}e_{y} }{\sqrt{1 +{\left ( \frac{{k}e_{y}}{v} \right ) }^{2} } }
ey˙=v2+key2−kvey=1+(vkey)2−key
当横向误差很小时,忽略二次项,上式可以近似写成:
e
y
˙
≈
−
k
e
y
\dot{e_{y} }\approx {-k}e_{y}
ey˙≈−key
对左右两边进行积分,得到横向误差的表达式:
e
y
(
t
)
=
e
y
(
0
)
×
e
−
k
t
e_{y}\left ( t \right ) =e_{y}\left ( 0 \right )\times e ^{-kt}
ey(t)=ey(0)×e−kt
可以看出,当
t
⟶
∞
t\longrightarrow \infty
t⟶∞时,横向误差以指数形式收敛于 0,而参数
k
k
k决定了收敛速度。
2. 代码实现
3. pure pursuit与stanley 算法对比
- pure pursuit 基于对前轮转角进行控制来消除横向误差,本质是基于一个基于横向误差的p控制器。所以纯跟踪算法从原理上讲是无法消除航向误差的,而且这里的横向误差是指预瞄点的横向误差,即使横向误差为0,也无法保证自车前轴或后轴或质心处的横向误差为0;
- stanley 基于对前轮转角进行控制来消除横向误差和航向误差。由于是基于前轮中心进行的控制,理论上讲是可以将自车前轴中心的横向误差和航向误差都消除至0的;
- pure pursuit算法的关键在于预瞄点的选取:其距离越短,控制精度越高,但可能会产生震荡;预瞄距离越长,控制效果趋于平滑,震荡减弱。实际调试只需根据上述规则以及应用需求调整预瞄系数即可。
- stanley 算法的控制效果取决于控制增益,它缺少pure pursuit算法的规律性,调试时需要花一定精力去寻找合适的控制增益值。


发表评论