前言
通过本文可以了解到
- 什么是图像的距离?
- 什么是距离变换
- 距离变换的计算
- opencv中距离变换的实现
什么是图像的距离?
距离(distance)是描述图像两点像素之间的远近关系的度量,常见的度量距离有欧式距离(euchildean distance)、城市街区距离(city block distance)、棋盘距离(chessboard distance)。
- 欧式距离
欧式距离的定义源于经典的几何学,与我们数学中所学的简单几何的两点之间的距离一致,为两个像素点坐标值得平方根。欧式距离的优点在于其定义非常地直观,是显而易见的,但缺点在于平方根的计算是非常耗时的。
de = sqrt(((x2 - x1)*(x2 - x1) + (y2 - y1)*(y2 - y1)));
- 城市街区距离
城市街区距离也称d4距离,此距离描述的是只允许像素坐标系平面中横向和纵向的移动距离,4表示在这种定义下,像素点是4邻接的,即每个点只与它的上、下、左、右相邻的4个点之间的距离为1。其定义为
d4 = abs(x1 - x2) + abs(y1 - y2);
- 棋盘距离
如果允许在图像坐标系中像素点的对角线方向的移动,就可以得到棋盘距离,也称d8距离,8表示在这种定义下,像素点是8邻接的,即每个点只与它的上、下、左、右、四个对角线方向相邻的8个点之间的距离为1。
d8 = max(abs(x1 - x2), (y1 - y2));
图1表示了三个距离之间的关系
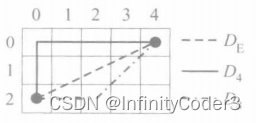
图1 三种距离示意图
什么是距离变换?
图2是一个简单距离转换的例子,使用的棋盘距离
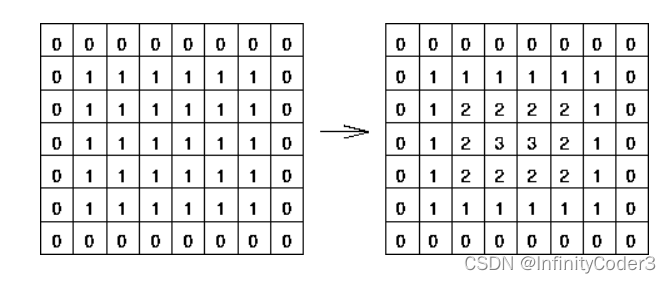
图2 棋盘距离变换例子
距离变换算法步骤
直观计算
确定了距离公式之后,根据直观的理解应该怎么计算呢?还是拿上面的例子进行说明,b代表着黑色背景的集合,里面有b1, b2, b3……等一些点;w代表着白色物体的集合,里面有w1,w2,w3……等一些点。现在我们就是要计算w集合里面的每一个点,到b集合的距离,那么我们就每一次取一个w里面的wi,然后根据距离公式,计算wi到b集合每一个点bj的距离dij,取其中距离dij 最小的值,作为最后的度量结果,直到w集合的每一个点都计算一遍。实际上,在进行计算距离这一步之前,还要遍历图像把像素点分成两个集合,这种直观的计算相对来说,较复杂且花费时间较长,因此前人发明一种快速计算距离变换的方法。
快速计算
对于欧式距离变换算法,相关学者研究了速度更快的倒角距离变换算法,来近似欧式距离变换的效果。具体过程如下:
- 使用前向模板如图3中左边
3*3模板,对图像从上到下,从左到右进行扫描,模板中心0点对应的像素值如果为0则跳过,如果为1则计算模板中每个元素与其对应的像素值的和,分别为sum1,sum2,sum3,sum4,sum5,而中心像素值为这五个和值中的最小值。 - 使用后向模板如图fig.3中右边的
3*3模板,对图像从下到上,从右到左进行扫描。 - 一般我们使用的倒角距离变换模板为
3 * 3和5 * 5,分别如下图所示:
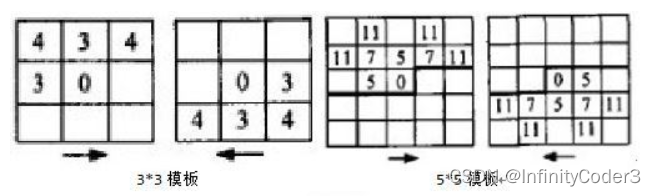
图3 倒角距离变换模板
示例
al al
al p mask1
al
br
p br mask2
br br
- 将图像进行二值化,子图像值为0,背景为255;
- 利用mask 1从左向右,从上到下扫描,p点是当前像素点,q点是mask 1中al邻域中的点,d为距离计算,包括棋盘距离、城市距离和欧式距离。fp为p点的像素值,计算
f(p) = min( f(p), f(q)+d(p,q) ), 其中,q属于al.
- 再利用mask 2从右向左,从下向上扫描,计算
f(p) = min( f(p), f(q)+d(p,q) ), 其中,q属于br.
代码实现距离变换算法
void imageprocess::distancetransform(const cv::mat& src_image, cv::mat& dst_image)
{
//step1: check the input parameters: 检查输入参数
assert(!src_image.empty());
assert(src_image.channels() == 1);
//step2: initialize dst_image : 初始化目标图像
cv::threshold(src_image, dst_image, 100, 255, cv::thresh_binary);
//step3: pass throuth from top to bottom, left to right: 从上到下,从做到右遍历
for (size_t i = 1; i < dst_image.rows - 1; i++)
{
for (size_t j = 1; j < dst_image.cols; j++)
{
//al al
//al p
//al
std::array<cv::point, 4> al;
al.at(0) = cv::point( i - 1, j - 1 );
al.at(1) = cv::point( i - 1, j );
al.at(2) = cv::point( i, j - 1 );
al.at(3) = cv::point(i + 1, j - 1 );
int fp = dst_image.at<uchar>(i, j);
//fq
std::array<int, 4> fq = { 0 };
fq.at(0) = dst_image.at<uchar>(i - 1, j - 1);
fq.at(1) = dst_image.at<uchar>(i - 1, j);
fq.at(2) = dst_image.at<uchar>(i, j - 1);
fq.at(3) = dst_image.at<uchar>(i + 1, j - 1);
std::array<int, 4> dpq = { 0 };
std::array<int, 4> dpqaddfq = { 0 };
for (size_t k = 0; k < 4; k++)
{
//d(p, q)
dpq.at(k) = d4(i, al.at(k).x, j, al.at(k).y);
//d(p,q) + f(q)
dpqaddfq.at(k) = dpq.at(k) + fq.at(k);
}
//f(p) = min[f(p), d(p,q) + f(q)]
std::sort(dpqaddfq.begin(), dpqaddfq.end());
auto min = dpqaddfq.at(0);
fp = std::min(fp, min);
dst_image.at<uchar>(i, j) = fp;
}
}
//step4: pass throuth from bottom to top, right to left: 从下到上,从右到左遍历
for (int i = dst_image.rows - 2; i > 0; i--)
{
for (int j = dst_image.cols - 2; j >= 0 ; j--)
{
// br
// p br
// br br
std::array<cv::point, 4> br;
br.at(0) = cv::point( i - 1, j + 1 );
br.at(1) = cv::point( i , j + 1 );
br.at(2) = cv::point( i + 1, j + 1 );
br.at(3) = cv::point( i + 1, j );
int fp = dst_image.at<uchar>(i, j);
//fq
std::array<int, 4> fq = { 0 };
fq.at(0) = dst_image.at<uchar>(i - 1, j + 1);
fq.at(1) = dst_image.at<uchar>(i, j + 1);
fq.at(2) = dst_image.at<uchar>(i + 1, j + 1);
fq.at(3) = dst_image.at<uchar>(i + 1, j);
std::array<int, 4> dpq = { 0 };
std::array<int, 4> dpqaddfq = { 0 };
for (size_t k = 0; k < 4; k++)
{
//d(p, q)
dpq.at(k) = d4(i, br.at(k).x, j, br.at(k).y);
//d(p,q) + f(q)
dpqaddfq.at(k) = dpq.at(k) + fq.at(k);
}
//f(p) = min[f(p), d(p,q) + f(q)]
std::sort(dpqaddfq.begin(), dpqaddfq.end());
auto min = dpqaddfq.at(0);
fp = std::min(fp, min);
dst_image.at<uchar>(i, j) = static_cast<uchar>(fp);
}
}
}
int imageprocess::d4(const int& x1, const int& x2, const int& y1, const int& y2)
{
return abs(x1 - x2) + abs(y1 - y2);
}
int imageprocess::d8(const int& x1, const int& x2, const int& y1, const int& y2)
{
return cv::max(abs(x1 - x2), (y1 - y2));
}
opencv distancetransform函数
- 函数签名
/** @overload
@param src 8-bit, single-channel (binary) source image.
@param dst output image with calculated distances. it is a 8-bit or 32-bit floating-point,
single-channel image of the same size as src .
@param distancetype type of distance, see #distancetypes
@param masksize size of the distance transform mask, see #distancetransformmasks. in case of the
#dist_l1 or #dist_c distance type, the parameter is forced to 3 because a \f$3\times 3\f$ mask gives
the same result as \f$5\times 5\f$ or any larger aperture.
@param dsttype type of output image. it can be cv_8u or cv_32f. type cv_8u can be used only for
the first variant of the function and distancetype == #dist_l1.
*/
cv_exports_w void distancetransform( inputarray src, outputarray dst,
int distancetype, int masksize, int dsttype=cv_32f);
参数详解:
- inputarray src:输入图像,一般为二值图像;
- outputarray dst:输出的图像,距离变换结果,灰度图;
- int distancetype:用于距离变换的距离类型(欧氏距离:dist_l2 = 2; d 4 d_4 d4距离:dist_l1 = 1; d 8 d_8 d8距离:dist_c = 3等);
- int mask_size:距离变换掩模的大小,一般为3或5;
- int dsttype:输出图像的数据类型,可以为cv_8u或cv_32f。
测试代码
#include<opencv2/opencv.hpp>
using namespace cv;
using namespace std;
int main()
{
//初始化输入图像和变换结果图像
mat mat(480, 480, cv_8uc1, scalar(0)), transmate, transmatd4, transmatd8;
//给输入图像指定三个像素点作为距离变换原点(区域块)
mat.at<uchar>(100, 200) = 1;
mat.at<uchar>(200, 100) = 1;
mat.at<uchar>(300, 300) = 1;
//将将输入图像中1和0调换,使得原点距离为0
mat = 1 - mat;
//显示原始图像(显示为黑色)
imshow("原始图片", mat);
//分别利用欧式距离、d4距离和d8距离作距离变换,将结果存入transmatd4、transmatd8和transmate
distancetransform(mat, transmate, dist_l2, 0);
distancetransform(mat, transmatd4, dist_l1, 0, cv_8u);
distancetransform(mat, transmatd8, dist_c, 0);
//欧式距离与d8距离作变换后,值为32位浮点数,以下代码将其值转为uchar类型
transmate.convertto(transmate, cv_8u);
transmatd8.convertto(transmatd8, cv_8u);
//显示距离变换结果
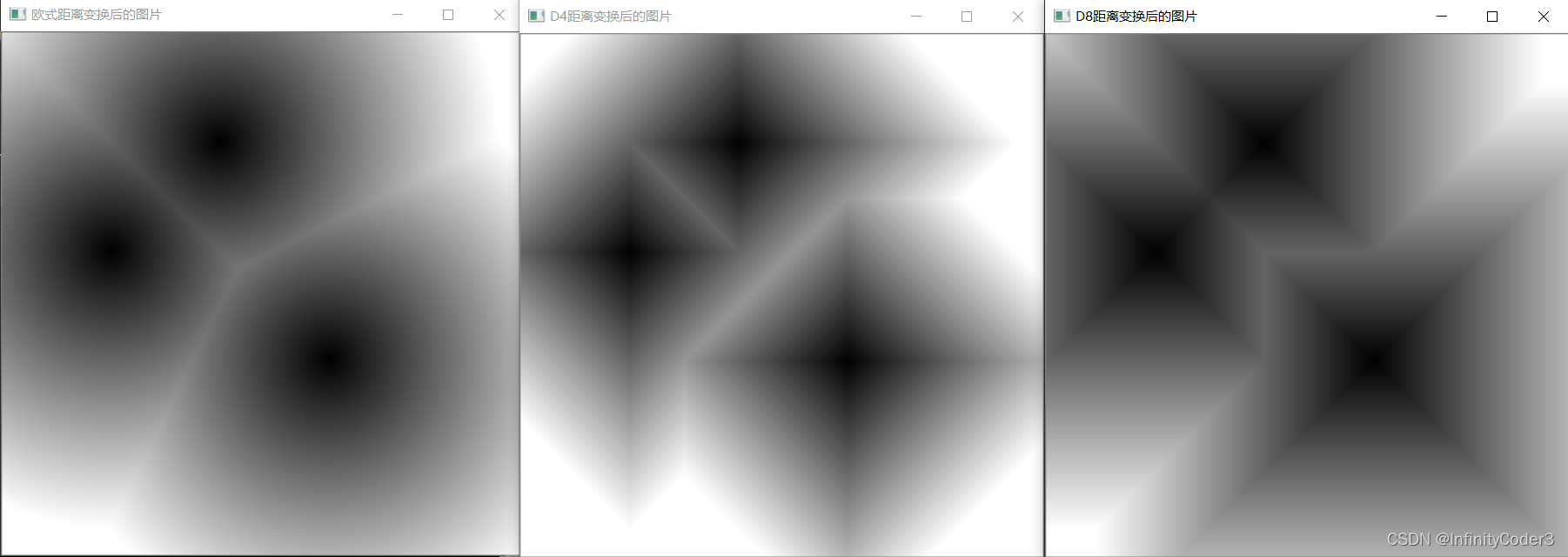
imshow("欧式距离变换后的图片", transmate);
imshow("d4距离变换后的图片", transmatd4);
imshow("d8距离变换后的图片", transmatd8);
waitkey();
return 0;
}
运行结果



发表评论