| 题目 | 类型 |
|---|---|
| 1、背包问题求具体方案数 | 背包问题方案数量 |
| 2、有依赖的背包问题 | 有依赖的背包问题 |
| 3、能量石 | 贪心+dynamic programming |
| 4、金明的预算方案 | 有依赖的背包问题 |
1、背包问题求具体方案数
思路:
01背包+背包dp输出方案
为了输出背包dp方案,我们可以把整个状态转移的过程看成一个拓扑图
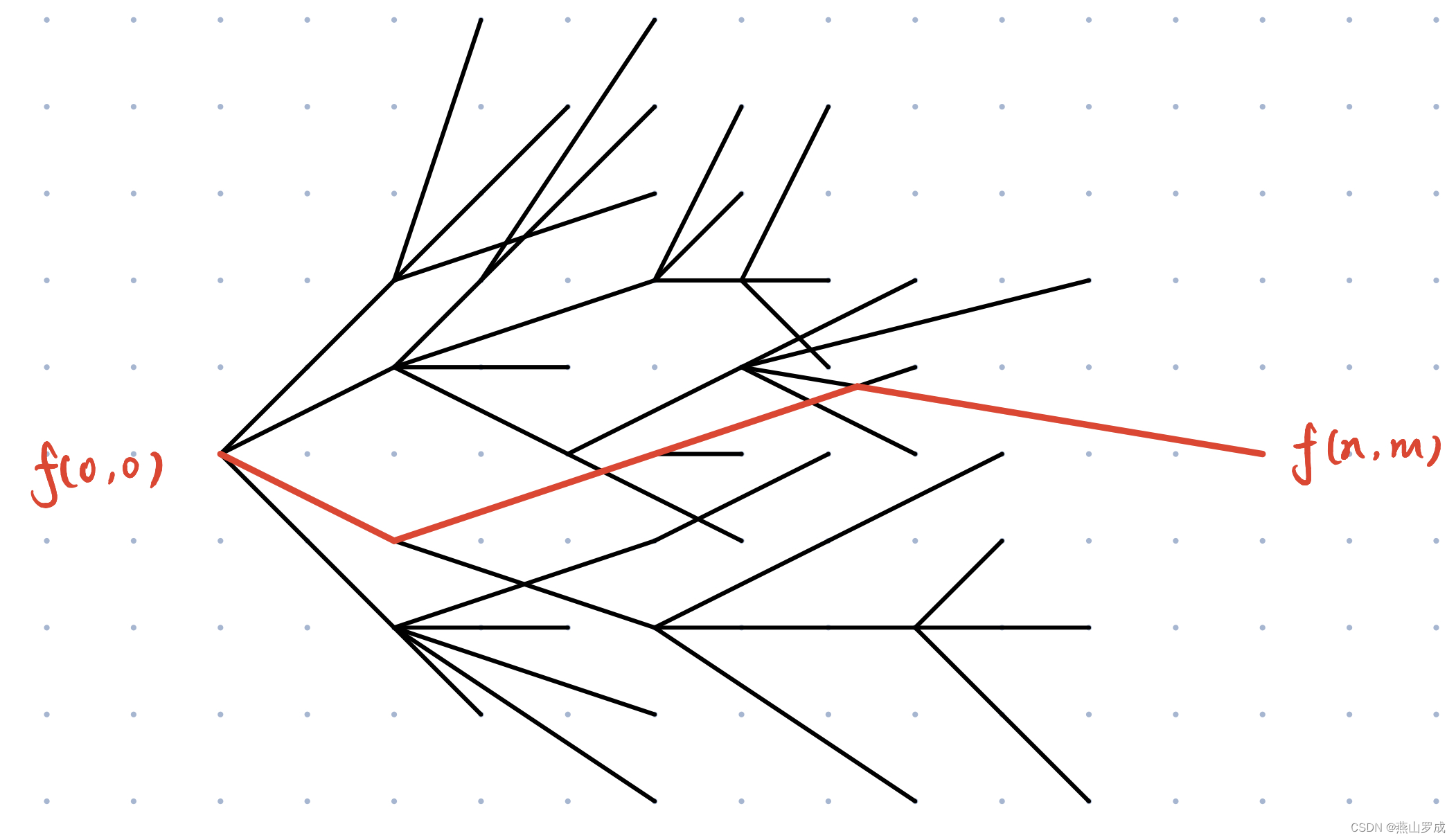
可以从最后一个状态倒推到初始状态,就可以输出方案了:
for (int i = 1, j = m; i <= n; ++ i)
{
if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
{
path[cnt ++ ] = i;
j -= v[i];
}
}
for (int i = 0; i < cnt; ++ i) cout << path[i] << " ";
代码:
#include <iostream>
using namespace std;
const int n = 1010;
int n, m;
int w[n], v[n];
int f[n][n];
int path[n], cnt;
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
for (int i = n; i >= 1; -- i)
{
for (int j = 0; j <= m; ++ j)
{
f[i][j] = f[i + 1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
}
}
for (int i = 1, j = m; i <= n; ++ i)
{
if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
{
path[cnt ++ ] = i;
j -= v[i];
}
}
for (int i = 0; i < cnt; ++ i) cout << path[i] << " ";
cout << endl;
return 0;
}
2、有依赖的背包问题
>
>输入格式 第一行有两个整数 n,v ,用空格隔开,分别表示物品个数和背包容量。
>
> 接下来有 n 行数据,每行数据表示一个物品。 第 i 行有三个整数 vi,wi,pi
> ,用空格隔开,分别表示物品的体积、价值和依赖的物品编号。 如果 pi=−1 ,表示根节点。 数据保证所有物品构成一棵树。
>
> 输出格式 输出一个整数,表示最大价值。
>
>
> 数据范围 1≤n,v≤100
>
> 1≤vi,wi≤100 父节点编号范围:
>
> 内部结点:1≤pi≤n;
>
> 根节点 pi=−1;
>
> 输入样例
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2
> 输出样例: 11
思路:
dfs在遍历到 v[x] 结点时,一定选上根节点 x ,所以初始化 f[x][v[x] ~ m] = w[x]
j 的范围 [ v[x],m] 因为要放下根节点
k 的范围 [ 0 , j-v[x] ],也因为要放下根节点
f[x][v]表达选择以x为子树的物品,在体积不超过v时所获得的最大价值
代码:
#include<bits/stdc++.h>
using namespace std;
const int n=103;
const int v=103;
int w[n],v[n];
vector<int>g[n];
int n,m,root;
int f[n][n];
void dfs(int x)
{
for(int i=v[x];i<=m;i++)f[x][i]=w[x];
for(int i=0;i<g[x].size();i++)
{
int y=g[x][i];
dfs(y);
for(int j=m;j>=v[x];j--)
{
for(int k=0;k<=j-v[x];k++)
{
f[x][j]=max(f[x][j],f[x][j-k]+f[y][k]);
}
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
int father;
cin>>v[i]>>w[i]>>father;
if(father==-1)root=i;
else g[father].push_back(i);
}
dfs(root);
cout<<f[root][m];
return 0;
}
3、能量石
> 输入格式 第一行包含整数 t ,表示共有 t 组测试数据。
>
> 每组数据第一行包含整数 n ,表示能量石的数量。
>
> 接下来 n 行,每行包含三个整数 si,ei,li 。
>
> 输出格式 每组数据输出一个结果,每个结果占一行。
>
> 结果表示为 case #x: y,其中 x 是组别编号(从 1 开始),y 是可以获得的最大能量值。
>
> 数据范围 1≤t≤10 , 1≤n≤100 , 1≤si≤100 , 1≤ei≤105 , 0≤li≤105
输入样例:
3
4
20 10 1
5 30 5
100 30 1
5 80 60
3
10 4 1000
10 3 1000
10 8 1000
2
12 300 50
5 200 0
输出样例:
case #1: 105
case #2: 8
case #3: 500
样例解释 在样例#1中,有 n=4 个宝石。杜达可以选择的一个吃石头顺序是:
>
> 吃第四块石头。这需要 5 秒,并给他 80 单位的能量。 吃第二块石头。这需要 5 秒,并给他 5 单位的能量(第二块石头开始时具有
> 30 单位能量,5 秒后失去了 25 单位的能量)。 吃第三块石头。这需要 100 秒,并给他 20
> 单位的能量(第三块石头开始时具有 30 单位能量,10 秒后失去了 10 单位的能量)。 吃第一块石头。这需要 20 秒,并给他 0
> 单位的能量(第一块石头以 10 单位能量开始,110 秒后已经失去了所有的能量)。 他一共获得了 105
> 单位的能量,这是能获得的最大值,所以答案是 105 。
>
> 在样本案例#2中,有 n=3 个宝石。
>
> 无论杜达选择吃哪块石头,剩下的两个石头的能量都会耗光。
>
> 所以他应该吃第三块石头,给他提供 8 单位的能量。
>
> 在样本案例#3中,有 n=2 个宝石。杜达可以:
>
> 吃第一块石头。这需要 12 秒,并给他 300 单位的能量。 吃第二块石头。这需要 5 秒,并给他 200
> 单位的能量(第二块石头随着时间的推移不会失去任何能量!)。 所以答案是 500 。
思路:
dp+贪心
参考贪心问题:耍杂技的牛,贪心类型一样
我们要证明我们有一种吃法一定最优
从最优的吃法里开始dp而不是枚举所有的吃法然后dp

代码:
为了便于理解,先看二维dp:
#include<bits/stdc++.h>
using namespace std;
const int n=103;
const int s=10005;
int n;
struct node
{
int s,e,l;
};
node a[n];
int f[n][s];//前i个物品,总时间不超过j所获取的最大能量
bool cmp(node a,node b)
{
return a.s*b.l < b.s*a.l;
}
int main()
{
int t;
cin>>t;
int cnt=0;
while(t--)
{
memset(f, -0x3f, sizeof f);//恰好的条件:全部初始化为负无穷
int time=0;
cin>>n;
for(int i=1;i<=n;i++)
{
int s,e,l;
cin>>s>>e>>l;
time+=s;
a[i]={s,e,l};
}//读入数据,算出总时间time
sort(a+1,a+n+1,cmp);//检查半天的原因:这里的a+n+1忘记+1了!!!!!!!!!!
//真是气死人
//选前i个,总时间为0的方案数状态都是0
//for(int i=1;i<=n;i++)f[i][0]=0;
f[0][0]=0;
//开始使用背包
for(int i=1;i<=n;i++)
{
for(int j=0;j<=time;j++)
{
f[i][j]=f[i-1][j];//不选第i个
if(j>=a[i].s)f[i][j]=max(f[i][j],f[i-1][j-a[i].s]+max(0,a[i].e-a[i].l*(j-a[i].s)));//加上的是流失后的能量
//因为是恰好的情况 所以说j-a[i]就是吃前面石头消耗的能量
}
}
int res=0;
for(int i=1;i<=time;i++)res=max(f[n][i],res);//前n个物品中选择每种状态中最大的
printf("case #%d: %d\n",++cnt,res);
}
return 0;
}
优化为一维01背包:
#include<bits/stdc++.h>
using namespace std;
const int n=103;
const int s=10005;
int n;
struct node
{
int s,e,l;
};
node a[n];
int f[n][s];//前i个物品,总时间不超过j所获取的最大能量
bool cmp(node a,node b)
{
return a.s*b.l < b.s*a.l;
}
int main()
{
int t;
cin>>t;
int cnt=0;
while(t--)
{
memset(f, -0x3f, sizeof f);//恰好的条件:全部初始化为负无穷
int time=0;
cin>>n;
for(int i=1;i<=n;i++)
{
int s,e,l;
cin>>s>>e>>l;
time+=s;
a[i]={s,e,l};
}//读入数据,算出总时间time
sort(a+1,a+n+1,cmp);//检查半天的原因:这里的a+n+1忘记+1了!!!!!!!!!!
//真是气死人
//选前i个,总时间为0的方案数状态都是0
//for(int i=1;i<=n;i++)f[i][0]=0;
f[0][0]=0;
//开始使用背包
for(int i=1;i<=n;i++)
{
for(int j=0;j<=time;j++)
{
f[i][j]=f[i-1][j];//不选第i个
if(j>=a[i].s)f[i][j]=max(f[i][j],f[i-1][j-a[i].s]+max(0,a[i].e-a[i].l*(j-a[i].s)));//加上的是流失后的能量
//因为是恰好的情况 所以说j-a[i]就是吃前面石头消耗的能量
}
}
int res=0;
for(int i=1;i<=time;i++)res=max(f[n][i],res);//前n个物品中选择每种状态中最大的
printf("case #%d: %d\n",++cnt,res);
}
return 0;
}
4、金明的预算方案
思路:
这里采用了状态压缩dp,可以用一个数字表示所有的选取状态
//附件有n个就有2的n次方种状态:
i表示选前i个主件
u枚举体积
j储存了当前主件和附件的选择状态(二进制状态压缩)
k用来计算当前状态的价值
代码:
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
#define v first
#define w second
const int m=32001;//容量最大为32000
const int n=63;//最多有n种物品
pii master[n];//存储主件的pii数组
vector<pii>sec[n];//存储附件的数组
//dp
int f[m];
int n,m;
int main()
{
cin>>m>>n;
for(int i=1;i<=n;i++)
{
int v,p,q;
cin>>v>>p>>q;
p*=v;
if(!q)master[i]={v,p};//是主件的情况
else sec[q].push_back({v,p});
}
//dymanic programming
for(int i=1;i<=n;i++)
{
for(int u=m;u>=0;u--)
{
for(int j=0;j<1<<sec[i].size();j++)//附件有几个决定有几种状态
{
//附件有n个就有2的n次方种状态
//j储存了当前附件的选择状态(二进制压缩)
int v=master[i].v;
int w=master[i].w;
for(int k=0;k<sec[i].size();k++)//第k个选不选的情况
{
if(j>>k&1)//如果现在这种状态选了第k个
{
v+=sec[i][k].v;
w+=sec[i][k].w;//加上对应的价值
}
}
if(u>=v)f[u]=max(f[u],f[u-v]+w);
}
}
}
cout<<f[m]<<endl;
return 0;
}




发表评论