电子技术——电流镜负载的差分放大器_网络协议

电子技术——电流镜负载的差分放大器

logo

目前我们学习的差分放大器都是使用的是差分输出的方式，即在两个漏极之间获取电压。差分输出主要有以下优势：

降低了共模信号的增益，提高了共模抑制比。
降低了输入偏移电压。
提升了差分输入的增益。

由于差分输出巨大的优势使得几乎大部分集成ic放大器的初级输入都使用了 差分输入，差分输出 的模式，例如运算放大器。这使得集成ic放大器拥有优越的信号抗干扰能力，特别是针对于共模信号。尽管如此，有时我们不得不使用单端输出的方式，例如片外负载。下图展示了一个运算放大器基本原理图：

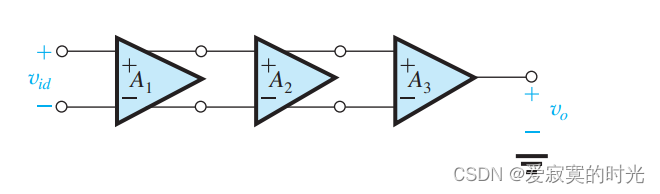
这个运算放大器前两级都是使用的差分输入，差分输出，最后一级将差分输出转换为单端输出。我们现在就来解决差分输出转换为单端输出的问题。

差分到单端输出

下图展示了一个最简单的差分到单端输出的方案：

单端输出
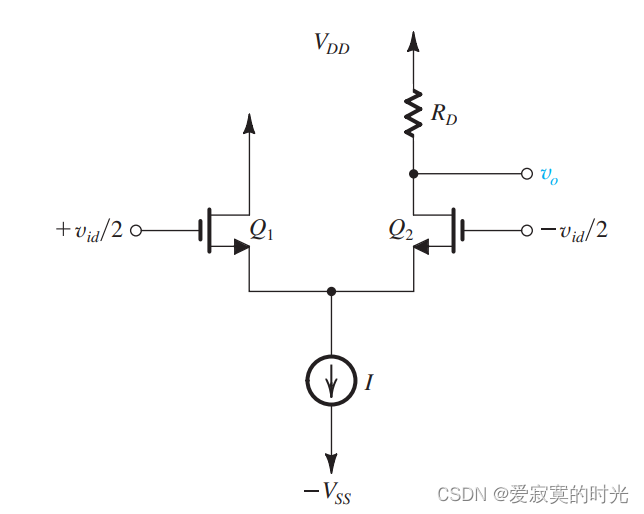
仅仅用一个输出端作为输出，因此 $q_1$ 的负载电阻是可以省略的。但是这个电路有一个缺点，就是损失了一半的电压增益，而且还浪费了 $q_1$ 的电流。一个更好的方法是将 $q_1$ 的电流利用起来，这就是我们要讨论的。

电流镜负载的mos差分放大器

下图展示了一个mos差分放大器，只不过负载变成了一个电流镜：

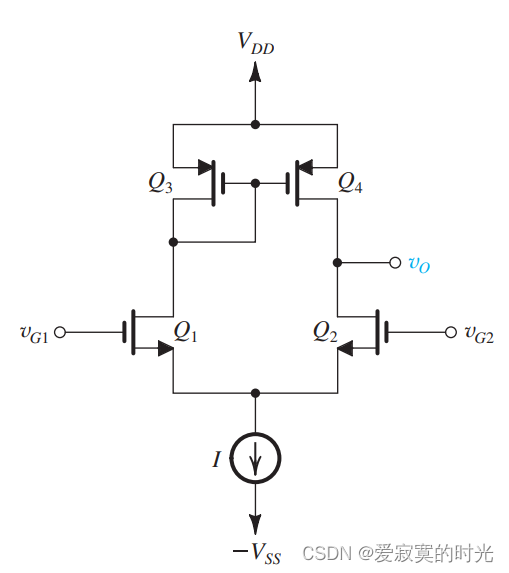
电流镜负载的mos差分放大器

为了说明该电路的工作方式，我们先讨论平衡的情况，也就是令 $v_{g1} = v_{g2} = 0$ 如图：

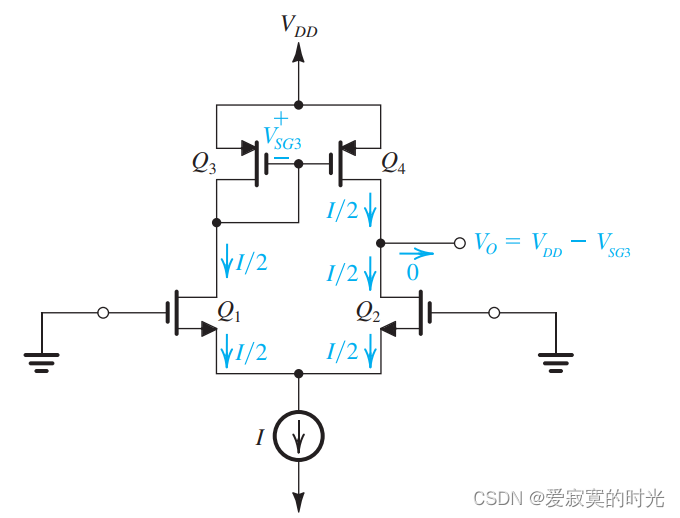
平衡的情况
因为电路的对称的，因此mos $q_1$ 和 $q_2$ 的漏极电流相等且都为 $i /2$ ，其中 $q_1$ 的电流流向电流镜的电流采集输入 $q_3$ ，这将在 $q_4$ 复制出电流 $i /2$ 。观察输出节点，我们发现从 $q_4$ 流入和从 $q_2$ 流出的电流均为 $i /2$ ，也就是说输出电流为零，这正是我们想要的结果。而且，假设 $q_3$ 和 $q_4$ 完全匹配，此时的输出电压应为 $v_o = v_{dd} - v_{sg3}$ 。值得注意的是，实际情况下电路总是不对称的，因此存在净电流从输出端流出，在缺少负载电阻的情况下，净电流通过 $q_4$ 和 $q_2$ 的输出阻抗，这将造成输出电压与理论值存在较大的偏差。因此这个电路的偏置通常被负反馈所控制，之后我们会学习到。

接下来考虑应用一个差分信号 $v_{id}$ ，如图：

差分信号

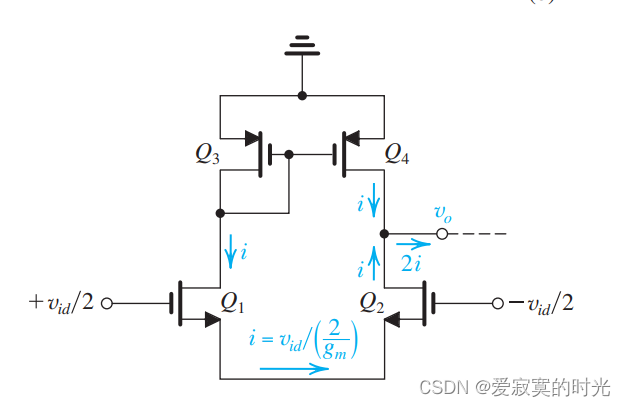
因为我们讨论的是小信号，所有我们移除了所有的dc分量。根据我们之前的分析， $q_1$ 和 $q_2$ 的源极电流仍为：

$v_{id} /(\frac{2}{g_m})$

各个支路的电流方向如图所示，我们发现，流出输出节点的电流变成了 $2 i$ ，我们无损的做到了将差分输出转为了单端输出。我们这里省略了输出负载，实际上的输出电压由 $2_i$ 和输出负载共同决定。

实际上，这个电路的精髓就在于：当输入的是共模信号的时候， $q_4$ 输出的电流被 $q_2$ 抵消。当输入的是差分信号的时候，此时 $q_4$ 输出的电流被 $q_2$ 叠加。

电流镜负载的差分放大器的差分增益

我们知道在ic中， $r_o$ 的作用无法忽视。因此我们将在考虑 $r_o$ 的情况下计算 $v_o / v_{id}$ 的值。我们发现，若考虑 $r_o$ ，那么电路本身是不对称的，因为 $q_1$ 看向 $q_3$ 的阻抗较小，大约为 $1/g_{m3}$ ，而 $q_2$ 看向 $q_4$ 的阻抗是较大的，大约为 $r_{o4}$ ，此时共源极端点不再是虚拟地，因此我们不能使用半电路分析法。

我们的分析方法是，将电路等效为一般形式：

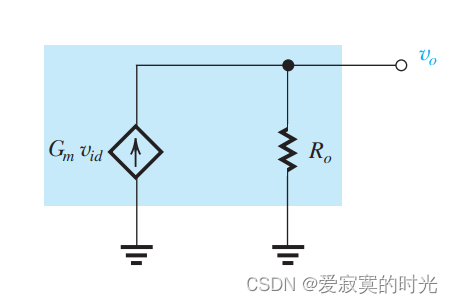
这里 $g_m v_{id}$ 是电流镜负载的差分放大器的输出信号电压， $r_o$ 是输出阻抗。我们先给出结论：

这里 $g_m$ 是整体传导系数，其值为：

$g_m = g_{m1,2}$

这里 $g_{m1,2}$ 是 $q_1$ 和 $q_2$ 的互导系数。

$r_o = r_{o2} || r_{o4}$

此时开路电压增益为：

$a_d \equiv \frac{v_o}{v_{id}} = g_mr_o = g_{m1,2}(r_{o2} || r_{o4})$

我们将 $g_{m1,2}$ 简记为 $g_m$ ，并且令 $r_{o2} = r_{o4} = r_o$ ，则：

$a_d = \frac{1}{2}g_m r_o = \frac{1}{2}a_0$

这里 $a_0$ 是固有增益。

首先我们推导短路互导系数，下图中，我们将输出端置地：

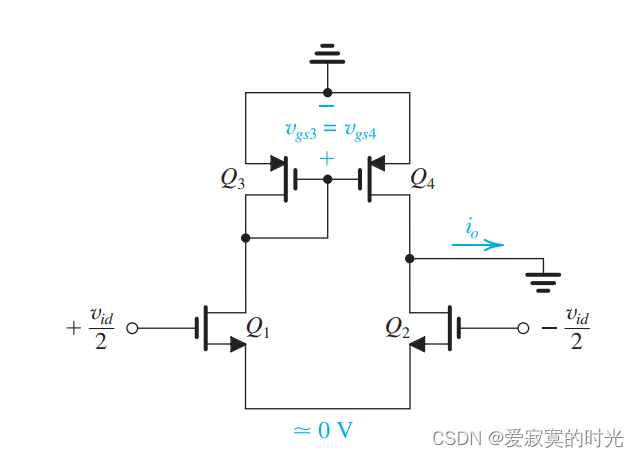
输出端置地
则短路互导系数定义为：

$g_m \equiv \frac{i_o}{v_{id}}$

观察到将输出端置地后，此时的电路几乎是平衡状态，因为从 $q_1$ 看向 $q_3$ 是一个接近零的小阻抗，从 $q_2$ 看向 $q_4$ 此时阻抗为零。因此我们近似的将共源极端点的电压看做是零点。紧接着我们将其使用混合 $\pi$ 模型展开，注意到 $q_3$ 可以看做是输出阻抗为 $1/g_{m3}||r_{o3}$ 的二极管：

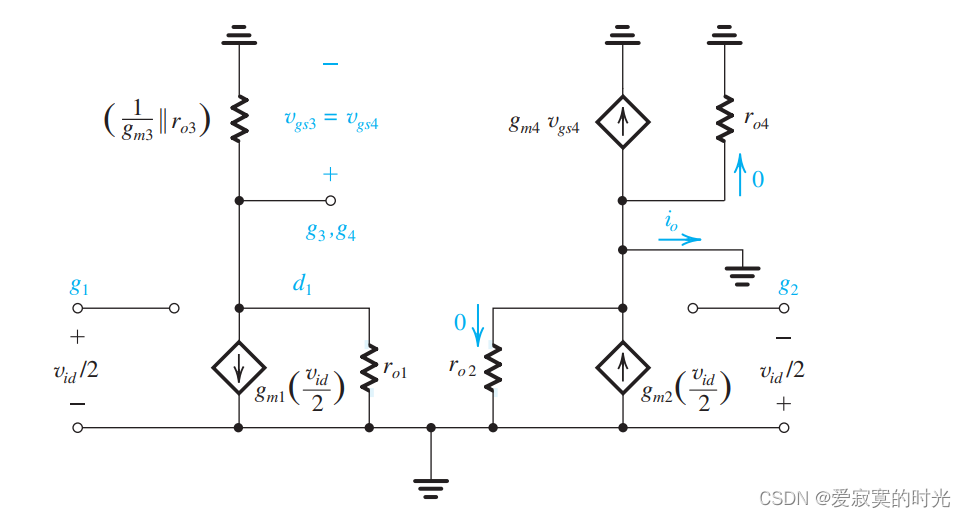
混合pi模型
通过节点电压法我们能够写出：

$i_o = g_{m2}(\frac{v_{id}}{2})-g_{m4}v_{gs4}$

注意到：

$v_{gs3} = v_{gs4}$

而且：

$v_{gs3} = -g_{m1}(\frac{v_{id}}{2})(\frac{1}{g_{m3}}||r_{o3}||r_{o1})$

因为 $\frac{1}{g_{m3}} \ll r_{o3},r_{o1}$ 所以：

$v_{gs3} \simeq -\frac{g_{m1}}{g_{m3}}(\frac{v_{id}}{2})$

若此时 $g_{m3} = g_{m4}$ 并且 $g_{m1} = g_{m2} = g_m$ 则：

$i_o = g_m v_{id}$

则：

$g_m = g_m$

最后我们推导输出阻抗 $r_o$ ，下图中我们将输入端置地，在输出端接入测试电压源：

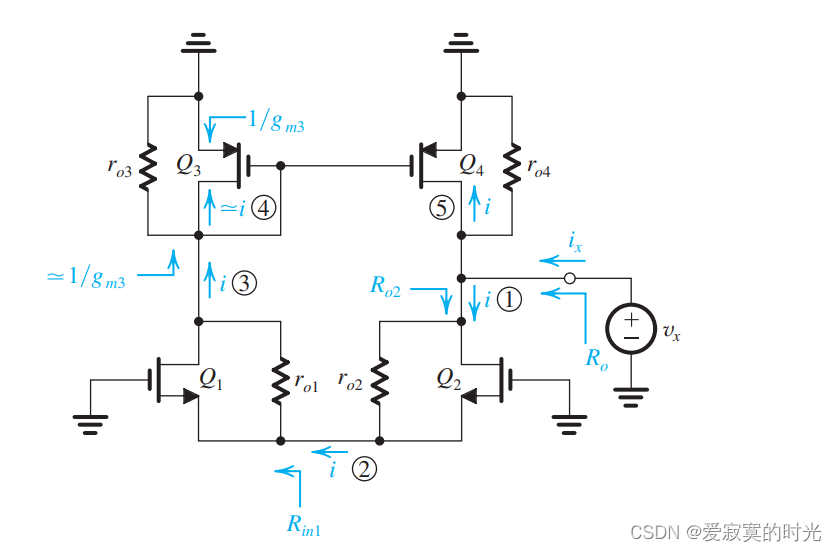
测试电压源
则输出阻抗定义为：

$r_o \equiv \frac{v_x}{i_x}$

在图中，我们将分析顺序使用编号标出，电流 $i$ 依次流入 $q_2$ $q_1$ ，因为 $q_3$ 是二极管接法，而且 $1/g_{m3} \ll r_{o3}$ 所以大部分电流都流入 $q_3$ ，这将导致在 $q_4$ 也复制出相同的电流 $i$ 。根据输出端点电压：

$i = i_x / r_{o2}$

这里 $r_{o2}$ 是从输出端点向下看的阻抗。为了计算 $r_{o2}$ 我们先计算电流镜 $q_3$ 的输入阻抗：

$r_{in3} = \frac{1}{g_{m3}}||r_{o3} \simeq \frac{1}{g_{m3}}$

然后是cg放大器 $q_1$ 的输入阻抗，在上一章我们计算过为：

$r_{in1} = \frac{r_{o1} + r_l}{g_{m1}r_{o1}}$

带入 $r_l = r_{in3} = \frac{1}{g_{m3}}$ ：

$r_{in1} = \frac{1}{g_{m1}} + \frac{1/g_{m3}}{g_{m1}r_{o1}} \simeq \frac{1}{g_{m1}}$

此时 $r_{o2}$ 是cg放大器 $q_2$ 的输出阻抗，在上一章我们计算过为：

$r_{o2} = r_{in1} + r_{o2} + g_{m2}r_{o2}r_{in1} = \frac{1}{g_m1} + r_{o2} + \frac{g_{m2}}{g_{m1}}r_{o2}$

这里令 $g_{m1} = g_{m2} = g_m$ 则：

$r_{o2} \simeq 2r_{o2}$

带回原方程我们得到：

$i_x = i + i + \frac{v_x}{r_{o4}} = 2 \frac{v_x}{r_{o2}} + \frac{v_x}{r_{o4}} = \frac{v_x}{r_{o2}} + \frac{v_x}{r_{o4}}$

所以：

$r_o = r_{o2} || r_{o4}$

电流镜负载的bjt差分放大器

bjt版本的电流镜负载的bjt差分放大器如下图所示：

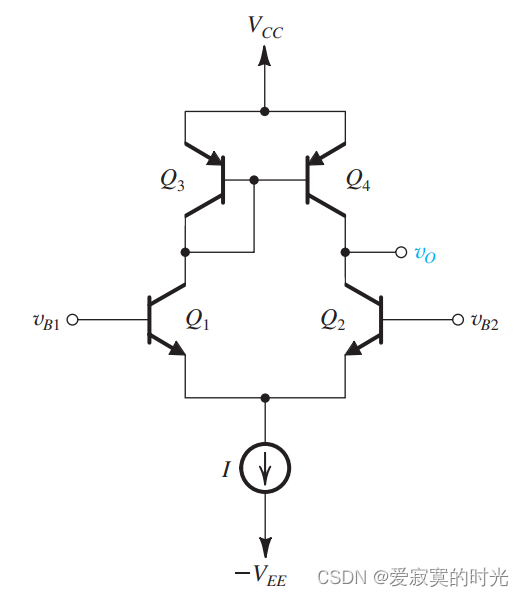
电流镜负载的bjt差分放大器
在这里我们忽略有限 $\beta$ 的基极电流的影响，并且假设电路是平衡的，我们分析的方法和mos一样。其中短路互导系数为：

$g_m = g_{m1,2}$

输出阻抗为：

$r_o = r_{o2} || r_{o4}$

与mos一致。

开路差分增益为：

$a_d = \frac{v_o}{v_{id}} = g_mr_o = g_m(r_{o2} || r_{o4})$

这里若 $g_{m1} =g_{m2} =g_m = \frac{v_t}{i/2}$ 以及 $r_{o2} = r_{o4} = r_o$ ，则：

$a_d = \frac{1}{2} g_m r_o$

以上均和mos的情况一致，但是bjt的 $g_m$ 要比mos的大很多因此增益要比mos大，但是因为基极电流的影响，其存在有限的输入阻抗：

$r_{id} = 2 r_\pi$

系统性输入偏移电压误差

考虑到bjt电流镜即使完全匹配，其电流传导比也不是单位一。因此在bjt电流镜中存在系统误差，如图：

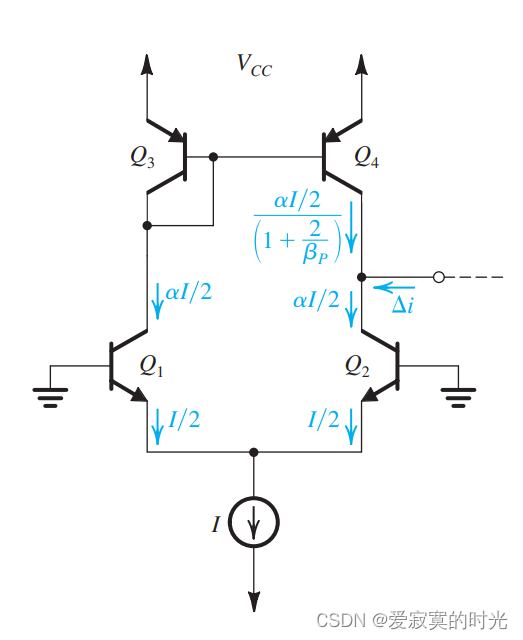
系统性输入偏移电压误差
此时 $q_4$ 输出的电流为：

$i_4 = \frac{\alpha i/2}{1 + \frac{2}{\beta_p}}$

与 $q_2$ 的输出电流不匹配，因此输出端存在净电流：

$\delta i = \frac{\alpha i}{2} - \frac{\alpha i/2}{1 + \frac{2}{\beta_p}} \simeq \frac{\alpha i}{\beta_p}$

为了让误差归零，我们必须额外的输入差分电压：

$v_{os} = -\frac{\delta i}{g_m} = -\frac{2v_t}{\beta_p}$

一个改进的方法是使用高级电流镜。

共模增益和共模抑制

电路在任何时候都不是理想情况，因此电流镜负载的差分放大器也存在共模增益和共模抑制。因为电流镜的传导比实际上是一个非常接近于单位一的数字，当输入一个共模信号，和 $q_2$ 的抵消电流就会出现不相等的情况，因此存在一个共模信号输出。我们希望推导出 $a_{cm}$ 。下图是我们使用的电路图：

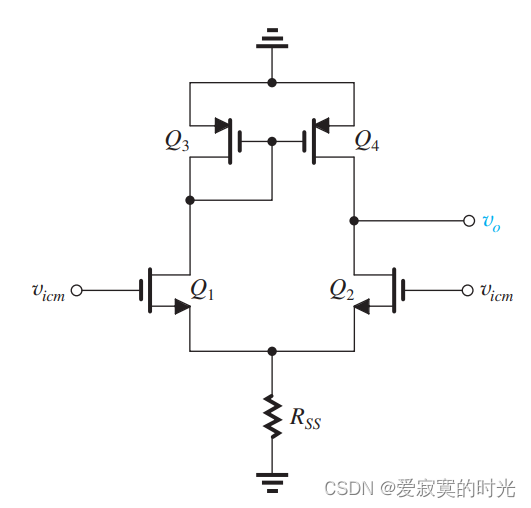
共模增益和共模抑制
注意到我们省去了dc偏移，并且只留下了 $r_{ss}$ 。尽管负载电路是不对称的，但是这不影响我们可以将 $r_{ss}$ 拆开为：

等效电路
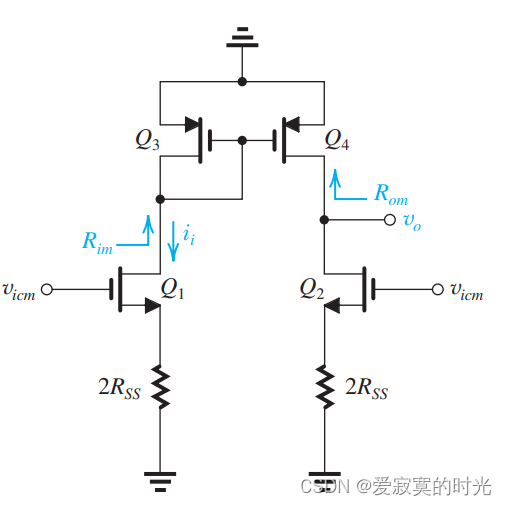
这相当于带源极电阻 $2r_{ss}$ 的cs放大器。其等效模型为：

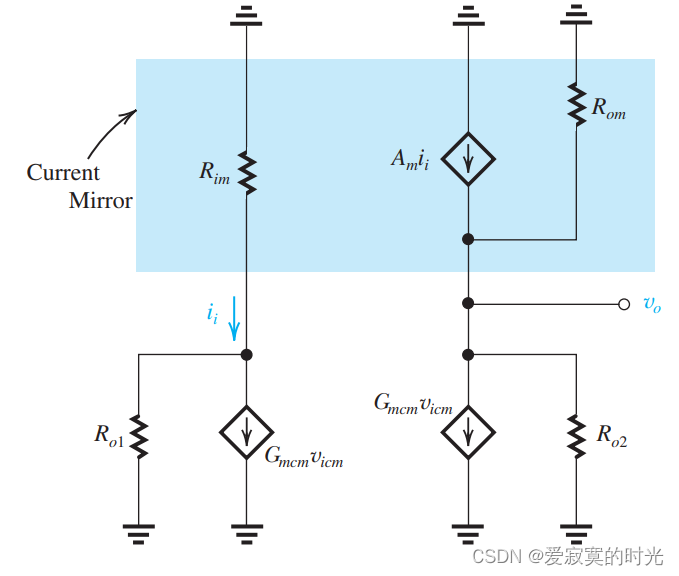
混合pi模型
为了决定 $g_{mcm}$ 的大小，我们将 $q_1$ 的漏极置地得到：

漏极置地
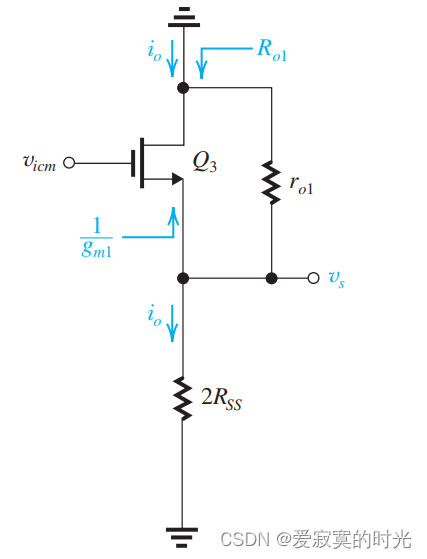
在上图中：

$v_s = v_{icm} \frac{(2r_{ss}||r_{o1})}{(2r_{ss}||r_{o1}) + (1/g_{m1})} \simeq v_{icm}$

则 $i_o$ 为：

$i_o = \frac{v_c}{2r_{ss}} \simeq \frac{v_{icm}}{2r_{ss}}$

所以互导系数为：

$g_{mcm} \equiv \frac{i_o}{v_{icm}} = \frac{1}{2r_{ss}}$

$r_o$ 是带源极电阻的cs放大器的输出阻抗为：

$r_{o1} = 2r_{ss} + r_{o1} + (g_{m1}r_{o1})(2r_{ss})$

同样的：

$r_{o2} = 2r_{ss} + r_{o2} + (g_{m2}r_{o2})(2r_{ss})$

现在对于电流镜的输入阻抗为 $r_{im}$ 电流传导比为 $a_m$ 输出阻抗为 $r_{om}$ 这对于任何的电流源均适用，因为 $r_{o1}$ 要远大于 $r_{im}$ 所以电流源的输入电流为 $i_i$ ：

$i_i \simeq g_{mcm} v_{icm}$

此时输出电压为：

$v_{o} = (a_m i_i - g_{mcm}v_{icm})(r_{om} || r_{o2})$

全部带入得到：

$a_{cm} \equiv \frac{v_o}{v_{icm}} = -(1 - a_m)g_{mcm}(r_{om} || r_{o2})$

这是一个通用的公式，适用于所有的电流镜。针对于简单电流镜：

$r_{im} = \frac{1}{g_{m3}} || r_{o3}$

$r_{om} = r_{o4}$

电流增益为：

$a_m i_i = -g_{m4}v_{gs4} = -g_{m4}v_{gs3}$

这里：

$v_{gs3} = -i_i r_{in}$

因此：

$a_{m} = g_{m4}r_{in}$

假设 $g_{m4} = g_{m3}$ 有：

$a_m = 1 / (1 + \frac{1}{g_{m3} r_{o3}})$

整体带入得到：

$a_{cm} \simeq -\frac{1}{2g_{m3}r_{ss}}$

这是因为 $r_{o4} \ll r_{o2},r_{o4} = r_{o3},g_{m}r_{o3} \ll 1$ 。

因此共模抑制比为：

$\equiv \frac{|a_d|}{|a_{cm}|} = [g_m(r_{o2} || r_{o4})][2g_{m3}r_{ss}]$

对于 $r_{o2} = r_{o4} = r_o$ 并且 $g_{m3} = g_m$ 来说：

$cmrr = (g_mr_o)(g_mr_{ss})$

我们发现要提高cmrr可以提高偏置电流 $i$ 或者提供输出阻抗，这可以使用共源共栅电流镜或者高级电流镜。

bjt情况

对于bjt来说：

$g_{mcm} = \frac{1}{2r_{ee}}$

并且：

$r_{im} = \frac{1}{g_{m3}} || r_{\pi 3} || r_{\pi 4} || r_{o3}$

因为 $r_{o3} \gg r_{\pi 3}$ 并且 $r_{\pi 3} = r_{\pi 4}$ 得到：

$r_{im} \simeq \frac{1}{g_{m3}} || \frac{2}{r_{\pi 3}}$

$r_{om} = r_{o4}$

电流传导比为：

$a_{m} = g_{m4}r_{im}$

假设 $g_{m4} = g_{m3}$ 使用 $r_{o4} \gg r_{o2}$ ：

$a_{cm} \simeq -\frac{r_{o4}}{2r_{ee}}\frac{\frac{2}{r_{\pi 3}}}{g_{m3} + \frac{2}{r_{\pi 3}}} \simeq -\frac{r_{o4}}{2r_{ee}} \frac{2}{\beta_3} = -\frac{r_{o4}}{\beta_3 r_{ee}}$

则共模抑制比为：

$g_{m}(r_{o2}||r_{o4})(\frac{\beta_3r_{ee}}{r_{o4}})$

对于 $r_{o2} = r_{o4} = r_o$ 来说：

$\frac{1}{2}\beta_3 g_m r_{ee}$

同样的为了提高bjt的cmrr，我们可以使用较大的偏置电流，或者使用较高输出阻抗的高级电流镜。

总结：电流镜负载的差分放大器共模增益主要原因是由于电流镜的电流传导比上的误差，对于mos来说这是由于 $r_{o3}$ 引起的，对于bjt来说是由于有限的 $\beta$ 引起的。

电子技术——电流镜负载的差分放大器

2024年08月02日 • 网络协议 •我要评论