![实现堆排序,函数void heapadjust(sqlist &l,int s,int m)为筛选法调整堆,函数void creatheap(sqlist &l)把无序序列l.r[1..n]建成大根堆,函数void heapsort(sqlist &l)对顺序表l进行堆排序。](https://images.3wcode.com/3wcode/20240801/b_0_202408012331034933.png)
函数接口定义:
void heapadjust(sqlist &l,int s,int m);//筛选法调整堆
void creatheap(sqlist &l); //把无序序列l.r[1..n]建成大根堆
void heapsort(sqlist &l);//对顺序表l进行堆排序
裁判测试程序样例:
```cpp
#include <iostream>
#define maxsize 1000
using namespace std;
typedef struct
{
int key;
char *otherinfo;
}elemtype;
typedef struct
{
elemtype *r;
int length;
}sqlist;
void create_sq(sqlist &l)
{
int i,n;
cin>>n; //输入的值不大于 maxsize
for(i=1;i<=n;i++)
{
cin>>l.r[i].key;
l.length++;
}
}
void show(sqlist l)
{
int i;
for(i=1;i<=l.length;i++)
if(i==1)
cout<<l.r[i].key;
else
cout<<" "<<l.r[i].key;
}
void heapadjust(sqlist &l,int s,int m);//筛选法调整堆
void creatheap(sqlist &l); //把无序序列l.r[1..n]建成大根堆
void heapsort(sqlist &l);//对顺序表l进行堆排序
int main()
{
sqlist l;
l.r=new elemtype[maxsize+1];
l.length=0;
create_sq(l);
heapsort(l);
show(l);
return 0;
}
/* 请在这里填写答案 */
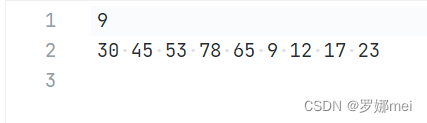
输入样例:
9
30 45 53 78 65 9 12 17 23
输出样例:
9 12 17 23 30 45 53 65 78
代码如下
// 堆化,保持堆的性质
// 从元素l.r[i].key,l.r[lt].key,l.r[rt].key中找出最大的,并将其下标保存在largest中。
// 如果l.r[i].key是最大的,则以i为根的子树成已为最大堆,程序结束。
// 否则,i的某个子节点中有最大元素,则交换l.r[i].key,l.r[largest].key从而使i及其子女满足堆性质。
// 下标为largest的结点在交换后的值为l.r[i].key,以该结点为根的子树又有可能违反最大堆性质。因而要对该子树递归调用heapadjust。
void heapadjust(sqlist &l, int i, int size)
{
int lt = 2*i, rt = 2*i+1;
int largest;
if(lt <= size && l.r[lt].key > l.r[i].key) //右孩子没有超过结点总数,且右孩子大于根节点。
largest = lt; //便把右孩子的下标记下来,给最大值下标
else
largest = i; //否则把根节点的下标记下来,给最大值下标
if(rt <= size && l.r[rt].key > l.r[largest].key) /*再和左孩子的值进行比较。左孩子没有超过结点总数,且左孩子大于最大结点的值*/
largest = rt; //将左孩子下标记下来,给最大值下标
if(largest != i) //如果最大值下标不是根节点,则进行key值的交换
{
int temp = l.r[i].key;
l.r[i].key = l.r[largest].key;
l.r[largest].key = temp;
heapadjust(l, largest, size); //继续调用heapadjust函数,进行最大堆的排序。
}
}
// 建堆
/*自底而上地调用heapadjust来将一个数组a[1..size]变成一个最大堆.一定要自下而上的调用,
才能保证调用较小层次的结点的堆排序算法时,较高层次以及满足堆的性质。否则可能导致中间层次出现最大值。*/
// 注意: [size/2]以后的结点为叶子结点,即已经满足堆的性质
void creatheap(sqlist &l)
{
for(int i=l.length/2; i>=1; --i) //当为满二叉树时,分支节点数n2,总结点数n=2n2+1,叶子节点数=n/2+1=n2+1
heapadjust(l, i, l.length);
}
// 堆排序
// 初始调用creatheap将l.r[1..size].key变成最大堆
// 因为数组最大元素在l.r[1].key,则可以通过将l.r[1].key与l.r[size].key互换达到正确位置
// 现在新的根元素破坏了最大堆的性质,所以调用heapadjust调整,
// 使l.r[1..size-1].key成为最大堆,l.r[1].key又是l.r[1..size-1].key中的最大元素,
// 将l.r[1].key与l.r[size-1].key互换达到正确位置。
// 反复调用heapadjust,使整个数组成从小到大排序。
// 注意: 交换只是破坏了以l.r[1].key为根的二叉树最大堆性质,它的左右子二叉树还是具备最大堆性质。
// 这也是为何在creatheap时需要遍历size/2到1的结点才能构成最大堆,而这里只需要堆化l.r[1].key即可。
void heapsort(sqlist &l)
{
creatheap(l );
int len = l.length;
for(int i=l.length; i>=2; --i)
{
int temp = l.r[1].key;
l.r[1].key = l.r[i].key;
l.r[i].key = temp; /*因为最大堆只能保证第一个元素l.r[1].key是最大值,不能保证最后一个元素是最小值*/
len--; /*所以只能通过每次把最大值,也就是l.r[1].key放在数组末尾,才能得到从小到大的序列*/
heapadjust(l, 1, len); /*不包括已排好序的l.r[len]后面的数组元素,在未排好序的部分做最大堆的算法*/
}
}








发表评论