目录
创建二叉树
实现思路
想要创建二叉树,首先就要有一个理论基础。
二叉树(binary tree)可以理解为子节点最多为2的树,也就是说每个节点(node)的度(degree)都不大于2。什么是度呢?度指的是一个节点拥有子树的数目。如下图,a点的度为2,因为它有两个节点b,c,同时,a也被称为根节点,因为该节点上面再没有点了。另外,我们可以看到,这棵二叉树有4层节点,换句话说,该树的深度为4。
那节点包含什么呢?节点包含了数据项以及指向子树节点的指针。我们应该注意到了h,i,l等在最后一层的节点,它们没有子节点。像这种度为0的节点,我们称之为叶节点(leaf)。
二叉树没有规定每个节点的度必须是二,于是这里就衍生出了几种二叉树。
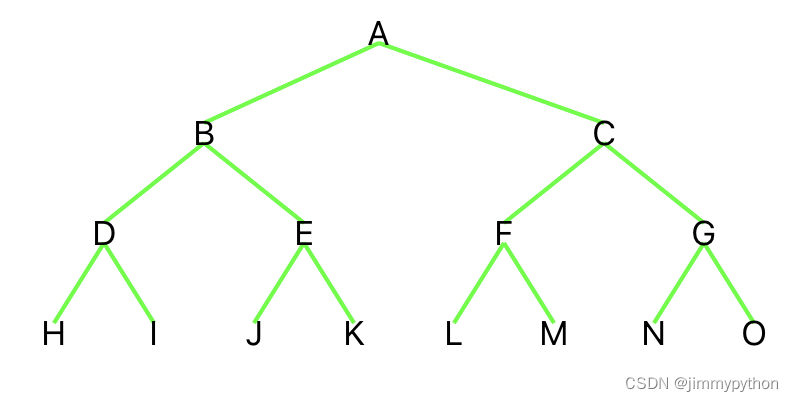
第一种是满二叉树。如上图所示,满二叉树指的是度只有0或2的树,而且度为0的节点在同一层内。其实就是除了最后一层没有任何子节点外,每一层的节点都有两个子节点。那这满二叉树的总节点又是多少呢?让我们观察一下。深度为2的满二叉树总节点为3;深度为3的总节点是7;深度为4的总节点是15……想必大家都已经发现规律了,对于一个深度为h的满二叉树,其总节点数=2^h-1。由此我们也不难推出,满二叉树中每一层的节点数=2^(h-1)。
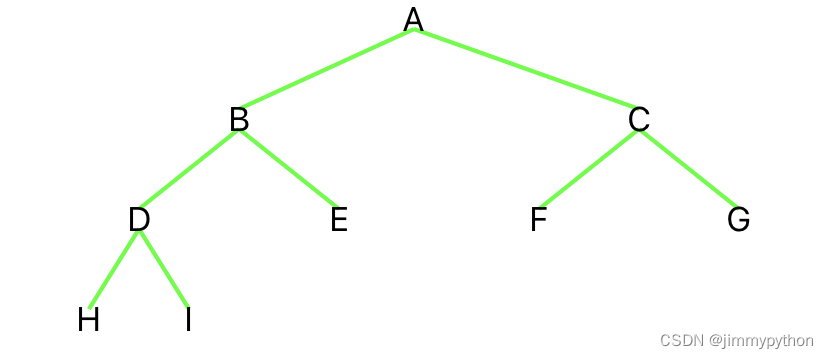
第二种是完全二叉树。上图(图2)就是一个完全二叉树。完全二叉树由满二叉树衍生而来。若一个二叉树有h层,从1~h-1层的所有节点数都达到最大个数,且第 h 层所有的结点都连续集中在最左边,就是完全二叉树。比如回到图1,我们砍掉o点后它就变成了个完全二叉树。什么?还想砍?我们需要按照这个顺序砍:o->n->m……如果你砍完o后就心急火燎的把m砍掉了,这就不是一个完全二叉树了,因为m比n更靠左,要先砍n才能砍m。




发表评论