目录
本期我们将探讨动态规划,并提供5道经典动态规划问题,难度由浅入深。
一、什么是动态规划
1、什么是动态规划
在学习算法的过程中,我们往往会遇到一些算法题是要用动态规划来解决。
但是做为小白的我们哪里知道动态规划是什么?
从概念上说

看完概念我们知道什么是动态规划,求重叠类子问题的 一般会用到动态规划的思路。
那我们如何求学习动态规划
2、动态规划的学习
对于算法类题目,在我们掌握算法的基本原理后,就是进行大量刷题,进经验的总结。
求解动态规划的五步骤:
1、状态表示
在求解过程中,我们往往要创建dp表(其实就是数组),状态表示就是我们要找出dp表中值的含义是什么。
状态表 怎么来?
2、状态转移方程
3、初始化
4、填写顺序
5、返回值
讲完了解题步骤,下面就进行刷题训练。
特别提醒:后面博客会带领大家由易到难进行刷题,每期都为五题。
二、动态规划刷题
1、第 n 个泰波那契数
a、解题思路:
1、题目中的状态表示是什么?
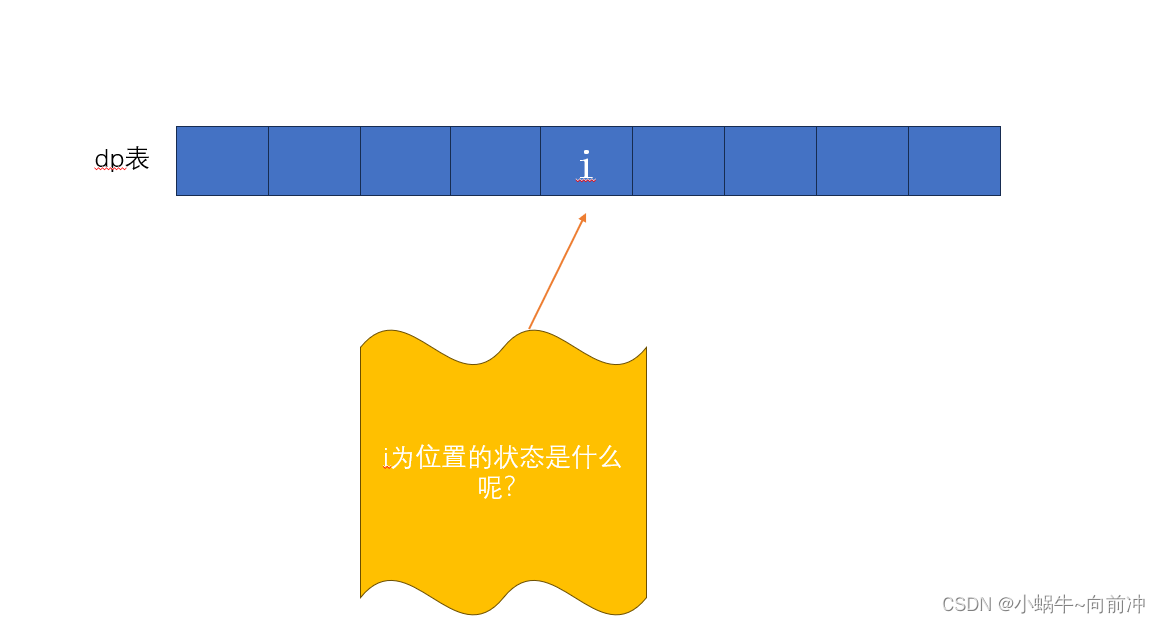
dp[i] 表⽰:第 i 个泰波那契数的值。
2、状态转移方程
由题目意很很容易知道是t(n) = t(n-1)+t(n-2)+t(n-3)
3、初始化dp表
为了防止数组越界我们只需要初始化:
4、 填表顺序
由状态方程+题意知道从左往右填写到n
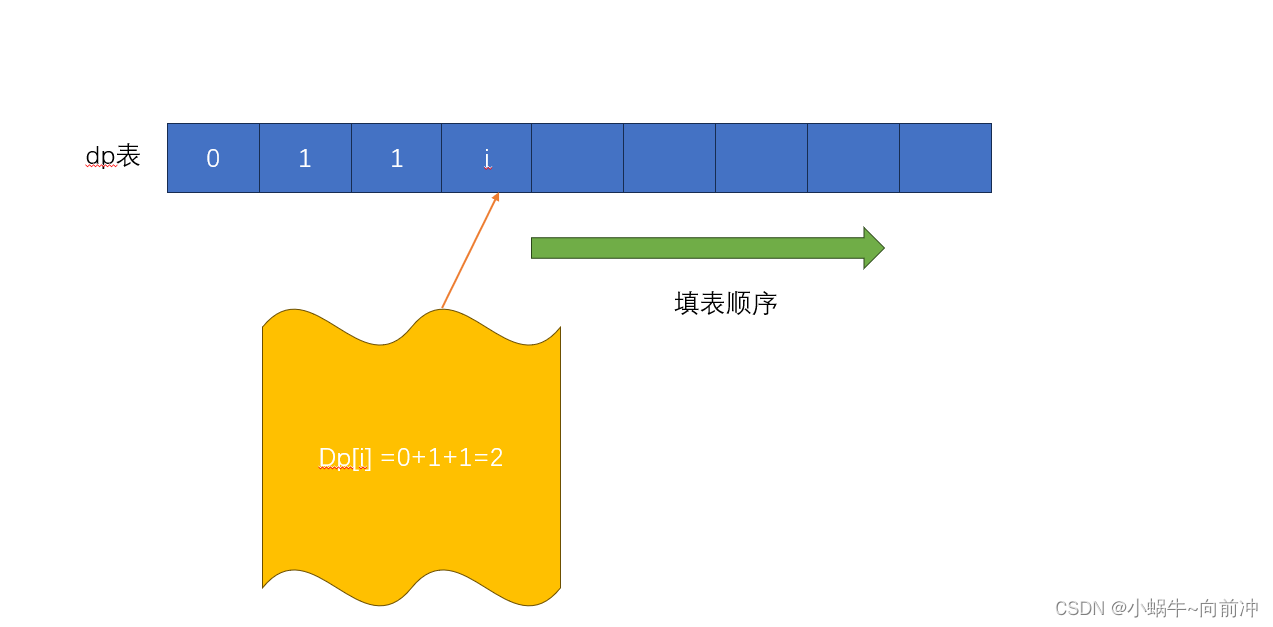
5、返回值
根据题目要求和dp[i]就为dp[n]
b、代码
class solution {
public:
int tribonacci(int n)
{
//动态规划
//1.创建dp表
//2.初始化表
//3.填表
//4.返回值
//处理边界情况
if(n==0)return 0;
if(n==1||n==2)return 1;
//1、创建dp表
vector<int> dp(n+1);
//2、初始化表
dp[0]=0,dp[1]=1,dp[2]=1;
//3、填表
for(int i = 3;i<=n;i++)
{
dp[i] = dp[i-1]+dp[i-2]+dp[i-3];
}
//4、返回
return dp[n];
}
};leetcode 测试结果:
2、 面试题 08.01. 三步问题
a、解题思路:
从0位置开始跳,下面我们来思考一下题意:
----->(表示跳台阶)
大家这里是不是已经思路清晰起来了
1、转态表示
以i位置为结尾,正好是到达第n个台阶,所以我们认为:
dp[i]表示:到达i位置时,一共有多少方法。

2、状态转移方程
以i位置的状态,最近进的一步进行划分
所以状态方程为:dp[i]=dp[i-1]+dp[i-2]+dp[i-3] ;
3、初始化
这里我们注意我们用不到i==0,因为0台阶的研究没有意义。
dp[1] = 1, dp[2] = 2, dp[3] = 4;
4、 填表顺序
根据前面的推断肯定是从左往右。
5、返回值
根据题目要求和dp[i]就为dp[n]
b、代码
这题虽然和第一题非常相似但是有细节要处理、
class solution {
public:
//取模
const int mod = 1e9 + 7;
int waystostep(int n)
{
//处理边界情况:
if (n == 1 || n == 2)return n;
if (n == 3)return 4;
//创建dp表
vector<int> dp(n + 1);
//初始化
dp[1] = 1, dp[2] = 2, dp[3] = 4;
//填表
for (int i = 4; i <= n; i++)
{
//结果可能很大要进去取模
dp[i] = ((dp[i - 1] + dp[i - 2]) % mod + dp[i - 3]) % mod;
}
//返回
return dp[n];
}
};leetcode 测试结果: 
3 、746. 使用最小花费爬楼梯
a、解题思路
这里我们要注意到达楼顶,应该是const数组最后一个位置的下一个位置
这里我们有二种思路:
思路一:
1、转态表示
以i位置为结尾,正好是楼顶,所以我们认为:
dp[i]表示:到达i位置时,最小花费
2、状态转移方程
根据最近的一个位置划分
所以dp[i] =min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
3、初始化
保证dp表不越界就好dp[0]=dp[1]=0;
4、 填表顺序
从左往右
5、返回值
dp[n]
思路2:
1、转态表示
以i位置为起点,到达楼顶,所以我们认为:
dp[i]表示:从i位置出发到达楼顶,此时最小花费
2、状态转移方程
根据最近的一个位置划分
所以dp[i] =min(dp[i+1]+cost[i],dp[i+2]+cost[i]);
3、初始化
保证dp表不越界就好dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];
4、 填表顺序
从右往左
5、返回值
min(dp[0],dp[1]);
b、代码
这里有二种解题思路:
思路一:
class solution {
public:
int mincostclimbingstairs(vector<int>& cost)
{
//处理边界情况
int n = cost.size();
if(n==0||n==1)return cost[n];
//创建dp表
vector<int> dp(n+1);
//填表
for(int i = 2;i<=n;i++)
{
dp[i] =min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
//返回
return dp[n];
}
}; leetcode 测试结果: 
解法二:
class solution {
public:
int mincostclimbingstairs(vector<int>& cost)
{
int n = cost.size();
//创建dp表
vector<int> dp(n+1);
//初始化
dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];
//填表
for(int i = n-3;i>=0;i--)
{
dp[i] = min(dp[i+1]+cost[i],dp[i+2]+cost[i]);
}
//返回
return min(dp[0],dp[1]);
}
};leetcode 测试结果:
4、解码方法
a、解题思路
看我们题目后,根据经验此题位动态规划解题
1、转态表示
首先我们想以i位置为结尾表示什么
dp[i]表示:以i位置结尾的时候,解码的方法有多少种
2、状态转移方程
根据最近的一个位置划分
让s[i]单独解码的时候,假设a=s[i]
让s[i-1]和s[i]组合进行解码 假设组合为b
有同学可能会想为什么不让dp[i]和dp[i+1]进行组合,但是大家 要明白,填表到dp[i]的时候,我们是知道dp[i-1]有多少种解码,但是我们不知道dp[i+1]有多少种解码。
所以状态转移方法为
3、初始化
保证dp表
dp[0] = s[0]!='0';
if(s[0]!='0'&&s[1]!='0') dp[1] +=dp[0];
//这里我们还要把组合转换为数字进行判断
int t = (s[0]-'0')*10+(s[1]-'0');
if(t>=10&&t<=26) dp[1] +=1;4、 填表顺序
从左往右
5、返回值
dp[n-1]
b、代码
class solution {
public:
int numdecodings(string s)
{
//创建dp表
int n = s.size();
vector<int> dp(n);
//初始化
dp[0] = s[0]!='0';
//处理边界情况
if(n==1) return dp[0];
//单解码
if(s[0]!='0'&&s[1]!='0') dp[1] +=dp[0];
//组合起来
int t = (s[0]-'0')*10+(s[1]-'0');
if(t>=10&&t<=26) dp[1] +=1;
//填表
for(int i = 2;i<n;i++)
{
//单解码
if(s[i]!='0') dp[i] +=dp[i-1];
//双解码
int t = (s[i-1]-'0')*10+(s[i]-'0');
if(t>=10&&t<=26) dp[i] +=dp[i-2];
}
//返回
return dp[n-1];
}
};leetcode 测试结果:
c、代码优化
不知道大家分发现没,我们在初始化的代码和填表的代码,有着非常相似的特色,那我们能不能进行优化呢?
其实是可以的,多一个数组的空间就可以了。

简单的理解就是,把初始化的过程和填表合并了。但要注意二个问题:
那个虚拟节点dp[0]填写多少?后面大家做都了这种题,很多情况下都是填写0但,但是这里却是填写dp[0]=1;
为什么了,因为我们这里要保证后面填写的正确
比如:在进双解码的时候dp[i]+=dp[i-2],如何i=2时候,这里我们吧dp[0]初始化为0就会漏掉这种情况。
下标映射关系如上图。
class solution {
public:
int numdecodings(string s)
{
//创建dp表
int n = s.size();
vector<int> dp(n+1);
//初始化
dp[0] = 1;//保证后面的填表的正确性
//处理边界情况
dp[1] = s[1-1]!='0';
if(n==1) return dp[1];
//填表
for(int i = 2;i<=n;i++)
{
//单解码
if(s[i-1]!='0') dp[i] +=dp[i-1];
//双解码
int t = (s[i-2]-'0')*10+(s[i-1]-'0');
if(t>=10&&t<=26) dp[i] +=dp[i-2];
}
//返回
return dp[n];
}
};leetcode 测试结果:
5、不同路径(medium)
a、解题思路
看我们题目后,根据经验此题位动态规划解题
1、转态表示
首先我们想以i,j位置为结尾表示什么
dp[i][j表示:以i,j位置结尾的时候,机器人到这里有多少条路径
2、状态转移方程
根据最近的一个位置划分
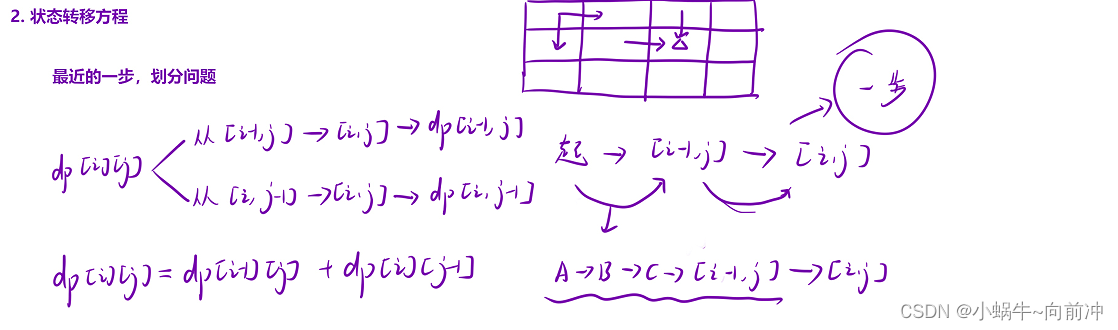
我要求到[i,j] 路径,本质上就是求dp[i - 1][j] + dp[i][j - 1]的路径和
所以状态转移方法为
3、初始化

这里我们要初始化,就是在二维数组多开一行和一列,但我们要思路多开的行列填什么呢(一切都是为了填表走服务)?,很明显,在根据dp[i][j] = dp[i-1][j]+dp[i][j-1];填写表格的时候,走一步就到终点,那最外层从从到都应该填1(dp[i][j表示:以i,j位置结尾的时候,机器人到这里有多少条路径),为达到这不目的,应该把dp[0][1]=1其余为0。
4、 填表顺序
从上往下填写每一行,每一行都是从左往又开始填写
5、返回值
dp[m][n]
b、代码
class solution {
public:
int uniquepaths(int m, int n)
{
//创建二维dp表
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
//初始化
dp[0][1] = 1;
//填表
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m][n];
}
}; leetcode 测试结果: 


发表评论