
1.链表常用技巧和操作总结
常用技巧
- 便于处理边界情况
- 方便我们对链表操作
比如都会遇到到这种题,前两句必须放前面,不然链表就断开了。但是我们可以定义一个next,这样就不用管按什么顺序了。
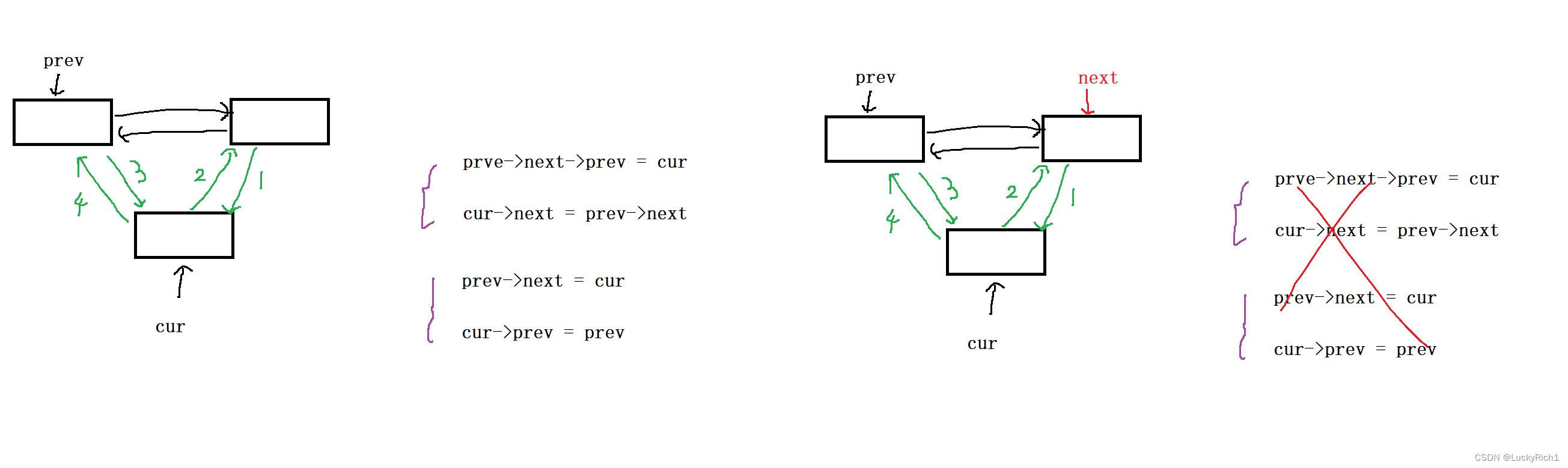
判环,找链表中环的入口,找链表中倒数第 n 个节点,都是用快慢指针解决的。
链表中的常用操作
2.两数相加
题目链接:2. 两数相加
题目分析:
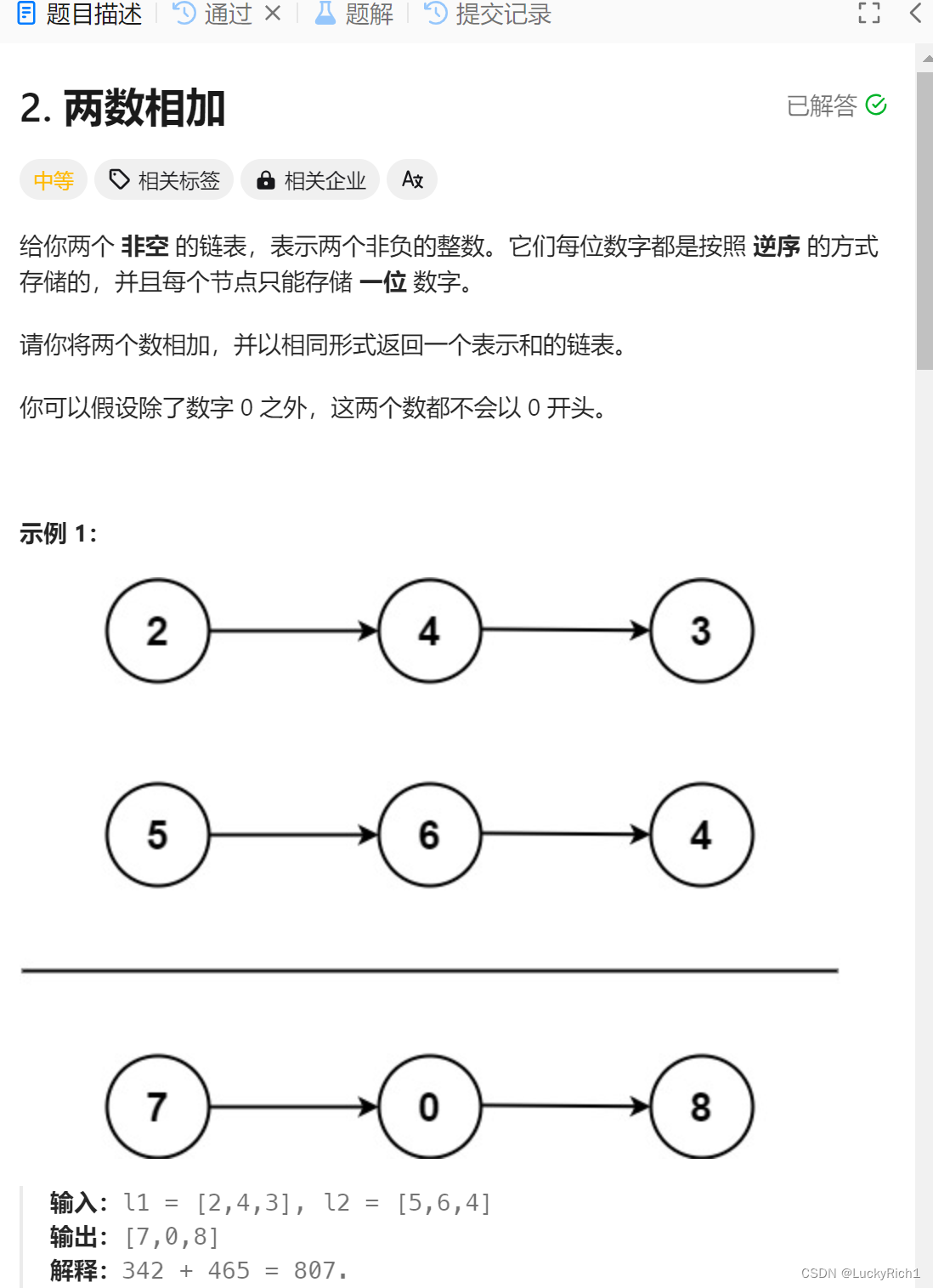
给两个链表,注意是逆序的。将两个数相加,还以逆序方式返回一个表示和的链表。
这道题给逆序正好方便我们从低位相加,如果是正序给的还要把链表逆置一下。
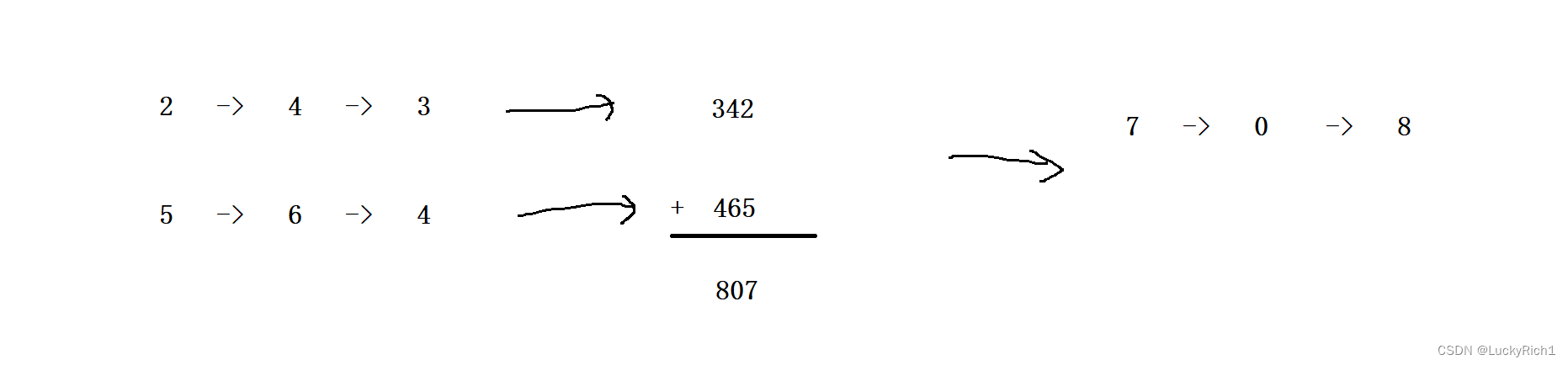
算法原理:
解法:模拟两数相加的过程即可
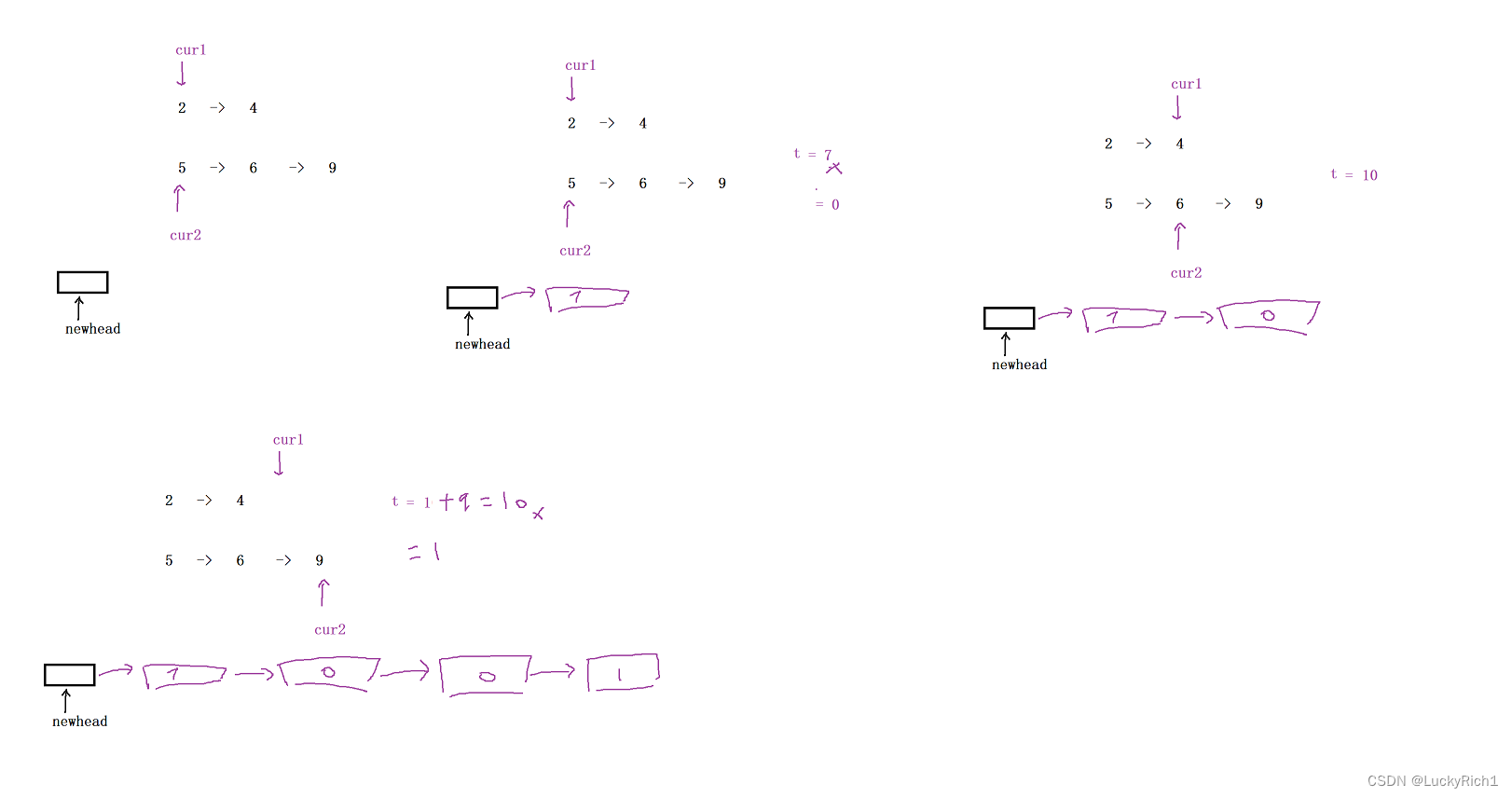
我们先来一个虚拟头结点,这样就少了判断为空的情况,直接尾插即可!在来一个 t 表示进位。t = cur1->val + cur2->val,每次都拿个数位构建节点。
class solution {
public:
listnode* addtwonumbers(listnode* l1, listnode* l2) {
listnode* newhead, *tail;
newhead = tail = new listnode;//创建一个虚拟节点记录最终结果
listnode* cur1 = l1, *cur2 = l2;
int t = 0; // 记录进位
while(cur1 || cur2 || t)
{
// 先加上第一个链表
if(cur1)
{
t += cur1->val;
cur1 = cur1->next;
}
// 加上第二个链表
if(cur2)
{
t += cur2->val;
cur2 = cur2->next;
}
tail->next = new listnode(t % 10);
tail = tail->next;
t /= 10;
}
//防内存泄漏
// tail = newhead->next;
// delete newhead;
// return tail;
return newhead->next;
}
};
4.两两交换链表中的节点
题目链接:24. 两两交换链表中的节点
题目分析:
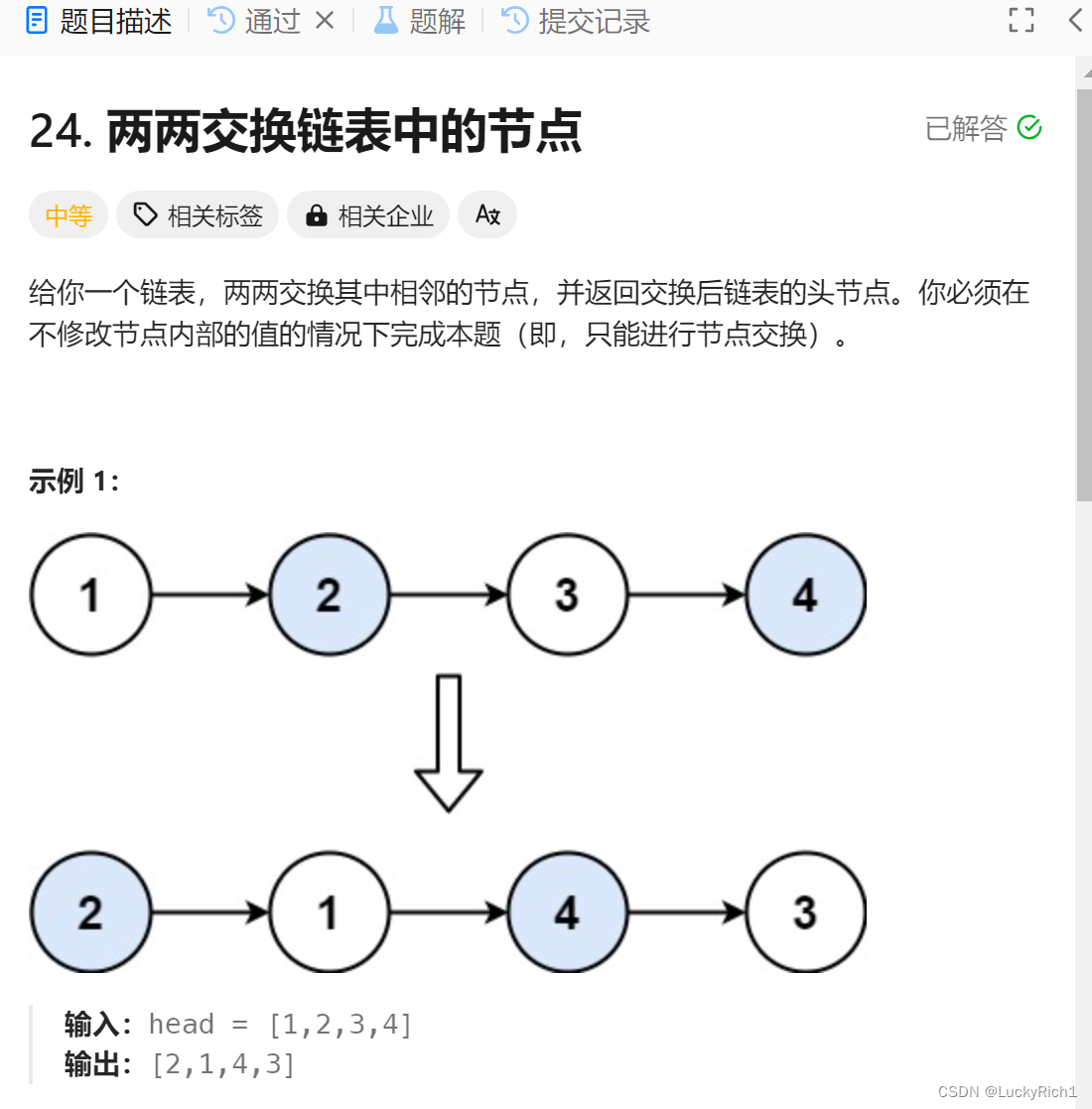
两两交换链表的节点,注意不能直接交换里面的值,只能修改指针。这道题在递归、搜索回溯专题用递归的方法解决。这里用循环迭代的方式。
算法原理:
解法一:递归
解法二:循环、迭代(模拟)
引入一个头节点,这样就减少判断边界的问题。如果不引入,交换前两个节点和后面的节点写法是不一样的,因为还要返回头指针,所以就只能先处理前两个找到最终返回的头节点,然后在处理后面的。这样太麻烦了。引入头节点,因为已经有了头节点所有后面处理逻辑都是一样的。
因为我们要两两交换,这里我们需要四个指针。不要吝啬空间,大胆去定义变量 ,这样交换指针的时候,不用担心代码顺序导致找不到链表的问题,有了这四个指针随便先写那一步。交换之后指针都移动一下。
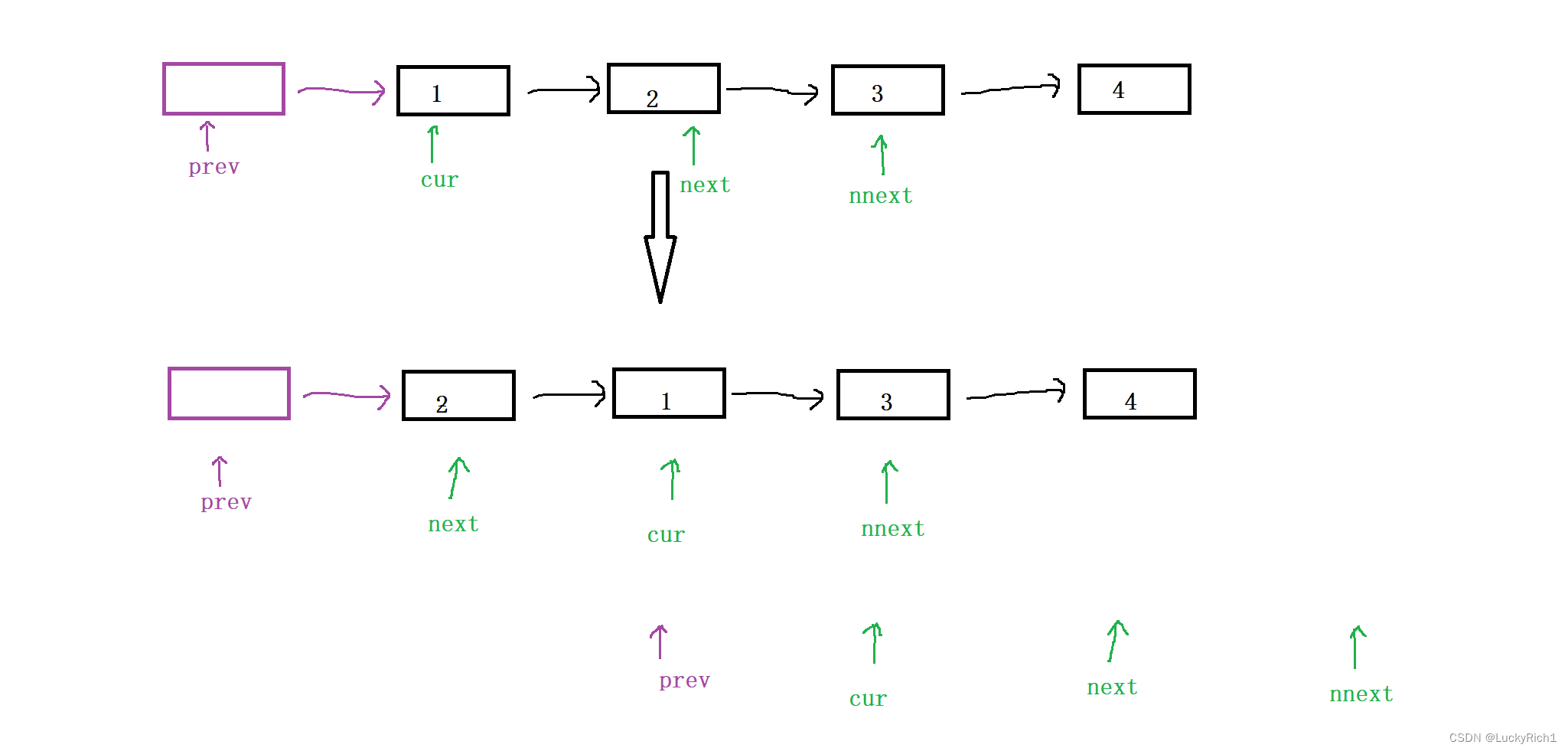
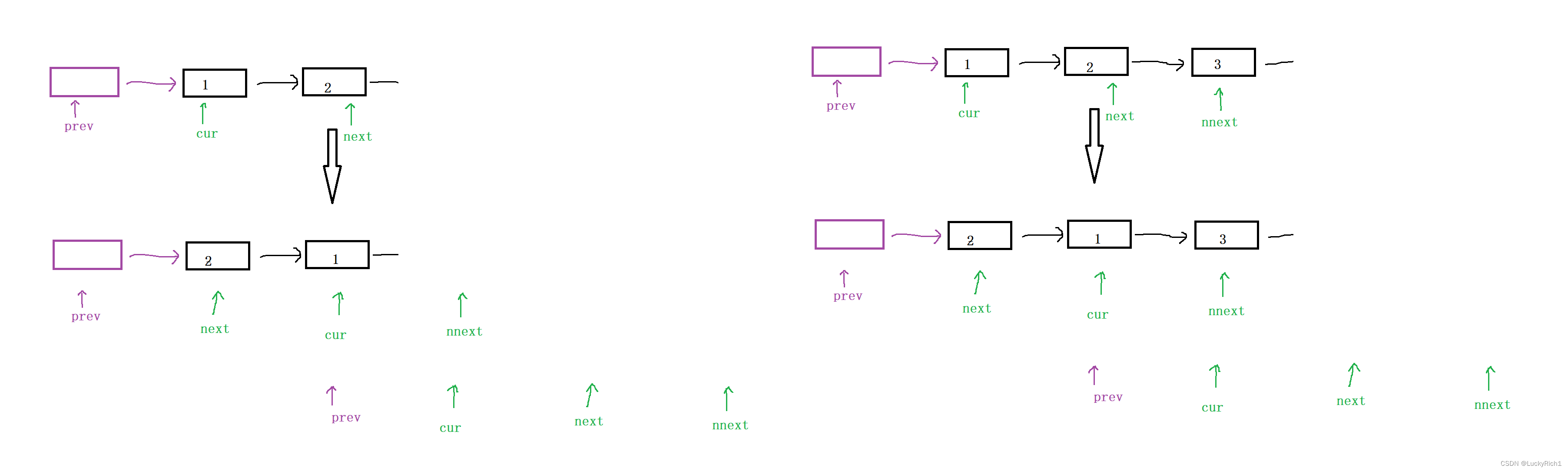
什么时候结束呢?节点可能有奇数个,也可能有偶数个。
可以看到当cur或者next为空的时候就结束了。
class solution {
public:
listnode* swappairs(listnode* head) {
if(head == nullptr || head->next == nullptr) return head;
listnode* newhead = new listnode;
newhead->next = head;
listnode* prev = newhead, *cur = head, *next = head->next, *nnext = head->next->next;
while(cur && next)
{
// 交换节点
prev->next = next;
next->next = cur;
cur->next = nnext;
// 修改指针,注意nullptr指针解引用
prev = cur;
cur = nnext;
if(cur) next = cur->next;
if(next)nnext = next->next;
}
return newhead->next;
}
};
4.重排链表
题目链接:143. 重排链表
题目分析:

给一个链表让按照规则重排一下。
算法原理:
解法:模拟
- 找到链表的中间节点
快慢指针 - 把后面的部分逆序
头插 - 合并两个链表
(合并两个有序链表)双指针

对于找到中间节点然后逆序,有两种做法。
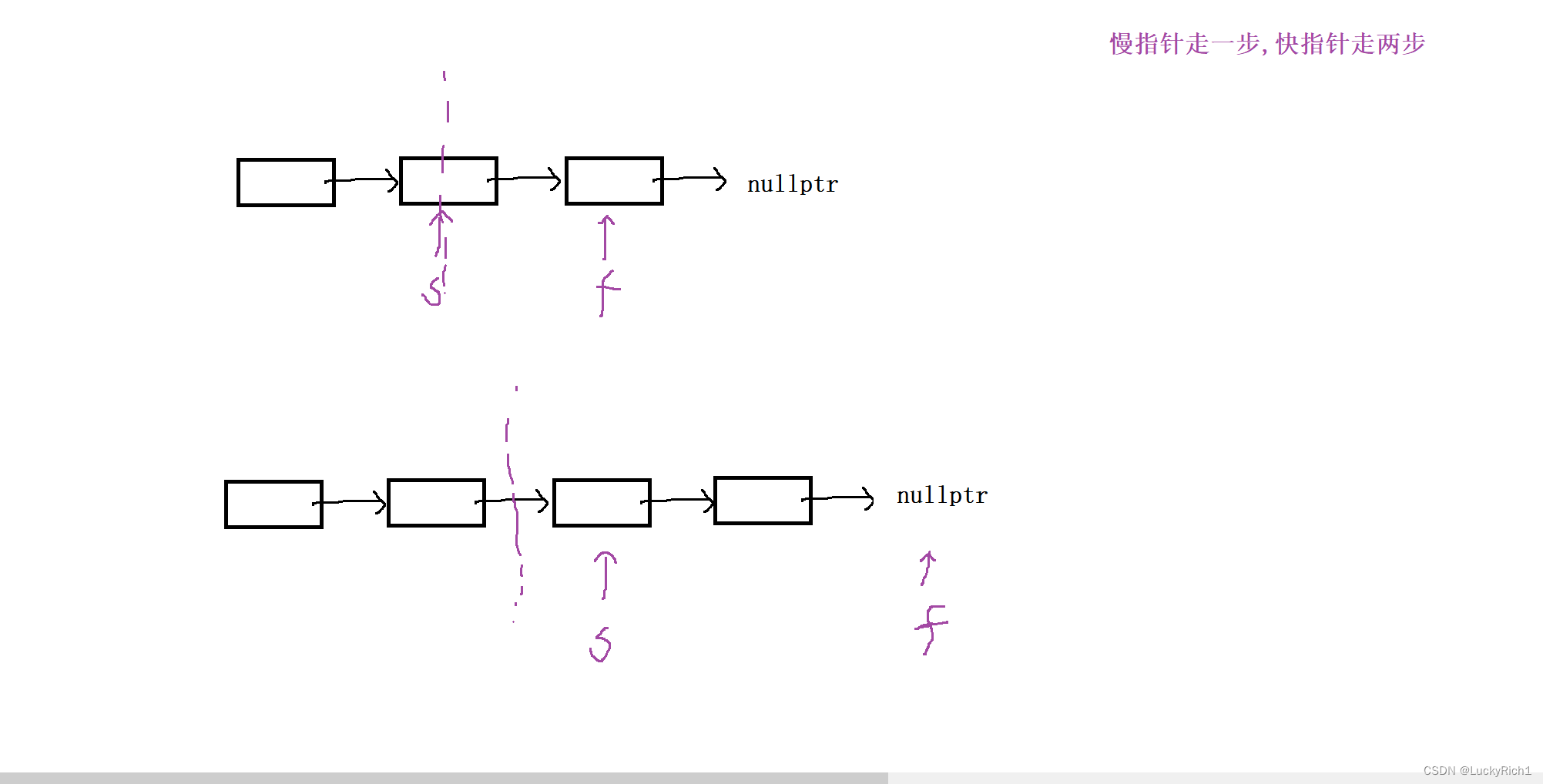
第一种逆序策略:slow->next 后面逆序
因为这道题比较特殊可以将slow->next 后面逆序,因为你会发现逆序完之后中间位置还是在一起的。因此可以大胆将slow节点给第一个链表。
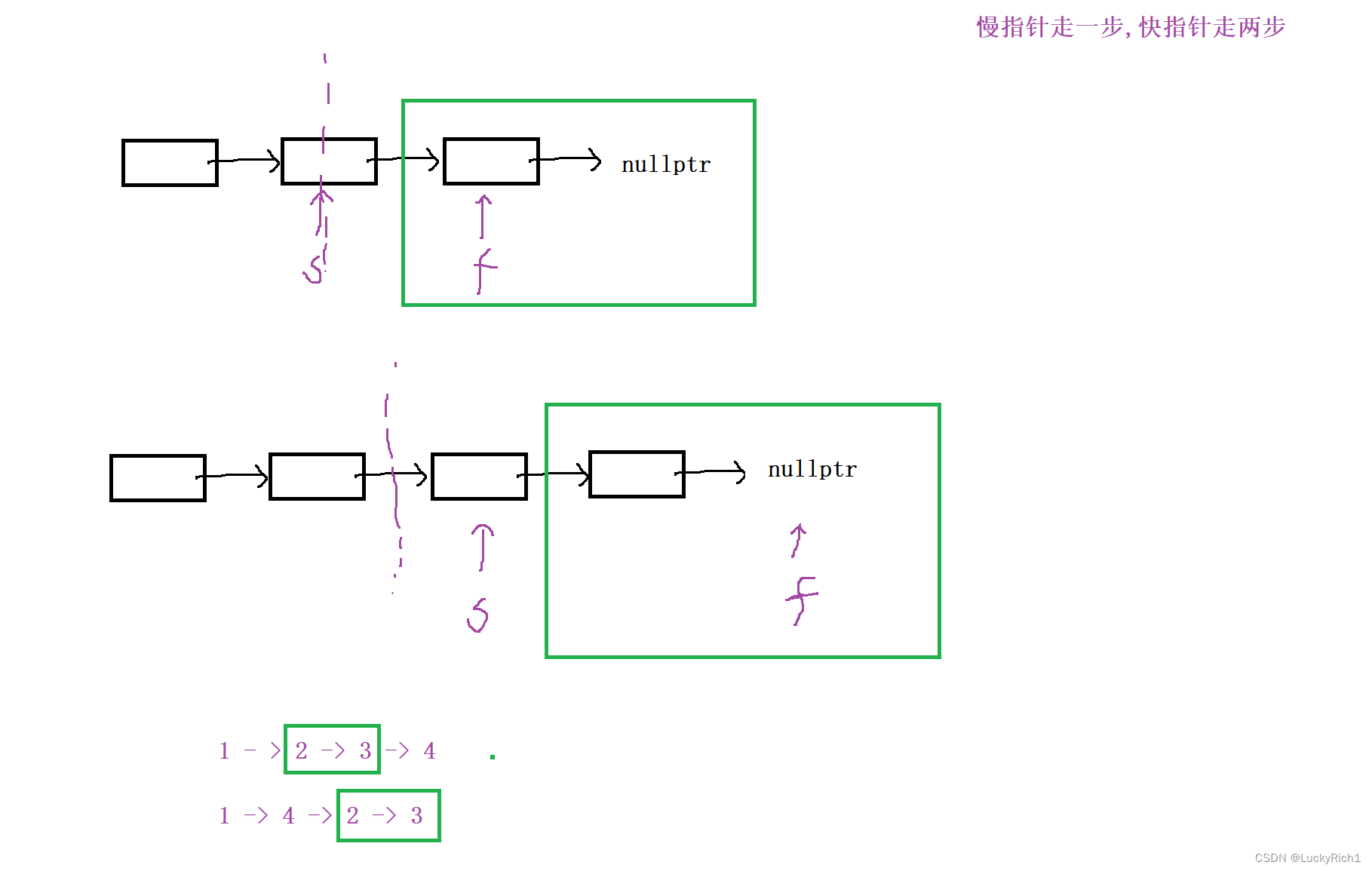
第二种逆序策略:从slow位置开始逆序
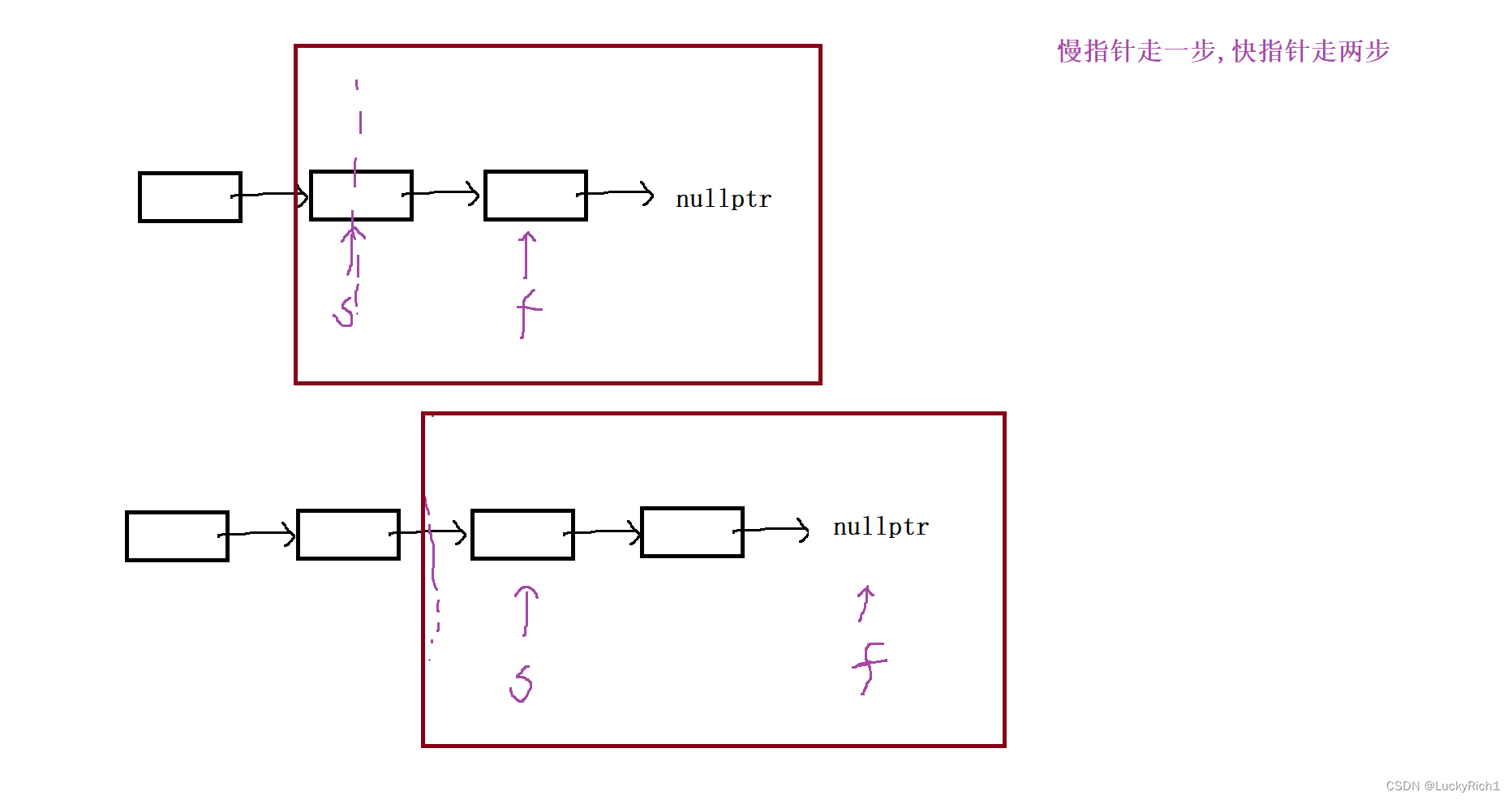
两种策略都是可以的。
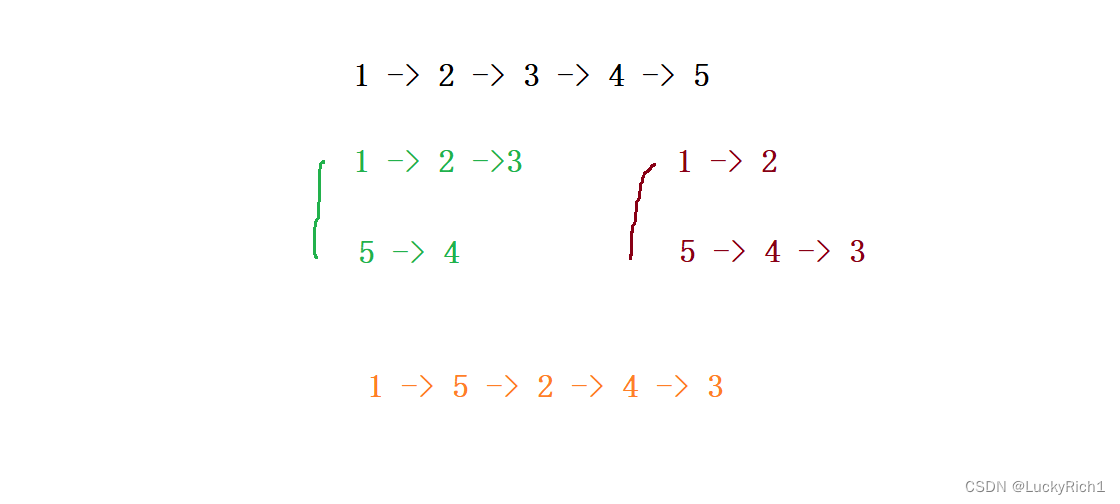
但是如果使用头插法逆序,建议还是第一种策略,因为我们是想让两个链表断开的。如果想逆序后链表还是在一起的,就用第二种策略。
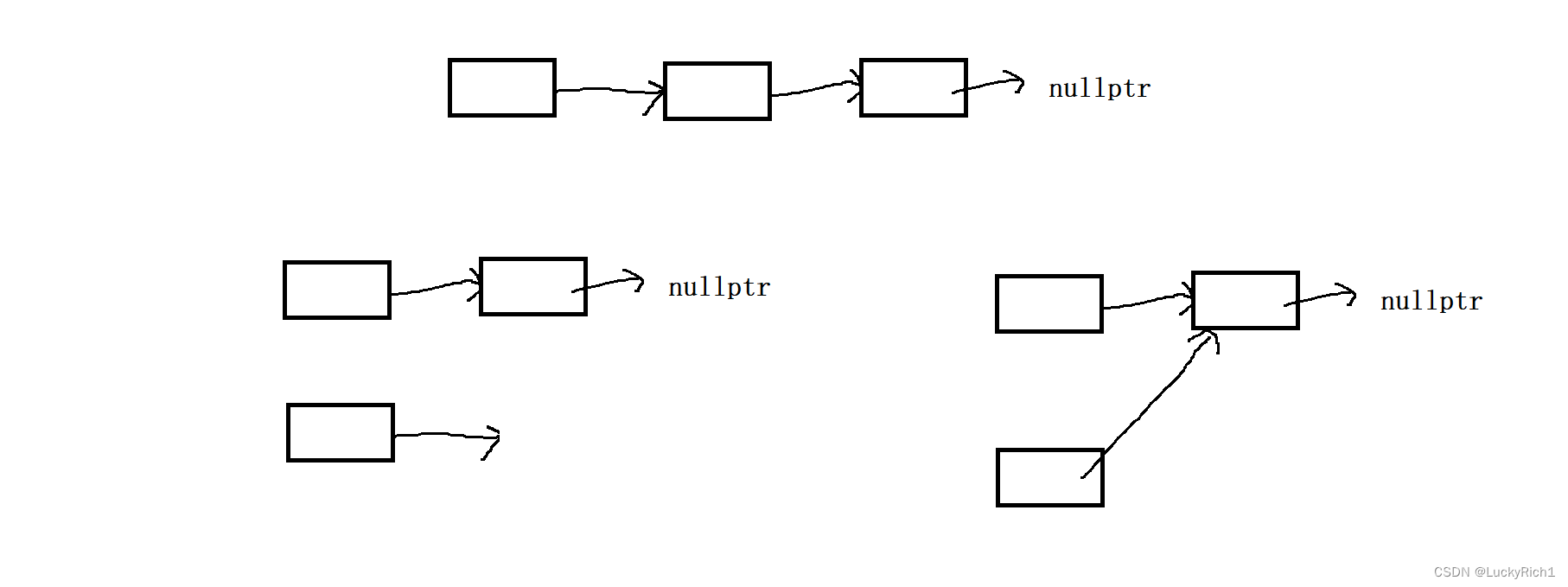
第一种策略
class solution
{
public:
void reorderlist(listnode* head)
{
// 处理边界情况
if(head == nullptr || head->next == nullptr || head->next->next == nullp
// 1. 找到链表的中间节点 - 快慢双指针(⼀定要画图考虑 slow 的落点在哪⾥)
listnode* slow = head, *fast = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
// 2. 把 slow 后⾯的部分给逆序 - 头插法
listnode* head2 = new listnode(0);
listnode* cur = slow->next;
slow->next = nullptr; // 注意把两个链表给断开
while(cur)
{
listnode* next = cur->next;
cur->next = head2->next;
head2->next = cur;
cur = next;
}
// 3. 合并两个链表 - 双指针
listnode* ret = new listnode(0);
listnode* prev = ret;
listnode* cur1 = head, *cur2 = head2->next;
while(cur1)
{
// 先放第⼀个链表
prev->next = cur1;
cur1 = cur1->next;
prev = prev->next;
// 再放第⼆个链表
if(cur2)
{
prev->next = cur2;
prev = prev->next;
cur2 = cur2->next;
}
}
delete head2;
delete ret;
}
};
第二种策略
class solution {
public:
void reorderlist(listnode* head) {
// 处理边界情况
if(head == nullptr || head->next == nullptr || head->next->next == nullptr) return;
// 1.找链表中间节点 -> 快慢指针(画图考虑slow的落点在哪里)
listnode* fast = head, *slow = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
// 2.将slow以及后面链表翻转 -> 头插法
listnode *cur = slow, *phead = nullptr, *next = nullptr;
while(cur)
{
next = cur->next;
cur->next = phead;
phead = cur;
cur = next;
}
// 3.合并两个链表 -> 双指针
listnode* newhead = nullptr, *tail = nullptr;
newhead = tail = new listnode(0);
int i = 1;
while(phead)
{
if(i%2 != 0)
{
tail->next = head;
tail = head;
head = head->next;
}
else
{
tail->next = phead;
tail = phead;
phead = phead->next;
}
++i;
}
head = newhead->next;
delete newhead;
}
};
5.合并 k 个升序链表
题目链接: 23. 合并 k 个升序链表
题目分析:

前面学过合并两个有序链表,现在有k个有序链表让合并一下。
算法原理:
解法一:暴力求解
利用合并两个有序链表思想,可以先让前两个链表合并成一个新的链表,然后拿新的链表在和下一个链表合并。。。。直到把所有链表合并完。
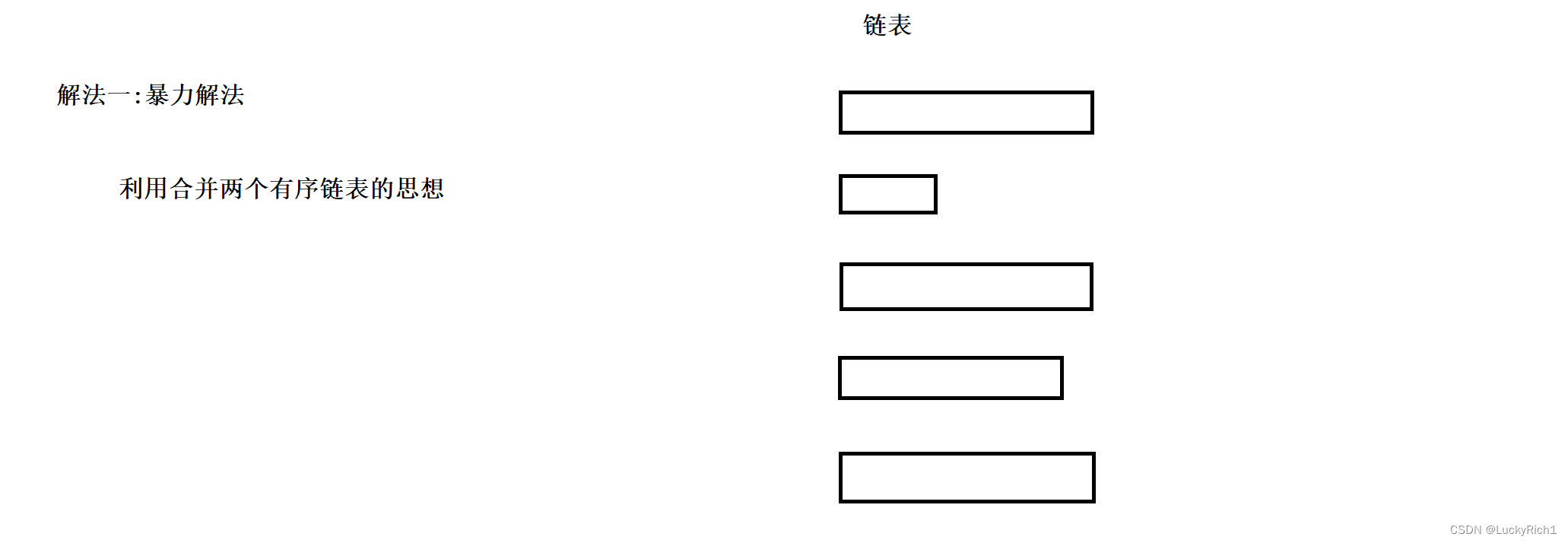
但是时间复杂度很恐怖,假设每一个链表长度为n,共有k个链表。看合并几次有序链表。如果是第一个链表,需要合并k-1次,并且长度为n,所以第一个链表 时间复杂度 n(k-1)。第二个链表n(k-2)。。。所以最终时间复杂度为o(nk^2)
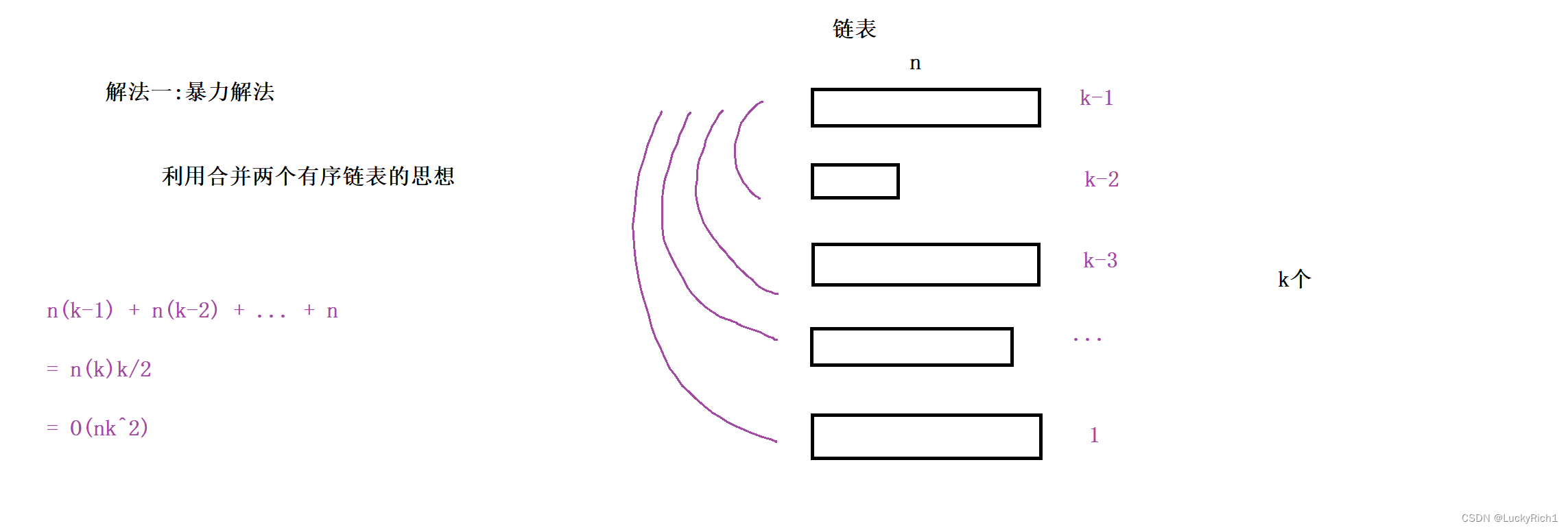
解法二:利用优先级队列做优化
合并k个有序链表,我们可以仿照合并两个有序链表的逻辑。先不考虑优先级队列,考虑如何对上面的做优化。
我们仿照合并两个有序链表的逻辑,先定义k个指针指向每一个链表,找出这个k个指针中值较小的节点,放在newhead的后面,放完之后,让这个指针往后移动。然后继续比较这k个指针指向的节点。这正好就是合并两个有序链表的逻辑。k个链表就k个指针,谁小谁就先连接newhead后面。
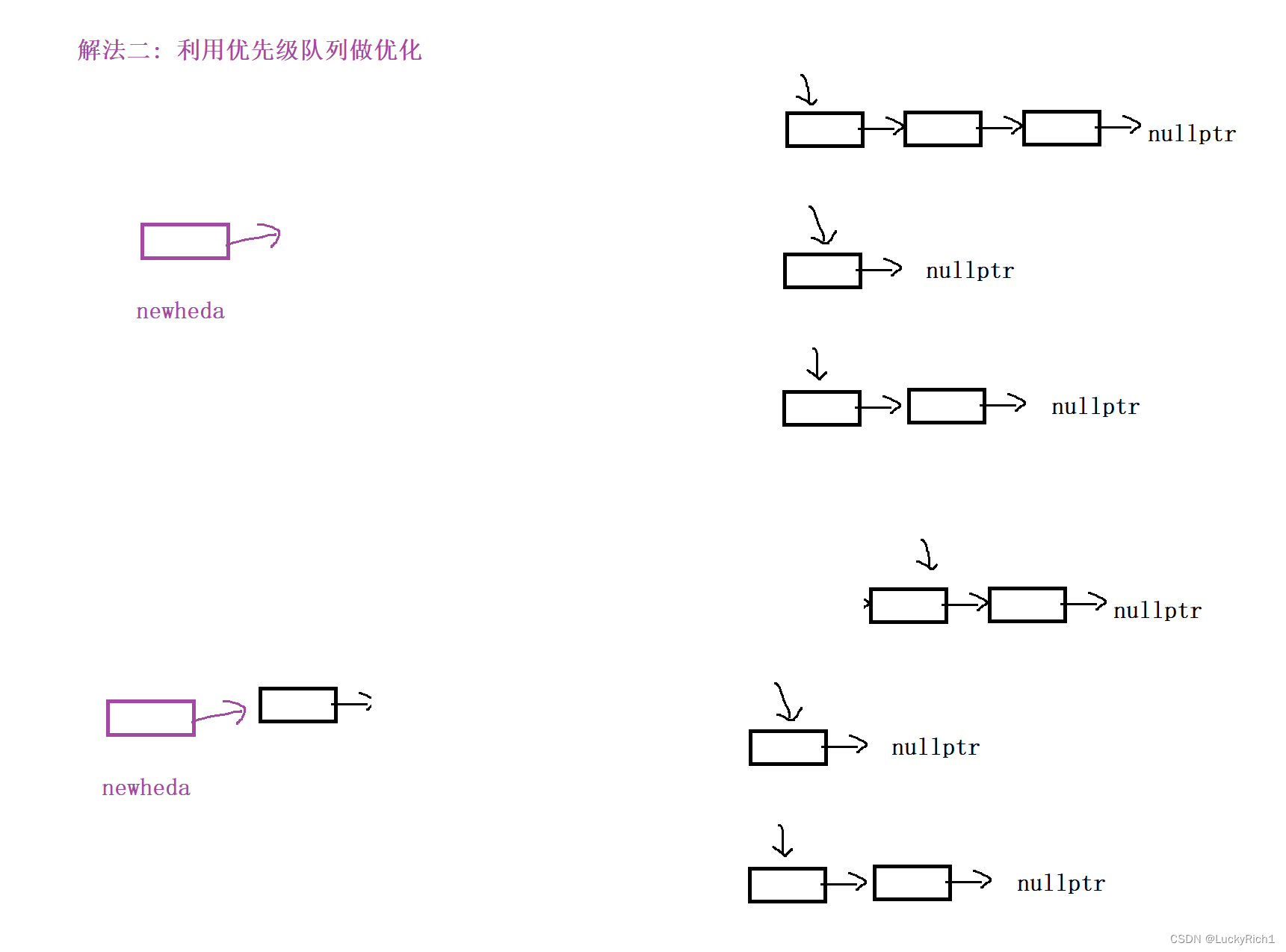
如何快速找到谁是k个节点中谁是较小的那个呢?
利用优先级队列。
因此我们的最终策略就是,搞一个小根堆,先将k个指针先丢到小根堆里,堆顶放的节点就是接下来我们要连接到newhead后面的节点。将堆顶节点连接到newhead后面之后,让这个指针往后移动然后进入优先级队列。此时堆顶也还是k个指针中最小的节点。。。。直到指针到空就不让这个链表进入队列了。等到所有链表的指针都到空了。说明链表合并结束了。
堆每次调整logk,一共进入nk个,所以这个时间复杂度o(nklogk)
class solution
{
public:
//类中的仿函数不能支持我们将最小节点放在栈顶
//因此指针并不是递增
//所以自己定义一个仿函数用来支持将最小节点放在栈顶
struct greater
{
bool operator()(const listnode* x,const listnode* y)
{
return x->val > y->val;
}
};
listnode* mergeklists(vector<listnode*>& lists)
{
if(lists.empty()) return nullptr;
listnode* newhead = new listnode;
listnode* tail = newhead;
priority_queue<listnode*,vector<listnode*>,greater> pq;
for(int i = 0; i < lists.size(); ++i)
{
if(lists[i])
pq.push(lists[i]);
}
while(!pq.empty())
{
// 出
listnode* cur = pq.top();
tail->next = cur;
tail = cur;
pq.pop();
//进
if(cur->next)
pq.push(cur->next);
}
return newhead->next;
}
};
解法三:分治 - 递归
利用归并排序。
假设有6个链表,让把这6个合起来成一个有序链表。此时可以沿着中间将6个链表一分为二,左边三个链表,右边三个链表,现让左边三个合并成一个链表,然后在让右边三个合并成一个链表。然后拿着这个两个有序链表,在合并成一个有序链表。
两个有序链表,在合并成一个有序链表。我们是非常熟悉的。
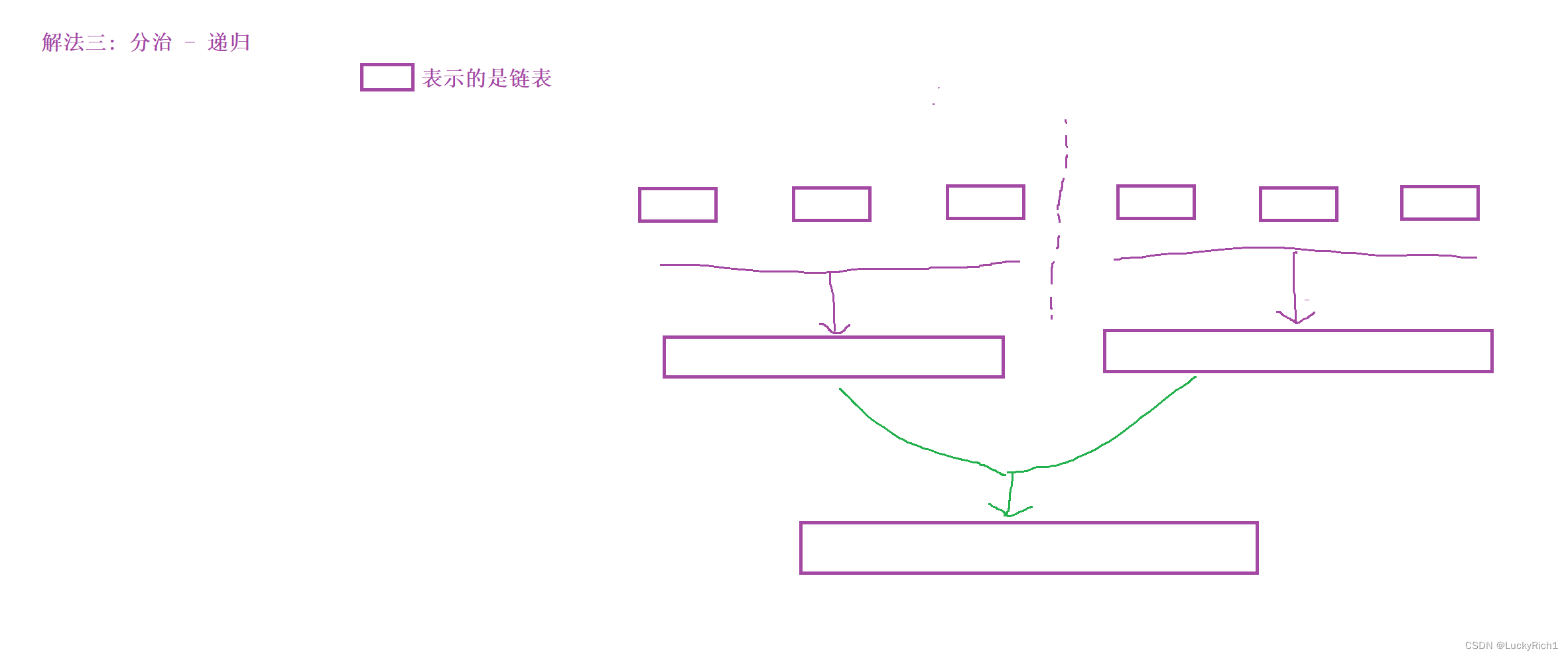
现在重点就是上面的让左边三个合并成一个,右边三个合并成一个,应该怎么做呢?
其实是和这个大过程是一样的。以左边三个为例,策略和上面一样。把三个链表从中间分开。先左边一个合并成一个有序链表,在让右边两个合并成一个有序链表。然后在把这两个链表合并成一个有序链表。左右可以再分。逻辑是一模一样的,这整体就是一个递归过程!

此时我们就可以用递归来实现这个策略。并且和归并排序过程是一样的。
归并排序先分然后才合,时间复杂度我们紧盯每一个链表节点执行多少次。分就是一个完全二叉树。每一个链表都会合并,合并次数是这个数的高度次,假设有k个链表树高度logk,每一个链表都执行logk合并,一共有k个链表,每一个链表有n个节点,所以时间复杂度o(nklogk)
class solution
{
public:
listnode* mergeklists(vector<listnode*>& lists)
{
return mergesort(lists, 0, lists.size() - 1);
}
listnode* mergesort(vector<listnode*>& lists, int left, int right)
{
if(left > right) return nullptr;
if(left == right) return lists[left];
int mid = left + (right - left) / 2;
listnode* newhead1 = mergesort(lists, left, mid);
listnode* newhead2 = mergesort(lists, mid + 1, right);
listnode* newhead = new listnode;
listnode* tail = newhead;
listnode* cur1 = newhead1, *cur2 = newhead2;
while(cur1 && cur2)
{
if(cur1->val < cur2->val)
{
tail->next = cur1;
tail = cur1;
cur1 = cur1->next;
}
else
{
tail->next = cur2;
tail = cur2;
cur2 = cur2->next;
}
}
if(cur1)
tail->next = cur1;
if(cur2)
tail->next = cur2;
tail = newhead->next;
delete newhead;
return tail;
}
};
6.k 个一组翻转链表
题目链接:25. k 个一组翻转链表
题目分析:
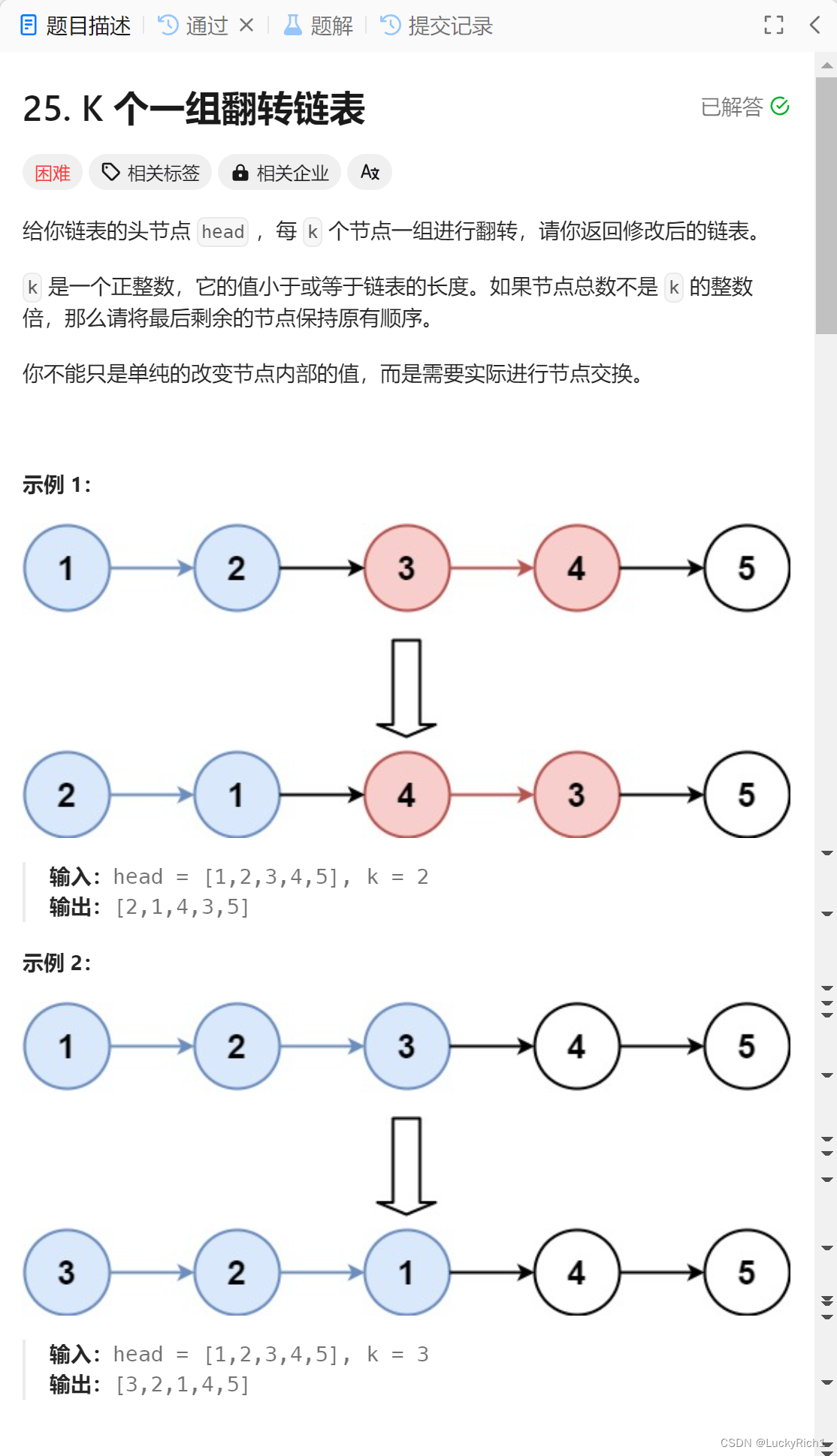
前面有一道题是两两一组翻转链表,现在是让k个一组翻转链表,小于k的就不用翻转了。
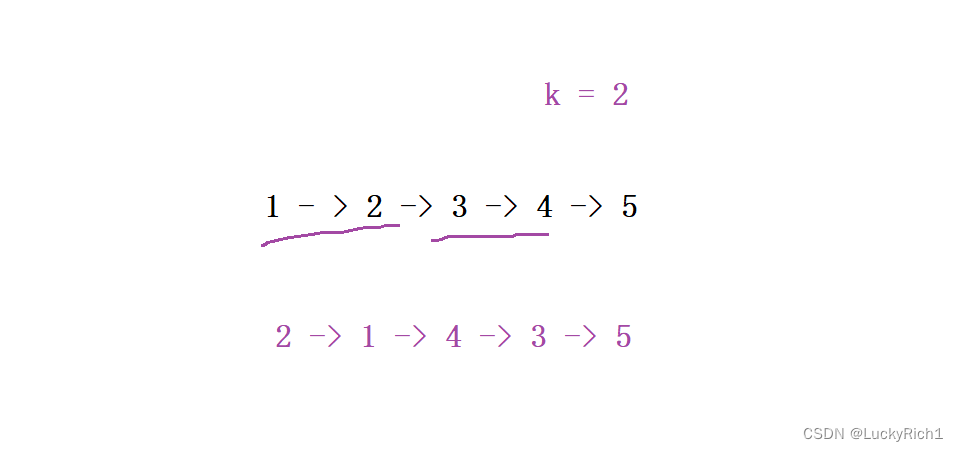
算法原理:
解法:模拟
- 先求出需要逆序多少组: n
- 重复 n 次,长度为 k 的链表的逆序即可(头插法)
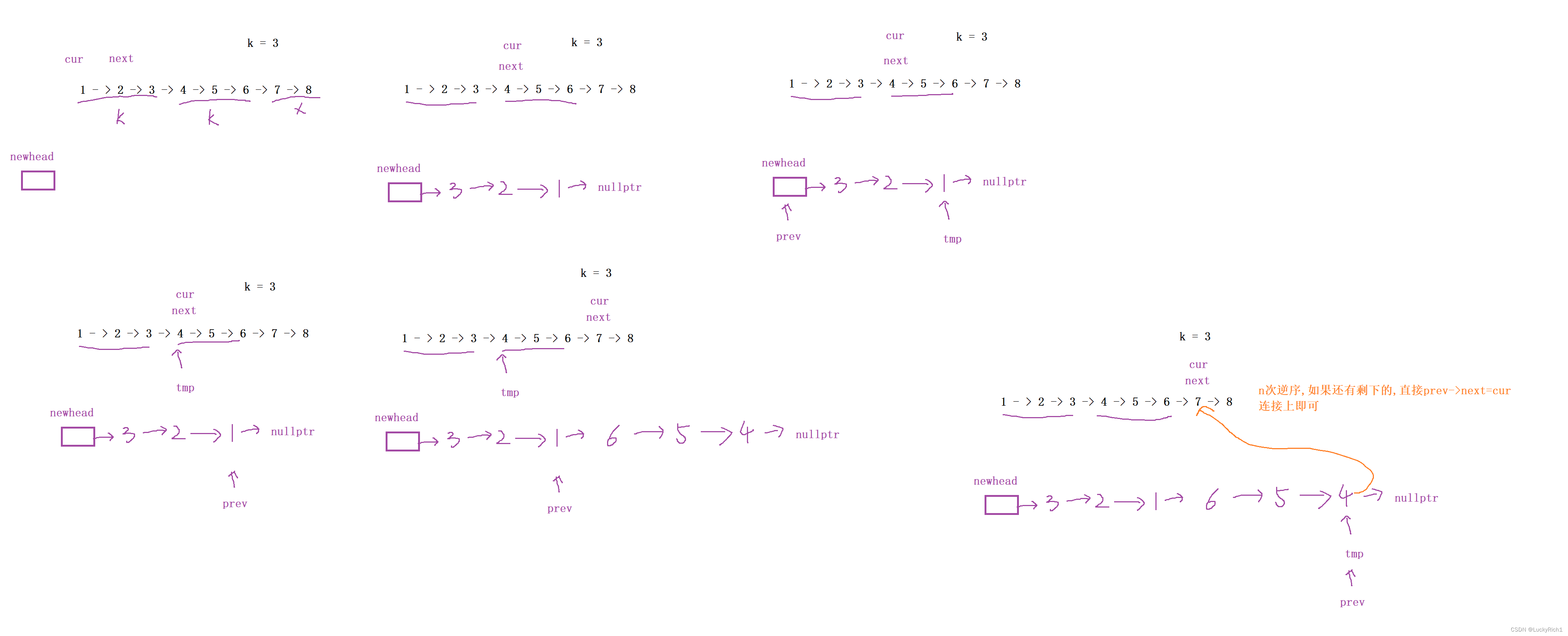
先求出需要逆序多少组: n,剩下的就不逆序了,直接连接上就好了。申请一个头结点newhead,把k个节点头插到newhead后面即可。注意这只是第一组,下一组也要头插怎么办?因此我们需要一个tmp指针记录下一次执行头插的头结点在哪,prev在一次头插结束之后就更新一下 prev = tmp ,prev指向充当头结点。
class solution {
public:
listnode* reversekgroup(listnode* head, int k) {
// 1.先求出需要逆序多少组
int n = 0;
listnode* cur = head;
while(cur)
{
++n;
cur = cur->next;
}
n /= k;
// 2.重复 n 次: 长度为 k 的链表逆序即可
listnode* newhead = new listnode;
listnode* prev = newhead;
cur = head;
for(int i = 0; i < n; ++i)
{
listnode* tmp = cur;
for(int j = 0; j < k; ++j)
{
listnode* next = cur->next;
cur->next = prev->next;
prev->next = cur;
cur = next;
}
prev = tmp;
}
// 3.把不需要翻转的接上
prev->next = cur;
prev = newhead->next;
delete newhead;
return prev;
}
};


发表评论