atcoder beginner contest 250
g
链接
题目大意
给的一个长度为n的物品的价值的序列,a1,a2,a3……an,每次操作可以选择购买或卖出,也可以什么都不操作,求最后获得的利润的最大值。
数据范围 1<=ai<=1e9,n<=2e5
思路
这题一开始我觉得很像一道leetcode的动态规划 ——买卖股票的最佳时机ii 但是仔细看了一下发现不对,因为这道题可以持有多股(原题只能持有一股),也就是这题用动态规划的话,转移方案会有多种,详细如下:
void solve() {
int n;
cin >> n;
vector<int>a(n + 1);
for (int i = 1; i <= n; ++i) {
cin >> a[i];
}
//这里的dp[i][j]表示第i天持有j个股票的最大利润
vector<int> dp0(n + 1, -inf),dp1(n + 1, -inf);//采用滚动数组优化空间,以为只能从i-1转移
dp0[0] = 0;
dp0[1] = -a[1];
int res = 0;
for (int i = 2; i <= n; ++i) {
for (int j = 0; j <= i; ++j) {
dp1[j] = dp0[j]; //不操作
if (j >= 1) dp1[j] = max(dp1[j], dp0[j - 1] - a[i]); //买入
if (j + 1 <= n) dp1[j] = max(dp1[j], dp0[j + 1] + a[i]); //卖出
res = max(res, dp1[j]);
}
dp0 = dp1; //滚动
}
cout << res << endl;
}
毫无疑问,o(n²)的时间复杂度对于n<=2e5的题目会tle,需要优化,而优化dp又是一个复杂的问题,常见的优化有:单调队列优化、优先队列优化等等。优化算法需要的时间和思维成本太大,故这题需要换一种方法。
做法
这题是一道反悔贪心的经典题
反悔贪心通常需要创建一个堆,然后再堆内进行贪心,对堆进行操作,如(pop,push)等等。反悔贪心的精髓就是,对于当前的最优解直接记录它对答案的贡献,而后续遇到更优解时只需要更新上一次最优解(因为堆自动排序了,所以更新只需要在o(1)的时间复杂度内完成)。注意的是,更新最优解后,仍然需要把当前的值放入队列中,因为它本身也能够被更新。
让我们看看只放入更新的结果,不放入自身的情况:
例如:对于 2 5 9 9这个序列,不放入自身进行反悔贪心的话,优先队列依次是这样的:
[2] ->[5]->[9]->[9,9]
对答案的贡献为:
[0]->[0+3]->[0+3+4] =7
容易发现贪心的结果不对,正解为11
所以正确的优先队列应该是这样:
[2] ->[5,5]->[5,9,9]->[9,9,9,9]
对答案的贡献为:
[0]->[0+3]->[0+3+4]->[0+3+4+4] =11
正如上文所说
代码
void solve() {
int n;
cin >> n;
vector<int> a(n + 1);
for (int i = 1; i <= n; ++i) {
cin >> a[i];
}
priority_queue<int, vector<int>, greater<int>>pq;
int res = 0;
pq.push(a[1]);
for (int i = 2; i <= n; ++i) {
if (a[i] > pq.top()) { //反悔,更新上一次的最优解
res += a[i] - pq.top(); //添加上对答案多的贡献
pq.pop();
pq.push(a[i]);
}
pq.push(a[i]); //注意这里
}
cout << res << endl;
}
时间复杂度
o(nlog2n)
标签
贪心、优先队列
rating
cf1500左右吧
小结
2024-4-12:
这题赛事我没开出来,但是想到了用优先队列反悔贪心了,但是贪心地不对,因为没有放入两次,长记性了!最后动态规划去优化了一晚上,可惜了。
educational codeforces round 149 (rated for div. 2)
d
链接
题目大意
给定一个字符串序列,序列中只有‘(’和‘)’,认为一个序列是好的,有且仅当序列的所有前缀左括号的数量大于等于右括号的数量,或有括号的数量大于等于左括号的数量,并且这个序列中左右括号总数相同。可以对序列中的每个括号染色,同一个颜色的分为一组,每一组都应该是好的序列,求最小分组数,无法分组则输出-1
思路
括号匹配的题目大概率可以用栈(stack)来做,但这题其实没必要。对这种括号问题的一个经典做法是吧左括号看做1,把右括号看做-1,求一下前缀和,然后再按照题意去操作即可。
做法
对于这题,需要求最小分组数,我们可以贪心地想一想,然后会发现,排除去不存在的情况(左括号和右括号数量不同),那么序列最多可以被分成两组,为什么呢?其实很简单,对于前缀和,最终结果肯定是0,那么对于前缀和中大于等于0的部分,我们可以染成一个颜色,小于0的部分都染成另一个颜色。因为,我们把题目再翻译一下,左括号数量大于右括号数量,也就是说左括号和右括号的和大于等于0(因为我们把左括号看做1,右括号看做-1),那么另一个情况也是如此。注意判断边界情况,即染成第一种颜色的边界条件是a[i]>=0&&a[i-1]>=0。
如下图:
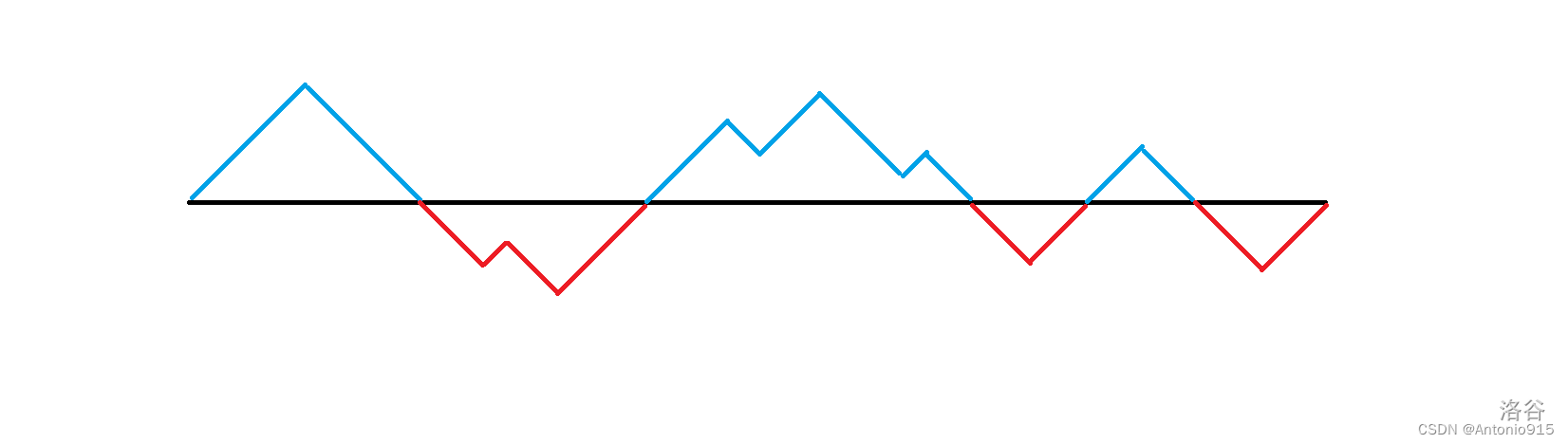
(图是从洛谷搬的),有兴趣的也能看看大佬的题解:
[cf1837d] bracket coloring - 洛谷专栏
代码
void solve() {
int n;
cin>>n;
int cnt1=0,cnt2=0;
vector<int>a(n+1);
for(int i=1;i<=n;++i){
char ch;
cin>>ch;
cnt1+=ch=='(';
cnt2+=ch==')';
int tt=(ch=='('?1:-1); //转换括号为1,-1
a[i]=tt+a[i-1]; //求前缀和
}
if(cnt1!=cnt2){ //判断不成立情况
cout<<-1<<endl;
return;
}
vector<int>res;
bool ok1=false,ok2=false;
for(int i=1;i<=n;++i){
if(a[i]>=0&&a[i-1]>=0){ //注意边界情况
res.push_back(1);
ok1=true;
}
else{
res.push_back(2);
ok2=true;
}
}
if(ok1&&ok2){ //分成两组
cout<<2<<endl;
for(auto &x:res) cout<<x<<" ";
cout<<endl;
}
else{ //分成一组
cout<<1<<endl;
for(int i=1;i<=n;++i) cout<<1<<" ";
cout<<endl;
}
}
时间复杂度
复杂度为o(nlog2n)。
标签
贪心、前缀和,栈
rating
1400
小结
2024-4-12
大佬眼中的经典问题,确实我需要学习的新知识,括号匹配转换成1和-1,求前缀和,这个思想真的很厉害。
codeforces round 872 (div. 1)
a
链接
题目大意
有n个人,m个位置,有3种人,第一种人只想坐在最右边的人的右边,如果最右边的人没有位置,则离场,如果没有人的话就坐在最左边。第二种人只想坐在最左边的人的左边,如果最左边的人没有位置,则离场,如果没有人的话就坐在最右边。第三种人只想坐在特定位置x。求最多有多少个位置可以坐人。
思路
可以发现,如果位置没人的时候,选择让第一种人先坐下,或者选择第二种人先坐下,那么另一种人就没有位置可以做了,那么这时的最佳方案就是max(第三种人+第一种人,第三种人+第二种人)。把整个条座位1-m看做一个数轴,那么第一种人从左到右坐,第二种人从右往左坐,当遇到第三种人时,先让他左下,然后再坐自己。因此,第三种人总是可以坐下。
此外,还需要枚举第三种人,然后计算他左右两边可以坐多少第一种人和第二种人,这里也要加上第三种人,因为他总是可以坐下。
做法
对于第一个方案,统计一下个数即可取大的即可。对于第二个方案,需要排序然后枚举,记得去重,排序后可以利用下标来寻找个数关系。
代码
void solve() {
int n,m;
cin>>n>>m;
vector<int>a;
int cnt1=0,cnt2=0;
for(int i=1;i<=n;++i){
int x;
cin>>x;
if(x>0) a.push_back(x);
cnt1+=x==-1; //统计第一种人
cnt2+=x==-2;//统计第二种人
}
sort(a.begin(),a.end()); //排序
a.erase(unique(a.begin(),a.end()),a.end()); //去重
int res=-inf;
res=max({res,min(cnt1+(int)a.size(),m),min(cnt2+(int)a.size(),m)}); //第一种法案
for(int i=0;i<a.size();++i){
res=max(res,min(a[i]-1,cnt1+i)+min(m-a[i],cnt2+(int)a.size()-i-1)+1); //枚举第三种人
}
cout<<res<<endl;
}
时间复杂度
复杂度为o(nlog2n)。
标签
贪心,模拟
rating
1400
小结
2024-4-13
这题还是挺简单的,只是记得处理一下边界条件和小细节就好。主要是样例给的好,基本情况都能覆盖了,样例能过基本就能ac了。
educational codeforces round 146 (rated for div. 2)
c
链接
题目大意
给定一个序列为n,机器人寻找第i个数的次数,有两个机器人,每次搜索的时间是s1,s2,你需要构造两个序列a,b使得总的搜索时间最短。
思路
这题是求最值问题的构造问题,因此我们可以考虑贪心地构造。我们发现,对答案的贡献是min(res1.size()*s1*a[i],res2.size()*s2*a[i]),这里res1和res2表示构造的序列,a表示原序列。注意,需要对序列从大到小排序,把次数多的先放入时间短的序列。
做法
排序后,枚举每一个次数,每次取最小的即可。
代码
void solve(){
int n,s1,s2;
cin>>n>>s1>>s2;
vector<pii>a(n+1);
for(int i=1;i<=n;++i){
cin>>a[i].first;
a[i].second=i;
}
sort(a.begin()+1,a.end()); //排序
vector<int>res1,res2;
for(int i=n;i>=1;i--){ //从大到小枚举
if(s1*((int)res1.size()+1)*a[i].first<=s2*((int)res2.size()+1)*a[i].first){
res1.emplace_back(a[i].second);
}
else{
res2.emplace_back(a[i].second);
}
}
cout<<res1.size()<<" ";
for(auto &x:res1) cout<<x<<" ";
cout<<endl;
cout<<res2.size()<<" ";
for(auto &x:res2) cout<<x<<" ";
cout<<endl;
} 数据范围
2≤n≤2⋅1e5; 1≤s1,s2≤10;1≤ri≤1e6
时间复杂度
复杂度为o(nlog2n)。
标签
贪心,排序,构造
rating
1500
小结
2024-4-13
感觉没有1500的难度,这题应该就1200左右,看懂了题直接就可以做了。


发表评论