
🔥博客主页:
📚系列专栏:
🌟人之为学,不日近则日退
❤️感谢大家点赞👍收藏⭐评论✍️
目录
🗒️前言
一、什么是数据结构
二、什么是算法
三、算法的效率
四、时间复杂度
时间复杂度的概念
4.1大o渐进表示法
推导大o阶方法:
另外有些算法的时间复杂度存在最好、平均和最坏情况:
- 最坏情况: 任意输入规模的最大运行次数(上界)
- 平均情况: 任意输入规模的期望运行次数
- 最好情况: 任意输入规模的最小运行次数(下界)
说明:在实际中一般情况关注的是算法的最坏运行情况。
4.2常见时间复杂度计算举例
🚩冒泡排序:
// 计算bubblesort的时间复杂度?
void bubblesort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
🚩二分查找
// 计算binarysearch的时间复杂度?
int binarysearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n - 1;
// [begin, end]:begin和end是左闭右闭区间,因此有=号
while (begin <= end)
{
int mid = begin + ((end - begin) >> 1);
if (a[mid] < x)
begin = mid + 1;
else if (a[mid] > x)
end = mid - 1;
else
return mid;
}
return -1;
}o(n)和o(log2n)的对比:
| n | 1000 | 100w | 10亿 |
| o(n) | 1000 | 100w | 10亿 |
| o(log2n) | 10 | 20 | 30 |
由此我们看到o(log2n)相对o(n)在效率上有很大的提升,但二分查找有一个限制条件就是数组必须有序,所以在实际中二分查找应用并不多。
🚩递归阶乘
// 计算阶乘递归fac的时间复杂度?
long long fac(size_t n)
{
if (0 == n)
return 1;
return fac(n - 1) * n;
}
📒时间复杂度:o(n)
🚩斐波那契数
// 计算斐波那契递归fib的时间复杂度?
long long fib(size_t n)
{
if (n < 3)
return 1;
return fib(n - 1) + fib(n - 2);
}
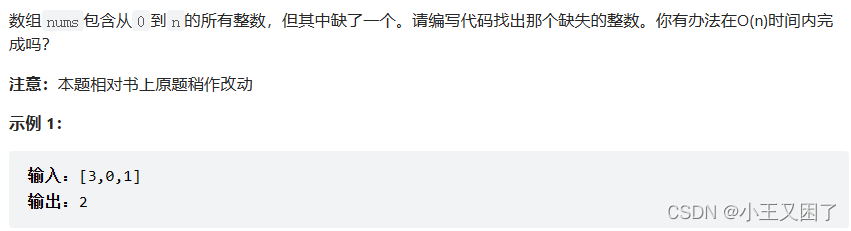
4.3例题:消失的数字
五、空间复杂度
空间复杂度的概念:
5.1空间复杂度计算
🚩递归阶乘:
// 计算阶乘递归fac的空间复杂度?
long long fac(size_t n)
{
if(n == 0)
return 1;
return fac(n-1)*n;
}
📒空间复杂度:o(n)
🚩 斐波那契数
long long fib(size_t n)
{
if(n < 3)
return 1;
return fib(n-1) + fib(n-2);
}
📒空间复杂度:o(n)
5.2例题:轮转数组

💡思路
- 逆置前n-k个
- 逆置后k个
- 整体逆置
void reverse(int* nums,int left,int right)
{
int tmp=0;
while(left<=j)
{
tmp=nums[left];
nums[left]=nums[right];
nums[right]=tmp;
left++;
right--;
}
}
void rotate(int* nums, int numssize, int k)
{
if(k==0)
{
return nums;
}
reverse(nums,0,numssize-1);
reverse(nums,0,k%numssize-1);
reverse(nums,k%numssize,numssize-1);
}






发表评论