【动态规划】最长上升子序列（单调队列、贪心优化）_Python

题目:最长上升子序列

题解:

代码实现:

完结撒花：

本篇是对最长上升子序列基础做法的一种优化，没有看过基础做法的uu们可以看看这篇：

题目:最长上升子序列

题解:

优化的做法与之前相比，适用范围更广，当数据范围大的时候，基础做法会tle。

但优化做法dp的思想却少了，更像是一种贪心，由于本题是从dp衍生出来的，所以仍然将其归为dp。

废话不多说。

朴素做法为，找到前一个小于当前值，将其最长上升子序列加一，就为当前值得最长上升子序列。

但观察每一个被插入得值，例如有以下五个数字

3和1都为上升序列为1的数组，但能插入到1上的一定能插到三的上面，反之却不一定。所以我们可以想象出，只要保存上升序列长度中最小的那个值最为末端就可以了。

例如这里的3和1都为长度为1的上升序列，但我们只要保存1.

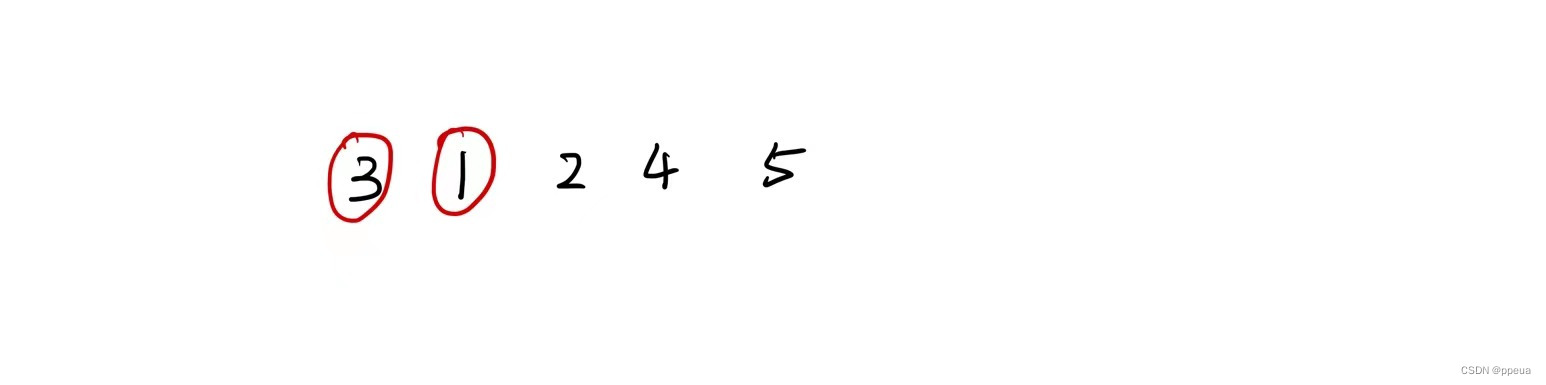
之后再将2插入到1上，此时更新上升序列长度为2的最后一个值为2.

4又可以插入到2后，所以更新长度为3的最后一个值为4。

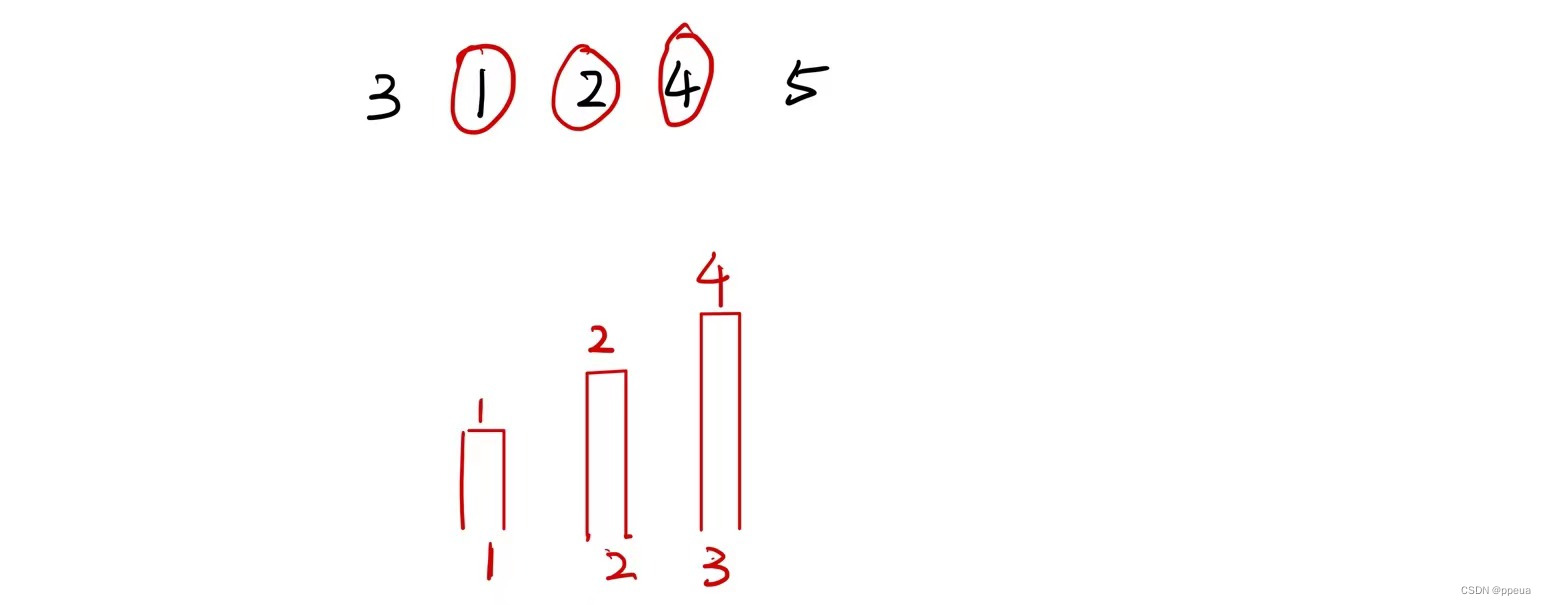
最后如图所示

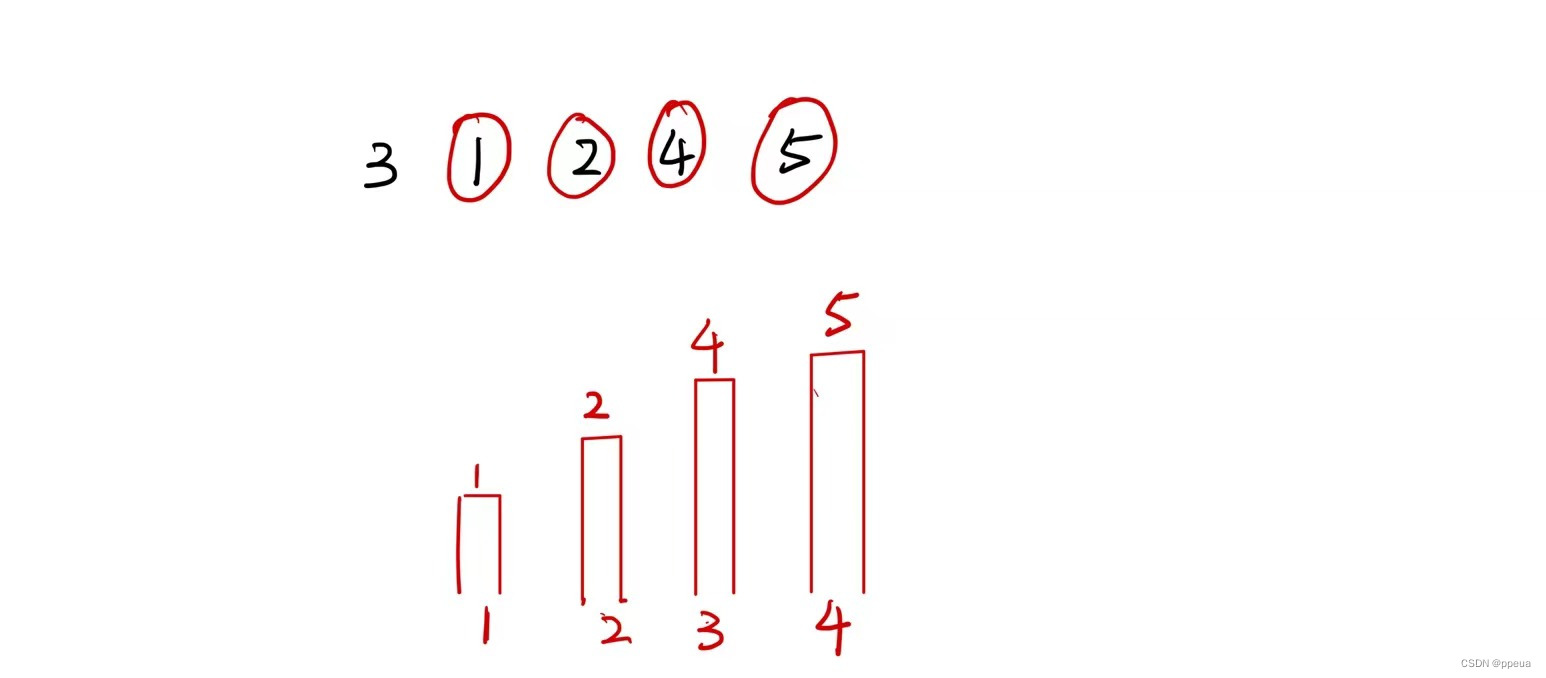
所以我们很容易就能归纳出上面的过程，找到最大小于待插入数的序列，在下一个位置更新其序列长度与队尾的值。

分析下代码实现，len为当前最长的子序列，利用二分查找寻找，最大的小于当前值x的位置，之后将下一个最长子序列的末位更新为x。循环往复即可

代码实现:

#include<iostream>
#include<algorithm>
using namespace std;
const int n=100010;
int n;
int a[n];
int q[n];

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>a[i];
    }
    int len=0;
    q[0]=-2e9;
    for(int i=0;i<n;i++)
    {
        int l=0,r=len;
        while(l<r)
        {
            int mid=l+r+1>>1;
            if(q[mid]<a[i])l=mid;
            else r=mid-1;
        }
        len=max(len,r+1);
        q[r+1]=a[i];
    }
    cout<<len;
    return 0;
}