线性回归
适合处理数值问题。
f
(
x
i
)
=
w
x
i
+
b
f(x_i)=wx_i+b
f(xi)=wxi+b使得
f
(
x
i
)
f(x_i)
f(xi)约等于
y
i
y_i
yi
离散属性的处理:若有序order,则连续化;否则需要通过编码,转化为k维向量
求解最优解:对
e
(
a
,
b
)
=
∑
i
=
1
m
(
y
i
−
w
x
i
−
b
)
2
e_{(a,b)}=\sum_{i=1}^{m}(y_i-wx_i-b)^2
e(a,b)=∑i=1m(yi−wxi−b)2进行最小二乘参数估计,分别对w和b求偏导,令等式为0,即可求出w和b。
解释为何一定是最优解?
因为在导数为0处,要么是局部极大要么局部极小,由于是求偏离的程度
e
(
a
,
b
)
e_{(a,b)}
e(a,b),它的极大值只会是无穷大,因此在导数为0处,再也不会再小了,就是取得极小的点。

多元线性回归


广义线性模型

对率回归logistic regression
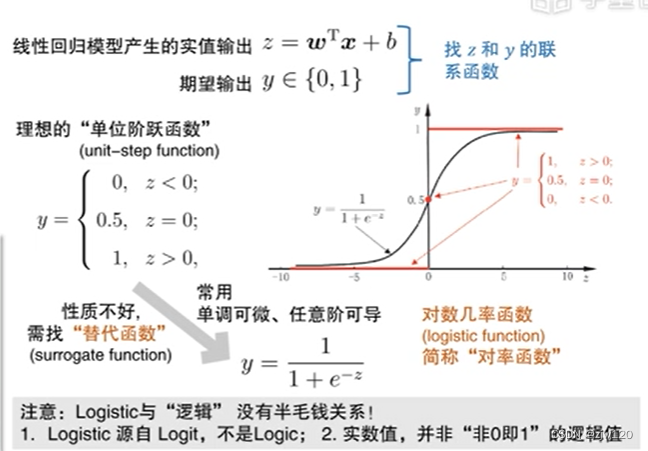
几率:正例的概率/负例的概率
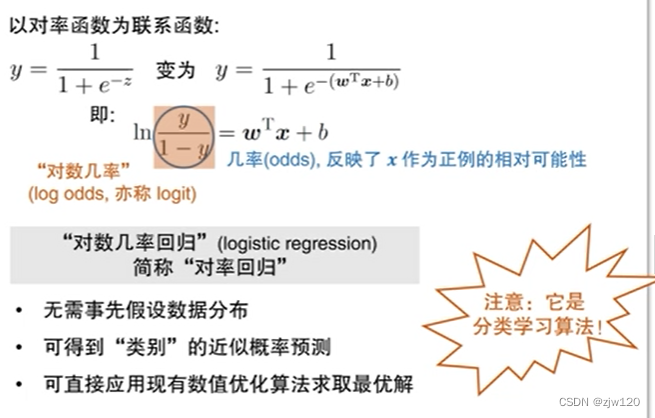
对率回归:针对分类问题,
- 无需实现假设数据分布——没有独立同分布假设
- 可得到“类别”的近似概率预测
- 可直接应用现有的数值优化算法库 求解最优问题
求解步骤
梯度为0是极值点的前提条件是原函数是凸函数,而 ( 1 e − ( w x + b ) − y ) 2 (\frac{1}{e^{-(wx+b)}}-y)^2 (e−(wx+b)1−y)2不是一个凸函数,所以不能直接求导,令等式为0.
正确方法是使用极大似然法。求
m
a
x
p
(
真
正
例
)
p
(
预
测
正
)
+
p
(
真
负
例
)
p
(
预
测
负
)
max p(真正例)p(预测正)+p(真负例)p(预测负)
maxp(真正例)p(预测正)+p(真负例)p(预测负),推导出来的式子是一个高阶可导连续函数,之后通过梯度下降/牛顿法求解梯度等于0的解。

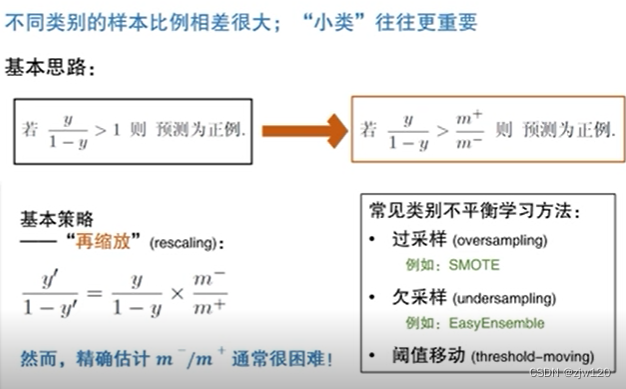
类别不平衡——正负类占总类的比例不一样,不是无偏采样
y
1
−
y
>
1
\frac{y}{1-y}>1
1−yy>1隐含信息就是
y
>
1
/
2
y>1/2
y>1/2,也就是当类别平衡的时候在[0,1]区间大于1/2就判定为正例,小于1/2就判定为负例。
若采样不平衡,就要采用——再缩放,比如用
m
+
m
−
\frac{m^+}{m^-}
m−m+替换1/2,就是采用阈值移动的方法
类别不平衡问题中,当小类比大类重要时,需要做特殊处理。


发表评论