摘要: 图像分割是指把图像分解成各具特性的区域并提取出有用目标的技术, 它是由图像处理到图像分析的一个关键步骤, 已在诸如计算机视觉、图像编码、模式识别和医学图像分析等很多领域有着实际的应用。根据图像自身存在许多不确定性和不精确性,近年来一些学者将模糊聚类应用于图像分割中, 效果要好于传统的图像分割方法。本文首先介绍了硬均值算法hcm和模糊均值fcm算法, 接着介绍了对模糊均值聚类算法的不足之处进行了改进的fcm_s、fcm_s1、fcm_s2和enfcm算法,以及flicm算法,以及他们的实现。针对经典算法的缺点, 在两个方面进行了改进,引入模糊因子,结合局部空间信息和灰度级信息论文把改进的算法应用于图像分割。本文对基于划分的聚类算法的图像分割进行了探讨, 然后局部模糊聚类的角度出发, 得到一种图像分割算法。实验表明这种新的算法具有良好的图像分割效果。
关键词:模糊聚类,图像分割,fcm 灰度级,fcm_s,fcm_s1, fcm_s2,直接邻域,enfcm,flicm,空间信息
目录
1.1 经典fcm (fuzzy c-means algorithm):
1.2 约束模糊聚类fcm_s(fuzzy clustering with constraints):
1.3 约束模糊聚类的变体算法fcm_s1/ fcm_s2:
1.4 加强模糊聚类enfcm (enhanced fuzzy c-means clustering):
1.5 模糊局部信息聚类flicm(fuzzy local information c-means clustering algorithm):
一、理论依据与相关模型
1.1 经典fcm (fuzzy c-means algorithm):
首次提出模糊c -均值(fcm)聚类算法的是dunn,后来由bezdek引申。这是一个迭代算法,仅仅利用了像素点的灰度值信息。

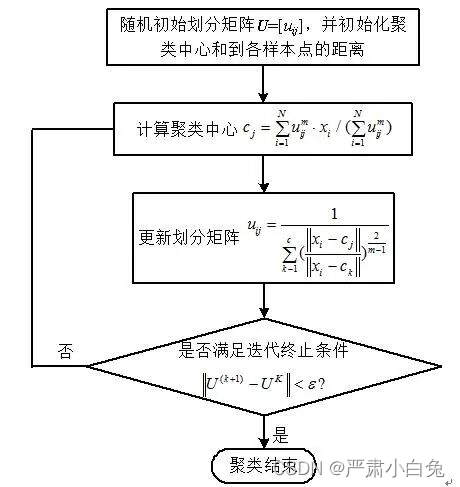
图1.1 fcm算法程序框图
function immm=fcm(im)
%im是输入的源图像
%ix2是分类结果
%im=imread('008.png');
%subplot(2,2,1),imshow(uint8(im)),title('原始图像');
im=im(:,:,1);
%subplot(2,2,2),imshow(uint8(im)),title('灰度图像');
[maxx,maxy]=size(im);%图像大小
%im=imnoise(im,'gaussian',0,0.002);
im=double(im);
imm=cat(3,im,im,im);
%初始化聚类中心(3类)
cc1=8;
cc2=100;
cc3=200;
ttfcm=0;%聚类次数,最多15次
while(ttfcm<15)
ttfcm=ttfcm+1;
c1=repmat(cc1,maxx,maxy);
c2=repmat(cc2,maxx,maxy);
c3=repmat(cc3,maxx,maxy);
c=cat(3,c1,c2,c3);
ree=repmat(0.000001,maxx,maxy);
ree1=cat(3,ree,ree,ree);
distance=imm-c;
distance=distance.*distance+ree1;
daoshu=1./distance;
daoshu2=daoshu(:,:,1)+daoshu(:,:,2)+daoshu(:,:,3);
%计算隶属度u
distance1=distance(:,:,1).*daoshu2;
u1=1./distance1;
distance2=distance(:,:,2).*daoshu2;
u2=1./distance2;
distance3=distance(:,:,3).*daoshu2;
u3=1./distance3;
%计算聚类中心z
ccc1=sum(sum(u1.*u1.*im))/sum(sum(u1.*u1));
ccc2=sum(sum(u2.*u2.*im))/sum(sum(u2.*u2));
ccc3=sum(sum(u3.*u3.*im))/sum(sum(u3.*u3));
tmpmatrix=[abs(cc1-ccc1)/cc1,abs(cc2-ccc2)/cc2,abs(cc3-ccc3)/cc3];
pp=cat(3,u1,u2,u3);
for i=1:maxx;
for j=1:maxy;
if max(pp(i,j,:))==u1(i,j)
ix(i,j)=1;
elseif max(pp(i,j,:))==u2(i,j)
ix2(i,j)=2;
else
ix2(i,j)=3;
end
end
end
%判结束条件
if max(tmpmatrix)<0.0001
break;
else
cc1=ccc1;
cc2=ccc2;
cc3=ccc3;
end
for i=1:maxx;
for j=1:maxy;
if ix2(i,j)==3
immm(i,j)=240;
elseif ix2(i,j)==2
immm(i,j)=20;
else
immm(i,j)=20;
end
end
end
end
for i=1:maxx;
for j=1:maxy;
if ix2(i,j)==3
immm(i,j)=240;
elseif ix2(i,j)==2
immm(i,j)=20;
else
immm(i,j)=20;
end
end
end
%显示最终分类结果
immm=uint8(immm);
%subplot(3,3,4),imshow(immm),
title('fcm聚类结果');
%end1.2 约束模糊聚类fcm_s(fuzzy clustering with constraints):
ahmed等人通过引入直接相邻像素的分类提出了一种fcm标准的修改方法。fcm通过对像素点的8邻域点作用,加入了空间信息,提高了噪声图像的鲁棒性;但也引入了权衡参数a, a值只能通过经验或无数次实验得到实验证明a值对分割结果影响很大。
修改后的目标函数及隶属度,聚类中心更新公式如下:

function immm=fcm_s(im)
%im是输入的源图像
%ix2是分类结果
%im=imread('012.bmp');
%subplot(2,2,1),imshow(uint8(im)),title('原始图像');
im=im(:,:,1);
%subplot(2,2,1),imshow(uint8(im)),title('灰度图像');
[maxx,maxy]=size(im);%图像大小
%im = imnoise(im,'salt & pepper',0.02);
%im=imnoise(im,'gaussian',0,0.002);
im=double(im);
imm=cat(3,im,im,im);
%初始化聚类中心(3类)
cc1=20;
cc2=130;
cc3=240;
ttfcm=0;%聚类次数,最多15次
while(ttfcm<15)
ttfcm=ttfcm+1;
c1=cc1*ones(maxx,maxy);
c2=cc2*ones(maxx,maxy);
c3=cc3*ones(maxx,maxy);
c=cat(3,c1,c2,c3);
a=[1,1,1;1,0,1;1,1,1];
%计算隶属度u
distance=imm-c;
distance=distance.*distance ;%3维矩阵
distance1=distance(:,:,1)+0.125*filter2(a,distance(:,:,1));
distance2=distance(:,:,2)+0.125*filter2(a,distance(:,:,2));
distance3=distance(:,:,3)+0.125*filter2(a,distance(:,:,3));
u1=distance1./(distance1+distance2+distance3);
u2=distance2./(distance1+distance2+distance3);
u3=distance3./(distance1+distance2+distance3);
%计算聚类中心z
im=0.225*filter2(a,im)+im;
%im=256/max(max(im))*im;
%subplot(2,2,3),imshow(uint8(im)),title('变换图像');
ccc1=sum(sum(u1.*u1.*im))/(2.8*sum(sum(u1.*u1)));
ccc2=sum(sum(u2.*u2.*im))/(2.8*sum(sum(u2.*u2)));
ccc3=sum(sum(u3.*u3.*im))/(2.8*sum(sum(u3.*u3)));
tmpmatrix=[abs(cc1-ccc1)/cc1,abs(cc2-ccc2)/cc2,abs(cc3-ccc3)/cc3];
pp=cat(3,u1,u2,u3);
for i=1:maxx;
for j=1:maxy;
if max(pp(i,j,:))==u1(i,j)
ix2(i,j)=1;
elseif max(pp(i,j,:))==u2(i,j)
ix2(i,j)=2;
else
ix2(i,j)=3;
end
end
end
%判结束条件
if max(tmpmatrix)<0.00001
break;
else
cc1=ccc1;
cc2=ccc2;
cc3=ccc3;
end
for i=1:maxx;
for j=1:maxy;
if ix2(i,j)==3
immm(i,j)=0;
elseif ix2(i,j)==2
immm(i,j)=0;
else
immm(i,j)=255;
end
end
end
end
for i=1:maxx;
for j=1:maxy;
if ix2(i,j)==3
immm(i,j)=0;
elseif ix2(i,j)==2
immm(i,j)=0;
else
immm(i,j)=255;
end
end
end
%显示最终分类结果
immm=uint8(immm);
%subplot(1,3,1),imshow(immm),
title('fcm_s聚类结果');
%end1.3 约束模糊聚类的变体算法fcm_s1/ fcm_s2:
fcms 算法的提出使得分割效果有了很大的改善,但由于 fcms 算法在每一次迭代中都需要计算像素的邻域信息,导致fcms 算法的效率非常低下。针对此问题,张道强等人提出了 fcms1 和 fcms2 算法,该种算法是运用均值滤波和中值滤波提前计算出像素的邻域信息,可以保证在分割效果的前提下有效提高算法的效率和鲁棒性。高斯噪声修改后的目标函数及更新公式如下:

function immm=fcms1(im)
%im是输入的源图像
%ix2是分类结果im=imread('012.bmp');
%subplot(2,3,1),imshow(uint8(im)),title('原始图像');
im=im(:,:,1);
%subplot(2,3,2),imshow(uint8(im)),title('灰度图像');
[maxx,maxy]=size(im);%图像大小
%im = imnoise(im,'salt & pepper',0.02);
%im=imnoise(im,'gaussian',0,0.002);
%subplot(2,3,3),imshow(uint8(im)),title('加噪图像');
im=double(im);
a=fspecial('average',3) ;
im= filter2(a,im);%进行中值滤波;
%subplot(2,3,4),imshow(uint8(im)),title('均值滤波图像');
imm=cat(3,im,im,im,im,im,im);
%初始化聚类中心(3类)
cc1=20;
cc2=130;
cc3=240;
ttfcm=0;%聚类次数,最多15次
while(ttfcm<15)
ttfcm=ttfcm+1;
c1=cc1*ones(maxx,maxy);
c2=cc2*ones(maxx,maxy);
c3=cc3*ones(maxx,maxy);
c=cat(3,c1,c2,c3,c1,c2,c3);
%计算隶属度u
distance=imm-c;
distance=distance.*distance ;%3维矩阵
distance1=distance(:,:,1)+1.8*distance(:,:,4);
distance2=distance(:,:,2)+1.8*distance(:,:,5);
distance3=distance(:,:,3)+1.8*distance(:,:,6);
u1=distance1./(distance1+distance2+distance3);
u2=distance2./(distance1+distance2+distance3);
u3=distance3./(distance1+distance2+distance3);
%计算聚类中心c:
ccc1=sum(sum(u1.*u1.*(im+1.8*im)))/(2.8*sum(sum(u1.*u1)));
ccc2=sum(sum(u2.*u2.*(im+1.8*im)))/(2.8*sum(sum(u2.*u2)));
ccc3=sum(sum(u3.*u3.*(im+1.8*im)))/(2.8*sum(sum(u3.*u3)));
tmpmatrix=[abs(cc1-ccc1)/cc1,abs(cc2-ccc2)/cc2,abs(cc3-ccc3)/cc3];
pp=cat(3,u1,u2,u3);
for i=1:maxx;
for j=1:maxy;
if max(pp(i,j,:))==u1(i,j)
ix2(i,j)=1;
elseif max(pp(i,j,:))==u2(i,j)
ix2(i,j)=2;
else
ix2(i,j)=3;
end
end
end
%判结束条件
if max(tmpmatrix)<0.00001
break;
else
cc1=ccc1;
cc2=ccc2;
cc3=ccc3;
end
for i=1:maxx;
for j=1:maxy;
if ix2(i,j)==3
immm(i,j)=0;
elseif ix2(i,j)==2
immm(i,j)=0;
else
immm(i,j)=255;
end
end
end
end
for i=1:maxx;
for j=1:maxy;
if ix2(i,j)==3
immm(i,j)=0;
elseif ix2(i,j)==2
immm(i,j)=0;
else
immm(i,j)=255;
end
end
end
%显示最终分类结果subplot(1,3,2),imshow(immm),
immm=uint8(immm);
title('fcm_s1聚类结果');
%endfunction immm=fcms2(im)
%im是输入的源图像
%ix2是分类结果
%im=imread('012.bmp');
%subplot(2,3,1),imshow(uint8(im)),title('原始图像');
im=im(:,:,1);
%subplot(2,3,2),imshow(uint8(im)),title('灰度图像');
[maxx,maxy]=size(im);%图像大小
%im = imnoise(im,'salt & pepper',0.02);
%im=imnoise(im,'gaussian',0,0.002);
%subplot(2,3,3),imshow(uint8(im)),title('加噪图像');
im=double(im);
im=medfilt2(im,[3,3]);%进行中值滤波;
%subplot(2,3,4),imshow(uint8(im)),title('中值滤波图像');
imm=cat(3,im,im,im,im,im,im);
%初始化聚类中心(3类)
cc1=20;
cc2=130;
cc3=240;
ttfcm=0;%聚类次数,最多15次
while(ttfcm<15)
ttfcm=ttfcm+1;
c1=cc1*ones(maxx,maxy);
c2=cc2*ones(maxx,maxy);
c3=cc3*ones(maxx,maxy);
c=cat(3,c1,c2,c3,c1,c2,c3);
%计算隶属度u
distance=imm-c;
distance=distance.*distance ;%3维矩阵
distance1=distance(:,:,1)+1.8*distance(:,:,4);
distance2=distance(:,:,2)+1.8*distance(:,:,5);
distance3=distance(:,:,3)+1.8*distance(:,:,6);
u1=distance1./(distance1+distance2+distance3);
u2=distance2./(distance1+distance2+distance3);
u3=distance3./(distance1+distance2+distance3);
%计算聚类中心c:
ccc1=sum(sum(u1.*u1.*(im+1.8*im)))/(2.8*sum(sum(u1.*u1)));
ccc2=sum(sum(u2.*u2.*(im+1.8*im)))/(2.8*sum(sum(u2.*u2)));
ccc3=sum(sum(u3.*u3.*(im+1.8*im)))/(2.8*sum(sum(u3.*u3)));
tmpmatrix=[abs(cc1-ccc1)/cc1,abs(cc2-ccc2)/cc2,abs(cc3-ccc3)/cc3];
pp=cat(3,u1,u2,u3);
for i=1:maxx
for j=1:maxy
if max(pp(i,j,:))==u1(i,j)
ix2(i,j)=1;
elseif max(pp(i,j,:))==u2(i,j)
ix2(i,j)=2;
else
ix2(i,j)=3;
end
end
end
%判结束条件
if max(tmpmatrix)<0.00001
break;
else
cc1=ccc1;
cc2=ccc2;
cc3=ccc3;
end
for i=1:maxx
for j=1:maxy
if ix2(i,j)==3
immm(i,j)=0;
elseif ix2(i,j)==2
immm(i,j)=0;
else
immm(i,j)=255;
end
end
end
end
for i=1:maxx;
for j=1:maxy;
if ix2(i,j)==3
immm(i,j)=0;
elseif ix2(i,j)==2
immm(i,j)=0;
else
immm(i,j)=255;
end
end
end
%显示最终分类结果
immm=uint8(immm);
%subplot(1,3,3),imshow(immm),
title('fcm_s2聚类结果');
%end1.4 加强模糊聚类enfcm (enhanced fuzzy c-means clustering):
szilagyi等人提出的enfcm算法加快了灰度图像的聚类过程。通过对像素点及其8邻域像素的线性加权求和预处理原图像,形成了从原始图像到其局部的邻域像素的平均图像。由于像素的灰度级值一般是8位分辨率(256级灰度),m级灰度值的编码一般比像素点大小为n的值小很多。因此,执行时间明显减少。

enfcm提供了与 fcm_s可比的分割结果,但其分割的质量取决于所选择的窗口大小,参数a和过滤方法。如果参数a选择是足够大,该方法抗噪声强。但是,另一方面,当a选择足够小时,可分段图像保持其清晰度和细节。然而,如果没有图像噪声的先验知识,选择参数并不是一件容易的事,只能通过经验或通过反复多次试验得出理想的值。
function immm=enfcm(im)
%im是输入的源图像
%ix2是分类结果im=imread('001.jpg');
%subplot(2,2,1),imshow(uint8(im)),title('原始图像');
im=uint8(im);
im=im(:,:,1);
%subplot(2,2,2),imshow(uint8(im)),title('灰度图像');
[maxx,maxy]=size(im);%图像大小
%im = imnoise(im,'salt & pepper',0.02);
%im=imnoise(im,'gaussian',0,0.002);
im=double(im);
a=[1,1,1;1,0,1;1,1,1];
im=1/2.8 *(0.125* filter2(a,im)+im);%参数a=0.5
%subplot(2,2,3),imshow(uint8(im)),title('变换图像');
imm=cat(3,im,im,im);
%初始化聚类中心(3类)
ttfcm=0;%聚类次数,最多15次
cc1=8;
cc2=120;
cc3=200;
while(ttfcm<15)
ttfcm=ttfcm+1;
c1=cc1*ones(maxx,maxy);
c2=cc2*ones(maxx,maxy);
c3=cc3*ones(maxx,maxy);
c=cat(3,c1,c2,c3);
ree=repmat(0.00001,maxx,maxy);
ree1=cat(3,ree,ree,ree);
distance=imm-c;
distance=distance.*distance+ree1;
%计算隶属度u
distance1=double( distance(:,:,1)+distance(:,:,2)+distance(:,:,3));
u1=distance(:,:,1)./distance1;
u2=distance(:,:,2)./distance1;
u3=distance(:,:,3)./distance1;
%计算聚类中心c
r=zeros(1,256); %创建一个全零矩阵,1×256,计算各灰度出现的次数
for i=1:256
r(i)=length(find(im == (i-1)));
end
im=uint8(im);
uu1=zeros(1,256);
uu2=zeros(1,256);
uu3=zeros(1,256);
for m=1:1:maxx*maxy
uu1(im(m)+1)=u1(m);
uu2(im(m)+1)=u2(m);
uu3(im(m)+1)=u3(m);
end
x=1:1:256;
ccc1=double(sum(r.*x.*uu1.*uu1)/sum(r.*uu1.*uu1));
ccc2=double(sum(r.*x.*uu2.*uu2)/sum(r.*uu2.*uu2));
ccc3=double(sum(r.*x.*uu3.*uu3)/sum(r.*uu3.*uu3));
abs1=abs(cc1-ccc1)/cc1;
abs2=abs(cc2-ccc2)/cc2;
abs3=abs(cc3-ccc3)/cc3;
tmpmatrix=[abs1,abs2,abs3];
pp=cat(3,u1,u2,u3);
for i=1:maxx
for j=1:maxy
max1=max([pp(i,j,1),pp(i,j,2),pp(i,j,3)]);
if max(max1)==u1(i,j)
ix2(i,j)=1;
elseif max(max1)==u2(i,j)
ix2(i,j)=2;
else
ix2(i,j)=3;
end
end
end
%判结束条件
if max(tmpmatrix)<0.000000001
break;
else
cc1=ccc1;
cc2=ccc2;
cc3=ccc3;
end
for i=1:maxx
for j=1:maxy
if ix2(i,j)==3
immm(i,j)=20;
elseif ix2(i,j)==2
immm(i,j)=255;
else
immm(i,j)=255;
end
end
end
end
for i=1:maxx
for j=1:maxy
if ix2(i,j)==3
immm(i,j)=20;
elseif ix2(i,j)==2
immm(i,j)=255;
else
immm(i,j)=255;
end
end
end
%显示最终分类结果subplot(1,2,1),imshow(immm),
immm=uint8(immm);
title('enfcm聚类结果');1.5 模糊局部信息聚类flicm(fuzzy local information c-means clustering algorithm):
stelios krinidis和vassilios提出了一种改进的模糊c -均值的聚类(fcm)算法,用于图像的聚类分割。改进算法结合局部空间信息和灰度级信息,是一种新型的模糊方式,被称为模糊局部信息c -均值(flicm)。 2010年4月发表在ieee上。
fli cm定义了有如下特性的模糊因子:
(1)包括空间信息和灰度级信息,提高鲁棒性和噪声灵敏性
(2)以邻域像素到中心像素的距离,控制其影响
(3)使用原始图像,避免预处理可能会导致细节丢失
(4)无任何参数的选择

该算法对噪声容限和离散抗阻性能,完全依靠新的模糊因子,因为是自动确定,而不是人为设置的。即使在没有任何先验的噪声知识的情况下,该值将自动在每次迭代中重新计算,汇聚成中央像素的值从而保持噪声和离散的不灵敏性。
function immm = flicm(im)
%function [ix2]=flicm(im);
%im是输入的源图像
%ix2是分类结果
%im=imread(im);
%figure(1)
%subplot(2,2,1),imshow(uint8(im)),title('原始图像');
im=im(:,:,1);
%subplot(2,2,2),imshow(uint8(im)),title('灰度图像');
[maxx,maxy]=size(im);%图像大小
%im = imnoise(im,'salt & pepper',0.02);
%im=imnoise(im,'gaussian',0,0.002);
im=double(im);
imm=cat(3,im,im,im);
%初始化聚类中心(3类)
cc1=8;
cc2=100;
cc3=200;
ttfcm=0;%聚类次数,最多15次
a=[1,1,1;1,0,1;1,1,1];
b=ones(maxx,maxy);
ggg1=80*rand(maxx,maxy);
ggg2=80*rand(maxx,maxy);
ggg3=80*rand(maxx,maxy);
g=cat(3,ggg1,ggg2,ggg3);
while(ttfcm<15)
ttfcm=ttfcm+1;
c1=repmat(cc1,maxx,maxy); %产生一个全cc1的m*n的矩阵
c2=repmat(cc2,maxx,maxy);
c3=repmat(cc3,maxx,maxy);
c=cat(3,c1,c2,c3); %聚类中心矩阵
ree=repmat(0.001,maxx,maxy);
ree1=cat(3,ree,ree,ree);
distance0=imm-c; %d=每一个像素点和聚类中心的距离
distance=distance0.*distance0+ree1+g;
%计算每个像素点属于各类的隶属度u
daoshu=1./distance;
daoshu2=daoshu(:,:,1)+daoshu(:,:,2)+daoshu(:,:,3);
distance1=distance(:,:,1).*daoshu2;
u1=1./distance1;
distance2=distance(:,:,2).*daoshu2;
u2=1./distance2;
distance3=distance(:,:,3).*daoshu2;
u3=1./distance3;
%计算模糊算子
gg1=(b-u1).*(b-u1).*distance(:,:,1);
g1=0.5*imfilter(gg1,a);
gg2=(b-u1).*(b-u2).*distance(:,:,2);
g2=0.5*imfilter(gg2,a);
gg3=(b-u1).*(b-u3).*distance(:,:,3);
g3=0.5*imfilter(gg3,a);
g=cat(3,g1,g2,g3);
%计算聚类中心c
ccc1=sum(sum(u1.*u1.*im))/sum(sum(u1.*u1));
ccc2=sum(sum(u2.*u2.*im))/sum(sum(u2.*u2));
ccc3=sum(sum(u3.*u3.*im))/sum(sum(u3.*u3));
tmpmatrix=[abs(cc1-ccc1)/cc1,abs(cc2-ccc2)/cc2,abs(cc3-ccc3)/cc3];
pp=cat(3,u1,u2,u3);%隶属度矩阵
for i=1:maxx
for j=1:maxy
if max(pp(i,j,:))==u1(i,j)
ix2(i,j)=1;
elseif max(pp(i,j,:))==u2(i,j)
ix2(i,j)=2;
else
ix2(i,j)=3;
end
end
end
%判结束条件
if max(tmpmatrix)<0.0001
break;
else
cc1=ccc1;
cc2=ccc2;
cc3=ccc3;
end
for i=1:maxx
for j=1:maxy
if ix2(i,j)==3
immm(i,j)=240;
elseif ix2(i,j)==2
immm(i,j)=0;
else
immm(i,j)=0;
end
end
end
%显示每次聚类分割结果
%subplot(2,2,3),imshow(uint8(immm)),title('第3次聚类结果');
end
for i=1:maxx
for j=1:maxy
if ix2(i,j)==3
immm(i,j)=240;
elseif ix2(i,j)==2
immm(i,j)=0;
else
immm(i,j)= 0;
end
end
end
%显示最终分类结果
immm=uint8(immm);
%axes(handles.axes5);
%subplot(1,2,2),
%imshow(immm),title('flicm聚类结果');
end1.6 fcm系列算法综述与对比
fcm算法是一种基于划分的聚类算法,它的思想就是使得被划分到同一簇的对象之间相似度最大,而不同簇之间的相似度最小。它是k-means聚类的一种延伸。k-means也叫硬c均值聚类(hcm),而fcm是模糊c均值聚类,hcm与fcm最大的区别在于隶属函数(划分矩阵)的取值不同,hcm的隶属函数只取两个值:0和1,而fcm的隶属函数可以取[0,1]之间的任何数。k-means和fcm都需要事先给定聚类的类别数,而fcm还需要选取恰当的加权指数α,α的选取对结果有一定的影响,α属于[0,+∞)。
fcm_s对经典fcm的目标函数进行了修改,以补偿强度的不均匀性,并允许像素的标记受到其紧邻像素的影响。 fcm_s的一个缺点是在每个迭代步骤中都要计算邻域标签,这非常耗时。而fcm_s1和fcm_s2为了减少计算时间分别引入了额外的均值和中值滤波图像,这些图像可以预先计算,以代替fcm_s的邻域项。因此,fcm_s1和fcm_s2的执行时间都大大减少了。
enfcm的结构不同于fcm_s及其变体。 首先,由原始图像和每个像素的局部邻域平均灰度级形成线性加权和图像。 然后,基于灰度直方图而不是求和图像的像素执行聚类。 由于图像中的灰度级数通常比其像素数小得多,因此减少了enfcm算法的计算时间,而分割后的图像的质量与fcm_s几乎一致。
flicm是一种新颖的鲁棒的模糊局部信息聚类算法,该算法可以处理参数α选择的缺陷,并提高图像分割性能。在flicm中,定义了一种新颖的模糊因子来替换enfcm和fcm s及其变体中使用的参数α。新的模糊局部邻域因子可以自动确定空间和灰度关系,并且完全不需要任何参数选择。
二、实验结果总结
2.1 主观评价(效果图对比)
fcm只是对每一个像素点的灰度值作用,故噪声对分割影响较大;fcm_s加入了对紧邻像素的考虑,其变体1,2通过对像素点的邻域求和均值中值化,对图像进行了滤波预处理,受噪声影响相对较小


图2.1原图(左)与fcm(右)
由于均值滤波和中值滤波可以较好地抑制高斯噪声和椒盐噪声的影响,因而 fcm_s1 算法和 fcm_s2 算法可以获得比 fcm 算法更好的分割结果从所示的实验结果可以看出,fcm_s1 算法和 fcm_s2 算法同fcms 算法一样,其分割结果都比较接近理想的分割结果,而这两种变体的运行效率则远胜fcms。



图2.2 fcm_s(左)、fcm_s1(中)与fcm_s2(右)
仔细比较 fcms 算法、fcm_s1 算法和 fcm_s2 算法,可以发现:三种算法的分割结果不相上下,而fcm_s1 算法和 fcm_s2 算法的运行效率比 fcms 算法略胜一筹。
enfcm通过线性加权对图像进行了预处理,运行效率较高,效果与fcms几乎一致;

图2.3 enfcm算法
上述改进的 fcm 算法获得了相比原 fcm 算法更好的分割结果,但是所考虑的邻域像素对中心像素影响并不准确,即邻域内所有像素对中心像素的影响程度一样,均由参数决定,致使分割结果并不是很理想。上述改进的 fcm 算法在图像中边界处的分割并不准确。
总而言之,尽管上述模糊聚类改进算法有较好的分割效果,但是他们仍有许多不足之处:
(1)对噪声和离值缺乏鲁棒性;
(2)参数选择难,需要反复试验来确定最佳参数;
(3)预先对图像进行滤波处理,会导致丢失图像细节。
flicm算法解决了上述问题,首先,利用 gij(模糊因子)不包含除必要参数m、c 之外的其它参数,因此无需通过调整参数(例如 enfcm 算法中的c)来平衡
图像噪声和图像细节,并且,该算法能够利用空间信息和灰度信息,相对于传统的fcm 算法,对于含有噪声的图像,分割效果有了极大的改善。
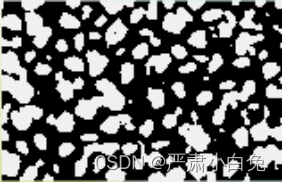
图2.4 flicm算法
2.2 客观评价(经典评价指数)
fcm广泛应用于数据聚类和图像分割领域,如何判定该算法的优劣性,是评价数据分类好坏和分割技术高低的关键。其中有几种经典的评价指数:

图2.5评价指数对应含义
具体数值上:bezdek划分系数bezdek_v 越大越好,xie_beni系数xie_beni_v和重构错误率v_re越小越好。图片选择与处理过程同4.1,经过编程计算,
fcm的bezdek_v , xie_beni_v , v_re指数分别为9.8529e+04,2.0236e+09,1.5668e-28。fcms的bezdek_v , xie_beni_v , v_re指数分别为4.1266e+04,8.1853e+08,1.9594e-28。fcm_s1的bezdek_v , xie_beni_v , v_re指数分别为7.7576e+04,1.7790e+09 ,2.4023e-28。fcm_s2的bezdek_v , xie_beni_v , v_re指数分别为 7.7445e+04,1.8006e+09,2.7378e-28。enfcm的bezdek_v , xie_beni_v , v_re指数分别为7.6878e+04,9.1414e+08,1.1463e-28。flicm的bezdek_v , xie_beni_v , v_re指数分别为1.1685e+05,2.3636e+09,1.0644e-28。如下表
|
| fcm | fcms | fcm_s1 | fcm_s2 | enfcm | flicm |
| bezdek_v | 9.8529 e+04 | 4.1266 e+04 | 7.7576 e+04 | 7.7445 e+04 | 7.6878 e+04 | 1.1685 e+05 |
| xie_beni | 2.0236 e+09 | 8.1853 e+08 | 1.7790 e+09 | 1.8006 e+09 | 9.1414 e+08 | 2.3636 e+09 |
| v_re | 1.5668 e-28 | 1.9594 e-28 | 2.4023 e-28 | 2.7378 e-28 | 1.1463 e-28 | 1.0644 e-28 |
表2.1 三种评价指数具体数值
从bezdek划分系数bezdek_v出发,flicm效果最理想。
从xie_beni系数xie_beni_v出发,flicm效果最理想。
从重构错误率v_re出发,fcm_s2效果最理想。
function [ bezdek_v , xie_beni_v , v_re ] = evaluation_index( u,i,v )
% evaluation_index函数是为了判定分割评价指数
% 输出:bezdek划分系数bezdek_v、xie_beni系数xie_beni_v 和重构错误率v_re构成。
% 输入:隶属度矩阵u、聚类中心v和原始灰度图像矩阵i。
% bezdek划分系数bezdek_v 越大越好
% xie_beni系数xie_beni_v和重构错误率v_re越小越好
bezdek_v=0;
xie_beni_v=0;
v_re=0;
[m,n,c]=size(u);
i_re=zeros(m,n);
min_v=(v(1)-v(2))^2;
for x=1:c
for y=1:c
if(x-y~=0&&min_v>(v(x)-v(y))^2)
min_v=(v(x)-v(y))^2;
end
end
end
for x=1:m
for y=1:n
temp=0;
temp1=0;
for k=1:c
bezdek_v=bezdek_v+ u(x,y,k)^2;
xie_beni_v=xie_beni_v+u(x,y,k)^2*(i(x,y)-v(k))^2;
temp=temp+u(x,y,k)^2*i(x,y);
temp1=temp1+u(x,y,k)^2;
end
i_re(x,y)=temp/temp1;
end
end
for x=1:m
for y=1:n
v_re=v_re+(i_re(x,y)-i(x,y))^2;
end
end
v_re=v_re/m/n;
end



发表评论