【论文笔记】Dynamic Occupancy Grids for Object Detection: A Radar-Centric Approach

原文链接：https://arxiv.org/abs/2402.01488

i. 引言

感知环境在自动驾驶中非常重要，但传统的方法将这一过程分为两方面：动态物体的检测和跟踪，以及使用占用网格表达静态环境。占用网格难以表达高度动态的物体，因此动态占用网格（dogm）的概念被提出，并与粒子滤波器结合，跟踪环境中的静态和动态物体。但是目前的方法多依赖激光雷达，仅使用雷达进行性能提升。随着雷达分辨率的提高，基于雷达的dogm也得到了发展，但只在短期场景中测试，且相比激光雷达方法的改动较少，没有针对雷达的优势进行改进或处理雷达的缺陷。

iii. 方法

a. 环境表达

自车周围的环境被表达为以自车为中心的网格地图，每个网格存储了4种状态（空、静态、动态、未知）的概率。粒子用于帮助跟踪动态占用。每个粒子基于其位置，与特定网格关联。如下图所示。

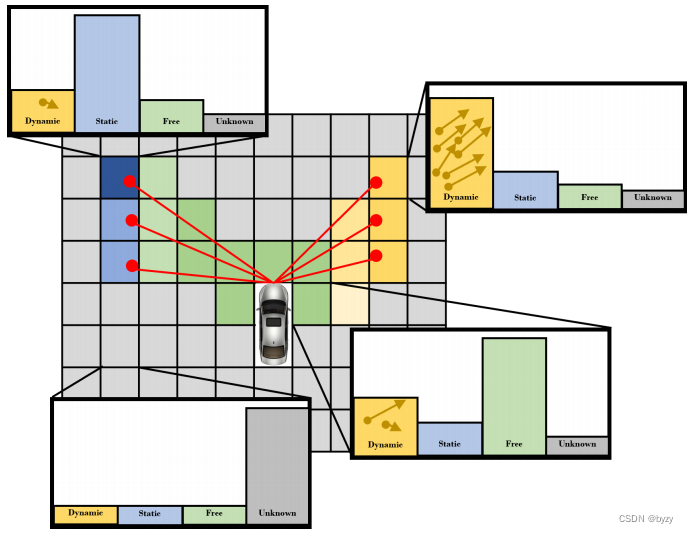
b. 以雷达为中心的动态占用网格建图

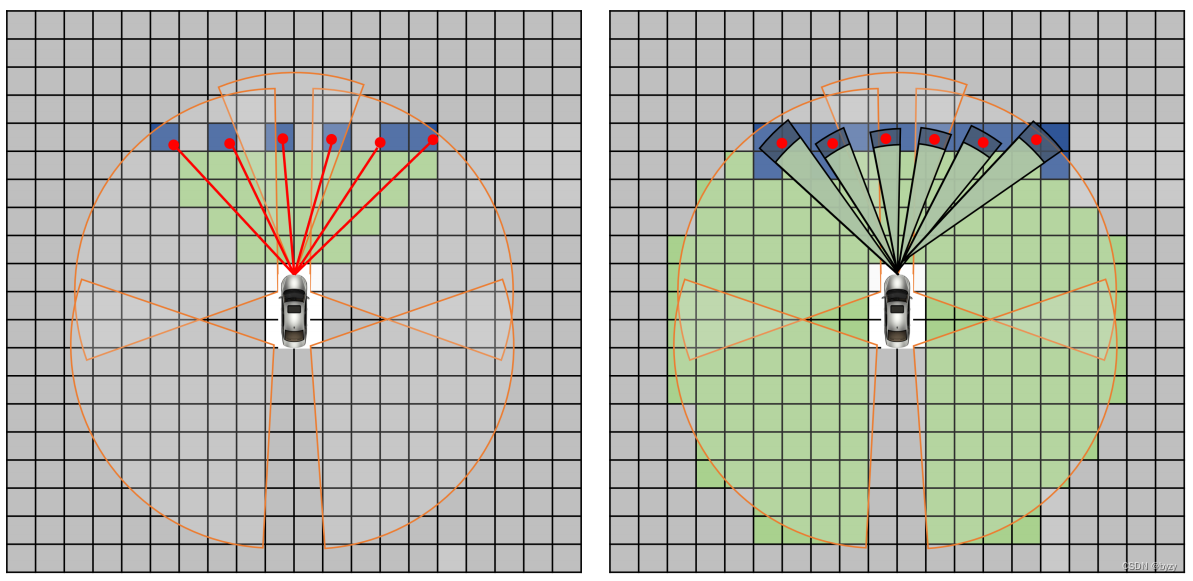
1) 确定测量网格

首先确定由最新的测量影响的网格（占用、空、未知），这需要使用逆传感器模型（ism）。对激光雷达来说，标准的解决方案是使用射线投射算法（如下左图所示）。但雷达的角度不确定性更大，且能在不同程度上穿透材料。此外，雷达的测量比激光雷达少得多，导致跟踪射线无法填充所有的已知空白区域。本文使用考虑角度不确定性和波传播的ism（如下右图所示）。

2) 网格状态计算

基本的假设是，所有未被占用的网格为静态的。

雷达的测量包括位置坐标，自车运动补偿的距离变化率，和rcs值：
$$x_{meas}=[x_{map},y_{map},v_r,rcs{]}^t$$

占用网格或空网格属于空空间的概率$p_{free}$基于与测量之间的距离$d$计算：
$$\begin{gathered} d_c=\Vert [x_{map},y_{map}{]}^t-[x_c,y_c{]}^t{\Vert }_2 \\ {f}_d(d)=\frac{1}{{\sigma }_f\sqrt{2\pi }}\exp (\frac{1}{2}(\frac{d-{\mu }_f}{{\sigma }_f}{)}^2) \\ {p}_{free}=1-f_d(d_c) \end{gathered}$$

属于未知状态的概率$p_{unk}$的计算过程与上述类似，但仅针对未知网格计算。

与激光雷达方法使用网格内粒子的平均速度不同，本文使用测量的距离变化率$v_r$来确定占用网格的动静属性。为确定静态与动态概率，假定非零的距离变化率可表明物体运动。尽管该假设并不总是成立，但不成立的情况很少出现。因此，可通过此区分静态网格。这样，可以减少需要的粒子数，从而减少计算时间（见后文）。对于占用网格，静态和动态的概率按下式计算：
$$\begin{gathered} p_{dyn}=f_d(d)\times p(v_r\ne 0)+(1-f_d(d))\times prior(dyn) \\ {p}_{static}=f_d(d)\times p(v_r=0)+(1-f_d(d))\times prior(static) \end{gathered}$$

其中，距离函数用于减少测量随距离增加的影响。使用归一化rcs值对雷达测量的贡献进行加权：
$$rc{s}_{norm}=\frac{rcs-\min (rcs)}{\max (rcs)-\min (rcs)}$$

可按下式得到各状态概率：
p ∗ = r c s n o r m × p ∗ + ( 1 − r c s n o r m ) × 0.5 ,     ∗ ∈ { u n k , f r e e , s t a t i c , d y n } p_{*}=rcs_{norm}\times p_*+(1-rcs_{norm})\times0.5,\ \ \ *\in\{unk,free,static,dyn\} p∗​=rcsnorm​×p∗​+(1−rcsnorm​)×0.5,   ∗∈{unk,free,static,dyn}

最后，使用贝叶斯公式更新网格的概率。

3) 状态修正

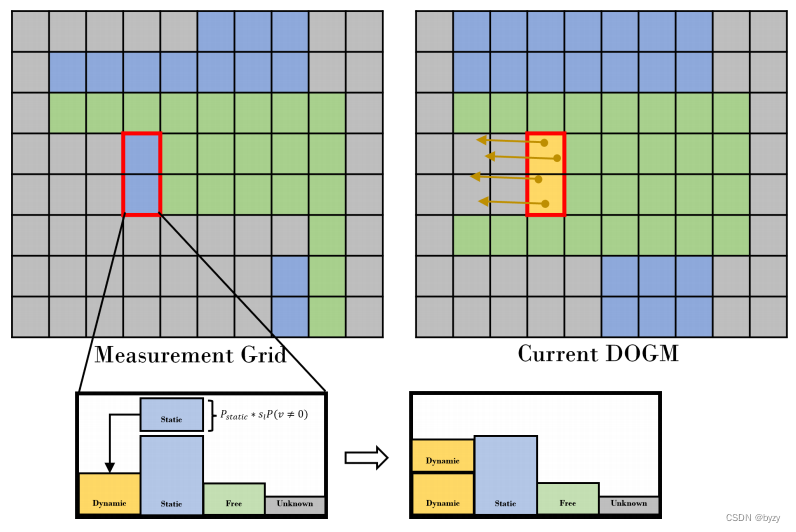
由于运动物体的距离变化率不一定不为0，本文提出两种方法修正网格状态。

测量网格修正：基于“高度动态的网格不能突变为静态”的假设。本文基于已有的积累dogm更新测量网格：
p c = [ p u n k , p f r e e , p s t a t i c , p d y n ] t p c o r r , c = [ 1 0 0 0 0 1 0 0 0 0 1 − s l p ( v ≠ 0 ) d l p ( v = 0 ) 0 0 s l p ( v ≠ 0 ) 1 − d l p ( v = 0 ) ] p c p_c=[p_{unk},p_{free},p_{static},p_{dyn}]^t\\ p_{corr,c}=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1-s_lp(v\neq0)&d_lp(v=0)\\0&0&s_lp(v\neq0)&1-d_lp(v=0)\end{bmatrix}p_c pc​=[punk​,pfree​,pstatic​,pdyn​]tpcorr,c​= ​1000​0100​001−sl​p(v=0)sl​p(v=0)​00dl​p(v=0)1−dl​p(v=0)​ ​pc​

其中$p(v\ne 0)$与$p(v=0)$根据dogm中的平均粒子速度计算，$s_l$与$d_l$位于0到1之间，决定最新测量和现有dogm的权重。

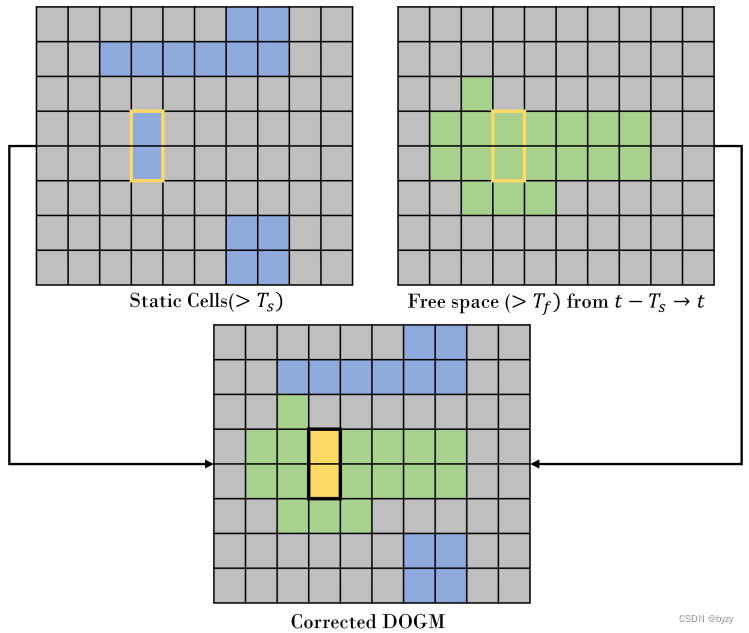
错误的静态检测：为避免将低速动态物体检测为静态物体，本文使用dynablox算法。本文使用网格被分类为静态或空空间的次数来确定其是否为动态物体。若一个网格超过$t_{static}$次被分类为静态，且在过去超过$t_{free}$次被分类为空空间，则将其转化为动态状态。阈值次数用于调节敏感度。

4) 粒子创建、权重计算和重采样

确定每个网格的状态概率后，会对新的动态网格（动态状态的概率最高的网格）创建粒子，与现有的粒子一起组成粒子池。粒子由状态向量${\mathbf{x}}_{\mathbf{p}}=[x_p,y_p,v_x,v_y,w_t{]}^t$表达，其速度被定义在全局坐标系下，而位置被定义在网格坐标系下。权重表达粒子代表被跟踪物体的可能性，由测量决定：
$$w_t=\underset{更新}{f_d(d_p)f_r(r_p)}\underset{先验}{(1-f_d(d_p))(1-ϵ)w_{t-1}}$$

其中$d_p$为粒子与最近测量的距离（即基于距离减弱测量对粒子的影响），$f_r(r_p)$为概率密度函数，用于比较粒子的距离变化率$r_p$和测量的距离变化率。

此外，采样粒子会有与最近测量的距离变化率相匹配的速度，且该速度会被限制在最大速度以下，从而减小距离范围。最后，基于权重重采样粒子。

5) 归一化与占用预测

所有状态概率和粒子权重会被归一化，得到精确的概率。此外，动态状态概率按权重比例在网格内的粒子权重间分布。

最后，所有粒子根据线性运动模型，预测下一时刻的动态占用。使用的状态转移矩阵如下：
[ 1 0.1 0.1 0.05 0 0.9 0 0 0 0 1 − p ( v ≠ 0 ) p ( v = 0 ) 0 0 p ( v ≠ 0 ) 1 − p ( v = 0 ) ] \begin{bmatrix}1&0.1&0.1&0.05\\0&0.9&0&0\\0&0&1-p(v\neq0)&p(v=0)\\0&0&p(v\neq0)&1-p(v=0)\end{bmatrix} ​1000​0.10.900​0.101−p(v=0)p(v=0)​0.050p(v=0)1−p(v=0)​ ​

iv. 评估

a. 评估数据

可通过使用hdbscan算法聚类粒子生成动态物体。

b. 定性评估

可视化表明，本文方法比hsbof-rs有更高的召回率（能避免动态物体的漏检）。但因为聚类算法和雷达dynablox算法的不完美，以及粒子数较少，导致了较低的精度。

跟踪方面，基准方案会在物体垂直于其相对雷达的方向运动时丢失物体，而本文方法因其修正算法不会出现这一现象。

c. 定量评估

在radarscenes数据集上进行动态目标检测任务（使用算法生成边界框），总体来说本文方法不如基于深度学习的方法，但部分指标能达到相当水平，且本文方法能提供的不仅仅是动态目标检测结果。但与hsbof-rs相比，本文方法性能更优。

本文方法在大型车辆上的检测分数最低，这是因为大型物体在雷达测量中通常是支离破碎的。

本文方法的精度比召回率更低。可通过改进聚类算法并微调雷达dynablox来减少假阳性，从而提高精度；可通过整合基于粒子分类的方法，进行更敏感的动态分类，从而提高召回率（在dogm中，召回率低不是因为目标缺失，而是因为网格被错误分类为静态）。