模型预测控制(mpc)简介及matlab实现
基本概念
全称:model-based predictive control(mpc)—模型预测控制
本质:mpc利用一个已有的模型、系统当前的状态和未来的控制量,来预测系统未来的输出,然后与我们期望的系统输出做比较,得到代价函数,通过优化的方法,优化出未来控制量,使得代价函数最小。优化出来的控制量即算法的输出。

核心思想:以优化方法求解最优控制器,其中优化方法大多时候采用二次规划(quadratic programming)
控制输出:mpc控制器优化得到的控制输出也是系统在未来有限时间步的控制序列。 当然,由于理论构建的模型与系统真实模型都有误差,所以,实际上更远未来的控制输出对系统控制的价值很低,故mpc仅执行输出序列中的第一个控制输出。
模型分类:
- 机理模型
- 基于数据的模型,例如用神经网络训练一个modle,使用基于数据的模型的mpc可以结合model based rl使用
预测:根据已有模型,已经未来有限时间步的控制序列,预测出未来的系统状态
控制:优化的控制量,是一个未来有限时间步的控制序列
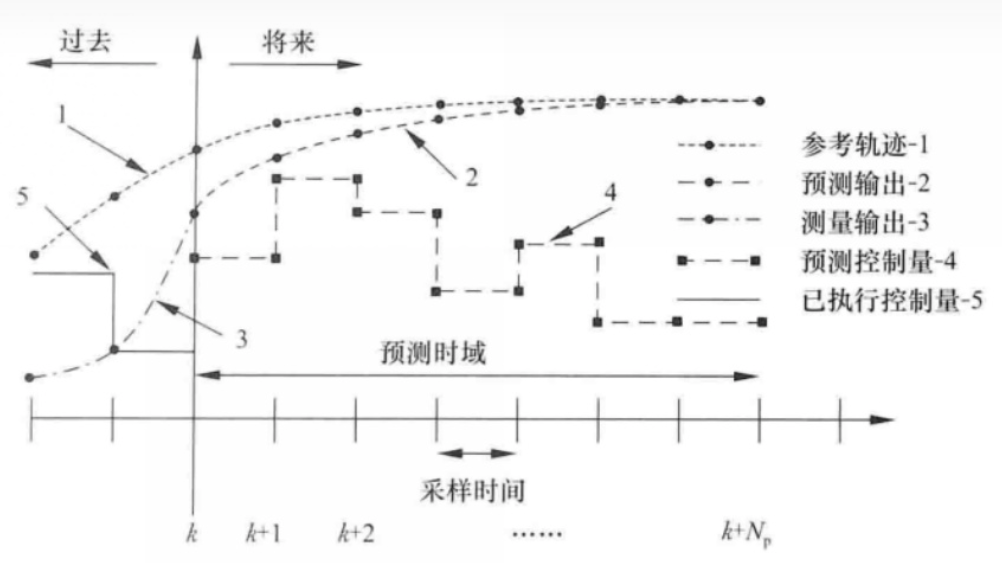
预测区间(predictive horizon):
对于一般的离散化系统,在k时刻,我们可以测量出系统的当前状态y(k),再通过优化计算得到u(k),u(k+1),u(k+2),u(k+j),根据模型与控制量,得到系统未来状态的估计值y(k),y(k+1),y(k+2),y(k+j)。
其中系统未来状态的估计值y(k),y(k+1),y(k+2),y(k+j)这部分就称为预测区间的系统预测值,指的是一次优化后预测未来输出的时间步的个数
控制区间(control horizon)
将控制估计的部分称为控制区间,通过优化计算得到u(k),u(k+1),u(k+2),u(k+j)这部分就称为控制区间的控制量,
在得到最优输入之后,我们只施加当前时刻的输入u(k),即控制区间的第一位控制输入
区间参数配置:
过小的控制区间,可能无法做到较好的控制,而较大的控制区间,比如与预测区间相等,则会导致只有前一部分的控制范围才会有较好的效果,而后一部分的控制范围则收效甚微,而且将带来大量的计算开销。
约束:对于约束,一般分为:
- hard约束:物理性质的约束,不可以违背,例如方向盘的转向,刹车的深度
- soft约束:软件约束,可以违反,例如最大的速度
mpc 优点:
- 善于处理多输入多输出系统(mimo)
- 可以处理约束,如安全性约束,上下阈值
- 是一种向前考虑未来时间步的有限时域优化方法(一定的预测能力)
控制框图:
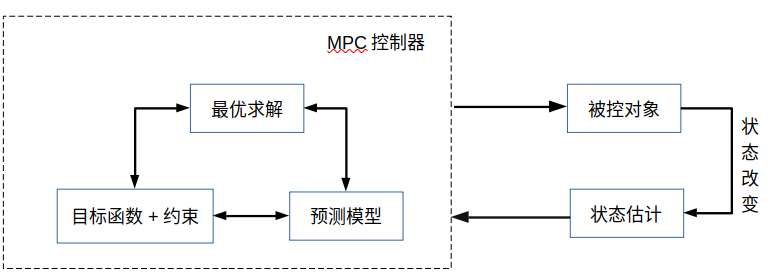
mpc算法 整体流程
模型预测控制在k时刻共需三步
-
第一步:获取系统的当前状态;
-
第二步:基于u(k),u(k+1),u(k+2),u(k+j)进行最优化处理,代价函数为
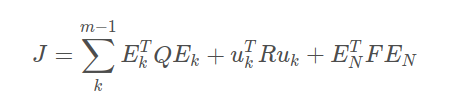
其中en 表示误差的终值,也是衡量优劣的一种标准。 -
第三步:只取u ( k )作为控制输入施加在系统上。
在下一时刻重复以上三步,在下一步进行预测时使用的就是下一步的状态值,我们将这样的方案称为滚动优化控制(receding horizon control)。
数学建模
线性模型
当模型是线性的时候,mpc的设计求解一般使用二次规划方法。
设线性模型为以下形式:
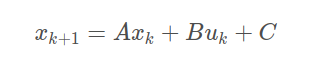
假定未来m步的控制输入已知u(k),u(k+1),u(k+2),u(k+m),根据以上模型与输入,我们可以计算未来m步的状态:
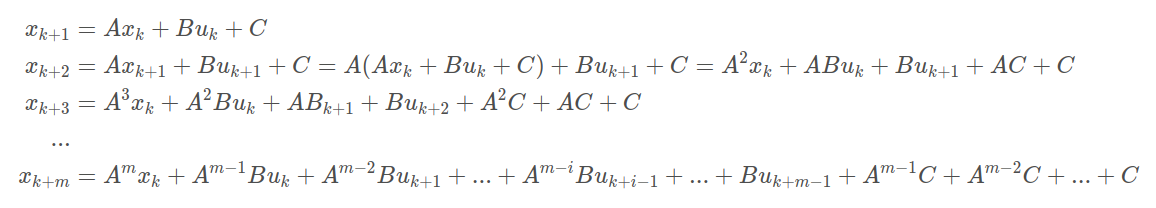
将上面m步写成矩阵向量形式:
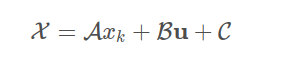
其中,
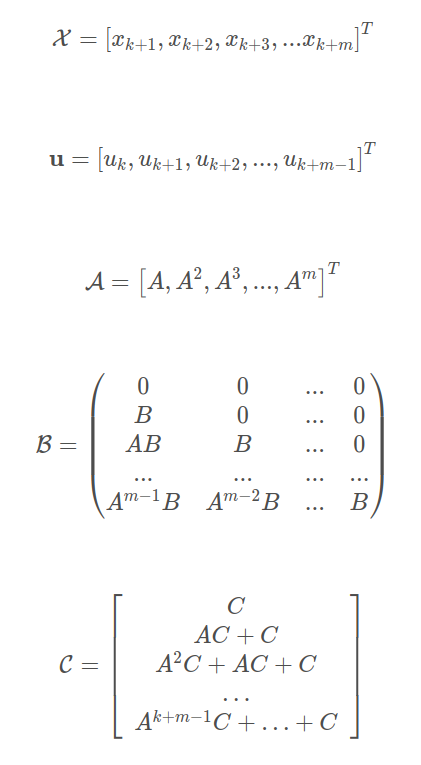
上式b中的下三角形式,直接反映了系统在时间上的因果关系,即k + 1时刻的输入对k 时刻的输出没有影响,k+2时刻的输入对k和k+1时刻没有影响。
假定参考轨迹为
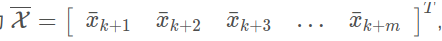
则mpc的一个简单的目标代价函数如下:
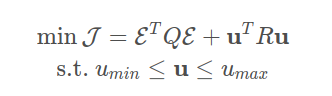
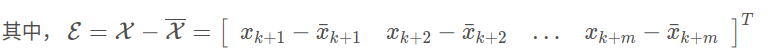
utru 这一项是为了让控制输入不会太大,因此代价函数中添加了一项对控制量的约束。
将状态方程带入代价函数,变量仅剩u,以上最优化问题可用二次规划方法求解,得到满足目标代价函数的最优控制序列
mpc与pid的区别
- pid控制器不具有“前瞻性”:参与计算的各个量,有当前的 ,上个控制周期的 ,以及之前所有的 累计和,没有未来的 。
- pid属于无模型控制。pid仅仅通过目标和当前状态的差距,以及三个控制参数,就输出控制量
matlab实现mpc函数
function [m,c,q_bar,r_bar,g,e,h,u_k] = mpc_zero_ref(a,b,n,x_k,q,r,f)
%%%%%%%%%%%建立一个以0为参考目标的mpc求解函数
%%%%%%%%%%%其中,状态矩阵a,输入矩阵b系统维度n,初始条件x_k,权重矩阵q,r及终端误差矩阵f为输入
%%%%%%%%%%%输出中u_k为所求控制器,其余为简化过程中引入的中间变量
n=size(a,1); %a是n×n矩阵,求n
p=size(b,2); %b是n×p矩阵,求p
m=[eye(n);zeros(n*n,n)];%初始化m矩阵,m矩阵是(n+1)n × n的,
%它上面是n × n个“i”,这一步先把下半部分写成0
c=zeros((n+1)*n,n*p);%初始化c矩阵,这一步令它有(n+1)n × np个0
%定义m和c
tmp=eye(n);%定义一个n × n的i矩阵
for i=1:n%循环,i从1到n
rows = i*n+(1:n);%定义当前行数,从i×n开始,共n行
c(rows,:)=[tmp*b,c(rows-n,1:end-p)];%将c矩阵填满
tmp=a*tmp;%每一次将tmp左乘一次a
m(rows,:)=tmp;%将m矩阵写满
end
%定义q_bar
s_q=size(q,1);%找到q的维度
s_r=size(r,1);%找到r的维度
q_bar=zeros((n+1)*s_q,(n+1)*s_q);%初始化q_bar为全0矩阵
for i=0:n
q_bar(i*s_q+1:(i+1)*s_q,i*s_q+1:(i+1)*s_q)=q;%将q写到q_bar的对角线上
end
q_bar(n*s_q+1:(n+1)*s_q,n*s_q+1:(n+1)*s_q)=f;%将f放在最后一个位置
%定义r_bar
r_bar=zeros(n*s_r,n*s_r);%初始化r_bar为全0矩阵
for i=0:n-1
r_bar(i*s_r+1:(i+1)*s_r,i*s_r+1:(i+1)*s_r)=r;
end
%求解
g=m'*q_bar*m;%g
e=c'*q_bar*m;%e
h=c'*q_bar*c+r_bar;%h
%最优化
f=(x_k'*e')';%定义f矩阵
u_k=quadprog(h,f);%用二次规划求解最优化u_k
end




发表评论