
✨ 慢品人间烟火色,闲观万事岁月长 🌏
📃个人主页:
🔥个人专栏:c++学习
🚀 欢迎关注:👍点赞 👂🏽留言 😍收藏 💞 💞 💞

1. 红黑树的概念
📙红黑树由rudolf bayer在1972年发明,最初被称为平衡二叉b树(symmetric binary b-trees),后来被guibas和robert sedgewick修改为如今的“红黑树”。
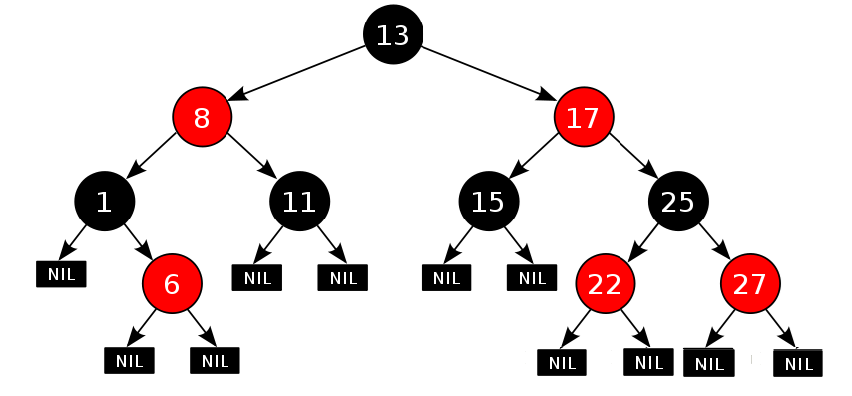
2. 红黑树的性质
3. 红黑树的节点结构及定义
红黑树节点的定义通常包含以下几个关键部分:
🧩3.1 基本元素
🧩3.2 节点颜色(_col)
🧩3.3 构造函数
🧩3.4 br节点定义:
template<class k, class v>
struct bstreenode
{
bstreenode<k, v>* _left; //左子树
bstreenode<k, v>* _right; //右子树
bstreenode<k, v>* _parent; //父亲
pair<k, v> _kv; //存放节点值的
string _col; //颜色(通过这个可以直到左右子树存在情况)
//构造函数
bstreenode(const pair<k, v>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _col("red") //默认颜色为红色
{}
};
红黑树的节点结构与二叉搜索树和avl树差别不大,最大的差别就是加入了一个新的存储点——颜色
4. 红黑树的插入
🌈红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
在我们进行插入操作之前,我们先定义一个红黑树的类
红黑树定义:
template<class k, class v>
class rbttree
{
typedef bstreenode<k, v> node;
public:
// 其他未实现的成员函数
private:
node* _root = nullptr;
};
红黑树的插入操作类似于我们之前avl树的插入,只不过红黑树的插入操作涉及到旋转操作以及考虑其他节点的颜色,前面的操作还是一样的
bool insert(const pair<k, v>& kv)
{
if (_root == nullptr)
{
_root = new node(kv);
_root->_col = black;
return true;
}
node* parent = nullptr;
node* cur = _root;
while (cur)
{
parent = cur;
if (cur->_kv.first < kv.first)
{
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
cur = cur->_left;
}
else
{
return false;
}
}
// 新增节点给红色
cur = new node(kv);
cur->_col = red;
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
// 检测新节点插入后,红黑树的性质是否造到破坏
return true;
}
🧩检测红黑树是否造到破坏
(如果遭到破坏则对当前红黑树进行变色,旋转处理)
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
🌈情况一
cur为红,p为红,g为黑,u存在且为红
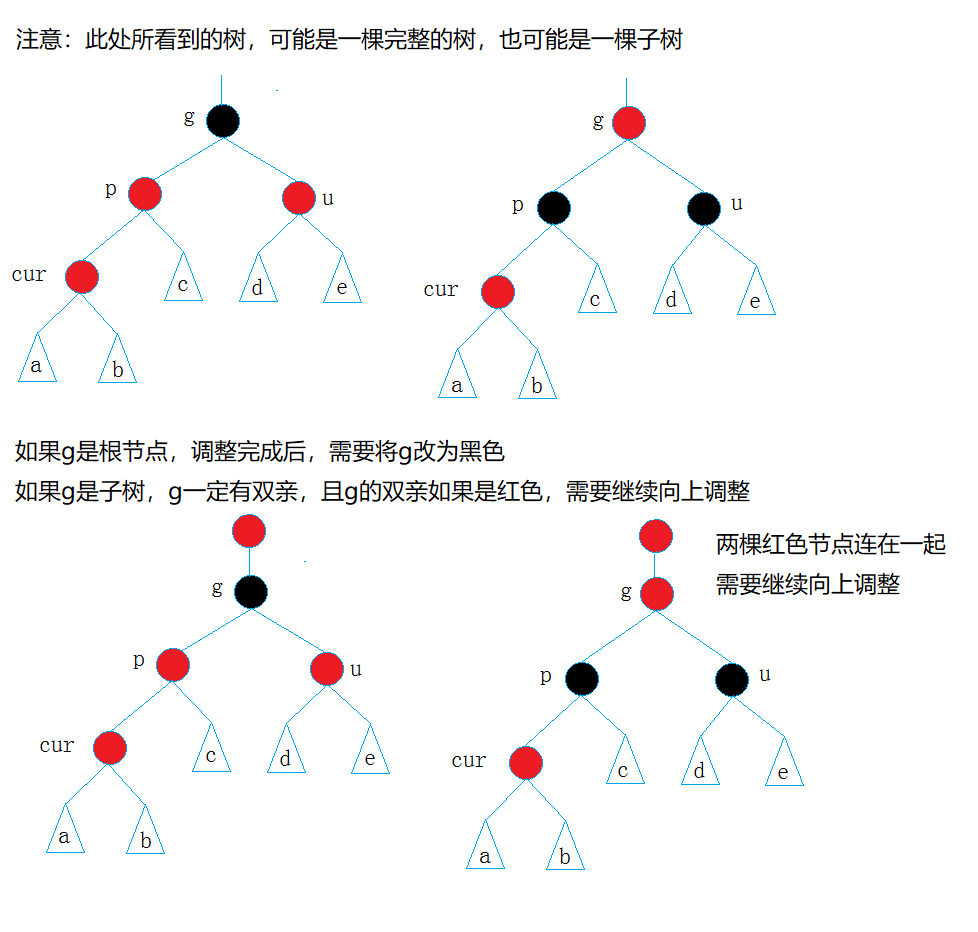
解决方式:将parent,uncle改为黑,g改为红,然后把g当成cur,继续向上调整。
🌈情况二
cur为红,p为红,g为黑,u不存在/u存在且为黑

🌈情况三
cur为红,p为红,g为黑,u不存在/u存在且为黑
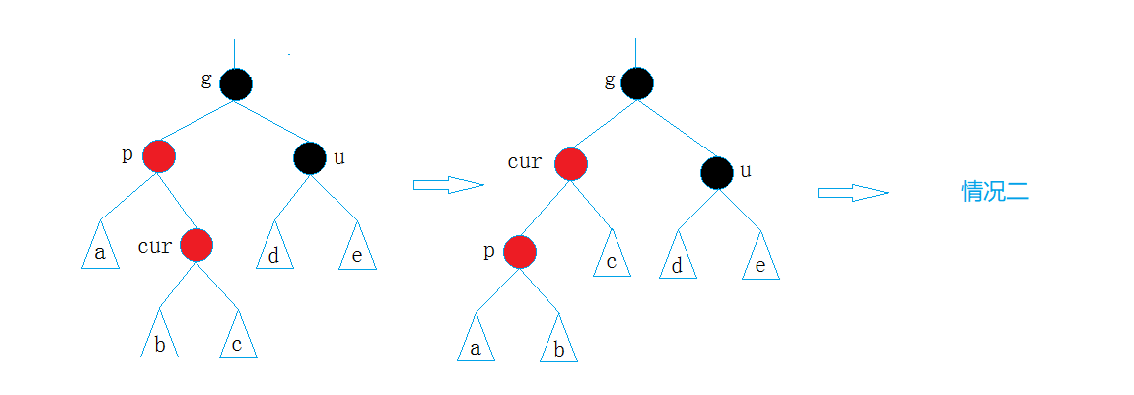
解决方式: p为g的左孩子,cur为p的右孩子,则针对p做左右双旋;p为g的右孩子,cur为p的左孩子,则针对p做右左旋转
检测红黑树是否造到破坏代码演示(c++):
while (parent && parent->_col == red) //当父亲节点为红色,则出现了连续的红色,不符合条件
{
node* grandfather = parent->_parent;
// g
// p u
if (parent == grandfather->_left) {
node* uncle = grandfather->_right;
if (uncle && uncle->_col == red) //叔叔存在并且为红
{
parent->_col = uncle->_col = black;
grandfather->_col = red;
cur = grandfather;
parent = cur->_parent; //往上面走
}
else
{
//u存在且为黑或不存在 ->变色再继续往上处理 + 变色
if (cur == parent->_left) { //cur存在那么cur一定为红色
// g
// p u
//c
//单旋,把p旋转上去,p作为子树根节点,g作为p的右
rotater(grandfather);
parent->_col = black;
grandfather->_col = red;
}
else
{
// g
// p u
// c
//双旋,将cur旋转上去,p作为cur的左,然后再旋转把cur旋转上去,g作为cur右边
rotatel(parent);
rotater(grandfather);
cur->_col = black;
grandfather->_col = red;
}
break;
}
}
else
{
// g
// u p
node* uncle = grandfather->_left;
// 叔叔存在且为红,-》变色即可
if (uncle && uncle->_col == red)
{
parent->_col = uncle->_col = black;
grandfather->_col = red;
// 继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else // 叔叔不存在,或者存在且为黑
{
// 情况二:叔叔不存在或者存在且为黑
// 旋转+变色
// g
// u p
// c
if (cur == parent->_right)
{
rotatel(grandfather);
parent->_col = black;
grandfather->_col = red;
}
else
{
// g
// u p
// c
rotater(parent);
rotatel(grandfather);
cur->_col = black;
grandfather->_col = red;
}
break;
}
}
}
红黑树的旋转和avl树差不多,我们直接上代码回顾以下:
旋转代码示例(c++):
void rotatel(node* parent) // 左旋
{
node* subr = parent->_right;
node* subrl = subr->_left;
parent->_right = subrl;
subr->_left = parent;
node* parentparent = parent->_parent;
parent->_parent = subr;
if (subrl)
subrl->_parent = parent;
// 判断parent是不是根节点
if (_root == parent){
_root = subr;
subr->_parent = nullptr;
}
else{
if (parent == parentparent->_left)
parentparent->_left = subr;
else
parentparent->_right = subr;
subr->_parent = parentparent;
}
}
void rotater(node* parent) // 右旋
{
node* subl = parent->_left;
node* sublr = subl->_right;
parent->_left = sublr;
if (sublr)
sublr->_parent = parent;
node* parentparent = parent->_parent;
subl->_right = parent;
parent->_parent = subl;
if(_root == parent){
_root = subl;
subl->_parent = nullptr;
}
else{
if (parent == parentparent->_left)
parentparent->_left = subl;
else
parentparent->_right = subl;
subl->_parent = parentparent;
}
}
5. 红黑树的验证
📝红黑树的检测分为两步:
中序遍历代码演示(c++):
void inorder()
{
_inorder(_root);
cout << endl;
}
void _inorder(node* root)
{
if (root == nullptr) return;
_inorder(root->_left);
_cout << root->_kv.first << ":" << root->_kv.second << endl;
_inorder(root->_right);
}检测其是否满足红黑树的性质(c++):
bool isbalance()
{
if (_root == nullptr)
return true;
if (_root->_col == red)
{
return false;
}
// 随便找条路径作为参考值
int refnum = 0;
node* cur = _root;
while (cur)
{
if (cur->_col == black)
{
++refnum;
}
cur = cur->_left;
}
return check(_root, 0, refnum);
}
bool check(node* root, int blacknum, const int refnum)
{
if (root == nullptr)
{
//cout << blacknum << endl;
if (refnum != blacknum)
{
cout << "存在黑色节点的数量不相等的路径" << endl;
return false;
}
return true;
}
if (root->_col == red && root->_parent->_col == red)
{
cout << root->_kv.first << "存在连续的红色节点" << endl;
return false;
}
if (root->_col == black)
{
blacknum++;
}
return check(root->_left, blacknum, refnum)
&& check(root->_right, blacknum, refnum);
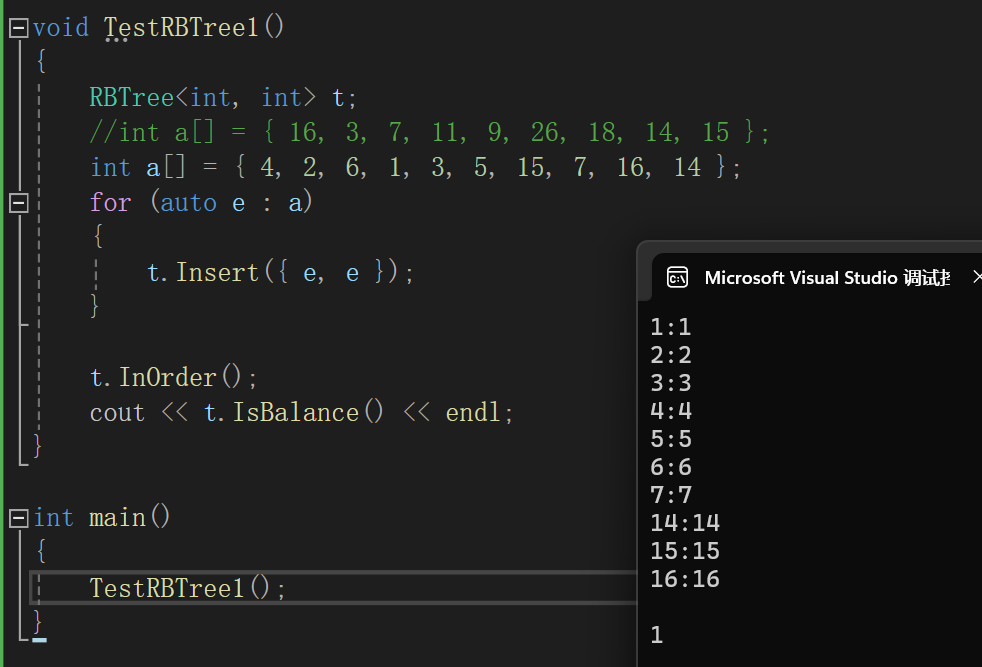
}测试代码用例及结果:
6. 红黑树的完整代码及总结
#include<iostream>
#include<vector>
#include<assert.h>
using namespace std;
enum colour
{
red,
black
};
template<class k, class v>
struct rbtreenode
{
pair<k, v> _kv;
rbtreenode<k, v>* _left;
rbtreenode<k, v>* _right;
rbtreenode<k, v>* _parent;
colour _col;
rbtreenode(const pair<k, v>& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
{}
};
template<class k, class v>
class rbtree
{
typedef rbtreenode<k, v> node;
public:
rbtree() = default;
rbtree(const rbtree<k, v>& t)
{
_root = copy(t._root);
}
rbtree<k, v>& operator=(rbtree<k, v> t)
{
swap(_root, t._root);
return *this;
}
~rbtree()
{
destroy(_root);
_root = nullptr;
}
bool insert(const pair<k, v>& kv)
{
if (_root == nullptr)
{
_root = new node(kv);
_root->_col = black; //根节点默认为黑色
return true;
}
node* parent = nullptr;
node* cur = _root;
while (cur)
{
parent = cur;
if (cur->_kv.first < kv.first) cur = cur->_right;
else if (cur->_kv.first > kv.first) cur = cur->_left;
else return false;
}
cur = new node(kv);
// 新增节点。颜色红色给红色
cur->_col = red;
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
while (parent && parent->_col == red) //当父亲节点为红色,则出现了连续的红色,不符合条件
{
node* grandfather = parent->_parent;
// g
// p u
if (parent == grandfather->_left) {
node* uncle = grandfather->_right;
if (uncle && uncle->_col == red) //叔叔存在并且为红
{
parent->_col = uncle->_col = black;
grandfather->_col = red;
cur = grandfather;
parent = cur->_parent; //往上面走
}
else
{
//u存在且为黑或不存在 ->变色再继续往上处理 + 变色
if (cur == parent->_left) { //cur存在那么cur一定为红色
// g
// p u
//c
//单旋,把p旋转上去,p作为子树根节点,g作为p的右
rotater(grandfather);
parent->_col = black;
grandfather->_col = red;
}
else
{
// g
// p u
// c
//双旋,将cur旋转上去,p作为cur的左,然后再旋转把cur旋转上去,g作为cur右边
rotatel(parent);
rotater(grandfather);
cur->_col = black;
grandfather->_col = red;
}
break;
}
}
else
{
// g
// u p
node* uncle = grandfather->_left;
// 叔叔存在且为红,-》变色即可
if (uncle && uncle->_col == red)
{
parent->_col = uncle->_col = black;
grandfather->_col = red;
// 继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else // 叔叔不存在,或者存在且为黑
{
// 情况二:叔叔不存在或者存在且为黑
// 旋转+变色
// g
// u p
// c
if (cur == parent->_right)
{
rotatel(grandfather);
parent->_col = black;
grandfather->_col = red;
}
else
{
// g
// u p
// c
rotater(parent);
rotatel(grandfather);
cur->_col = black;
grandfather->_col = red;
}
break;
}
}
}
_root->_col = black; //无论什么情况根节点都为黑
return true;
}
void inorder()
{
_inorder(_root);
cout << endl;
}
int height()
{
return _height(_root);
}
int size()
{
return _size(_root);
}
node* find(const k& key)
{
node* cur = _root;
while (cur)
{
if (cur->_kv.first < key)
{
cur = cur->_right;
}
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool isbalance()
{
if (_root == nullptr)
return true;
if (_root->_col == red)
{
return false;
}
// 随便找条路径作为参考值
int refnum = 0;
node* cur = _root;
while (cur)
{
if (cur->_col == black)
{
++refnum;
}
cur = cur->_left;
}
return check(_root, 0, refnum);
}
private:
bool check(node* root, int blacknum, const int refnum)
{
if (root == nullptr)
{
//cout << blacknum << endl;
if (refnum != blacknum)
{
cout << "存在黑色节点的数量不相等的路径" << endl;
return false;
}
return true;
}
if (root->_col == red && root->_parent->_col == red)
{
cout << root->_kv.first << "存在连续的红色节点" << endl;
return false;
}
if (root->_col == black)
{
blacknum++;
}
return check(root->_left, blacknum, refnum)
&& check(root->_right, blacknum, refnum);
}
int _size(node* root)
{
return root == nullptr ? 0 : _size(root->_left) + _size(root->_right) + 1;
}
int _height(node* root)
{
if (root == nullptr)
return 0;
int leftheight = _height(root->_left);
int rightheight = _height(root->_right);
return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}
void _inorder(node* root)
{
if (root == nullptr)
{
return;
}
_inorder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_inorder(root->_right);
}
void rotatel(node* parent)
{
_rotatenum++;
node* subr = parent->_right;
node* subrl = subr->_left;
parent->_right = subrl;
if (subrl)
subrl->_parent = parent;
node* parentparent = parent->_parent;
subr->_left = parent;
parent->_parent = subr;
if (parentparent == nullptr)
{
_root = subr;
subr->_parent = nullptr;
}
else
{
if (parent == parentparent->_left)
{
parentparent->_left = subr;
}
else
{
parentparent->_right = subr;
}
subr->_parent = parentparent;
}
}
void rotater(node* parent)
{
_rotatenum++;
node* subl = parent->_left;
node* sublr = subl->_right;
parent->_left = sublr;
if (sublr)
sublr->_parent = parent;
node* parentparent = parent->_parent;
subl->_right = parent;
parent->_parent = subl;
if (parentparent == nullptr)
{
_root = subl;
subl->_parent = nullptr;
}
else
{
if (parent == parentparent->_left)
{
parentparent->_left = subl;
}
else
{
parentparent->_right = subl;
}
subl->_parent = parentparent;
}
}
void destroy(node* root)
{
if (root == nullptr)
return;
destroy(root->_left);
destroy(root->_right);
delete root;
}
node* copy(node* root)
{
if (root == nullptr) return nullptr;
node* newroot = new node(root->_kv);
newroot->_left = copy(root->_left);
newroot->_right = copy(root->_right);
return newroot;
}
private:
node* _root = nullptr;
public:
int _rotatenum = 0;
};
void testrbtree1()
{
rbtree<int, int> t;
//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
for (auto e : a)
{
t.insert({ e, e });
}
t.inorder();
cout << t.isbalance() << endl;
}


发表评论