


❀哈希
前言:在数字世界的浩瀚宇宙中,哈希算法如同星辰般璀璨,以其独特的方式照亮了数据处理与信息安全的道路。它们不仅是现代计算体系中的基石,更是连接数据安全、高效检索与分布式系统的桥梁。然而,当我们谈论哈希时,往往更多地聚焦于其上层应用与宏观效果,而忽视了支撑这些奇迹的底层机制与实现细节
通过本文的阅读,希望大家不仅能够深入理解哈希算法的底层机制与实现细节,还能够掌握其在实际应用中的关键技术与最佳实践
让我们一起踏上学习的旅程,探索它带来的无尽可能!
📚1. unordered系列关联式容器
🧩unordered_map
🌸接口说明
unordered_map的构造
| 函数声明 | 功能介绍 |
|---|---|
| unordered_map | 构造不同格式的unordered_map对象 |
unordered_map的容量
| 函数声明 | 功能介绍 |
|---|---|
| bool empty() const | 检测unordered_map是否为空 |
| size_t size() const | 获取unordered_map的有效元素个数 |
unordered_map的迭代器
| 函数声明 | 功能介绍 |
|---|---|
| begin | 返回unordered_map第一个元素的迭代器 |
| end | 返回unordered_map最后一个元素下一个位置的迭代器 |
| cbegin | 返回unordered_map第一个元素的const迭代器 |
| cend | 返回unordered_map最后一个元素下一个位置的const迭代器 |
unordered_map的元素访问
| 函数声明 | 功能介绍 |
|---|---|
| operator[ ] | 返回与key对应的value,没有一个默认值 |
unordered_map的查询
| 函数声明 | 功能介绍 |
|---|---|
| iterator find(const k& key) | 返回key在哈希桶中的位置 |
| size_t count(const k& key) | 返回哈希桶中关键码为key的键值对的个数 |
unordered_map的修改操作
| 函数声明 | 功能介绍 |
|---|---|
| insert | 向容器中插入键值对 |
| erase | 删除容器中的键值对 |
| void clear() | 清空容器中有效元素个数 |
| void swap(unordered_map&) | 交换两个容器中的元素 |
🧩unordered_set
🌺接口说明
unordered_set的构造
| 函数声明 | 功能介绍 |
|---|---|
| unordered_set | 构造不同格式的unordered_set对象 |
unordered_set的容量
| 函数声明 | 功能介绍 |
|---|---|
| bool empty() const | 检测unordered_set是否为空 |
| size_t size() const | 获取unordered_set的有效元素个数 |
unordered_set的迭代器
| 函数声明 | 功能介绍 |
|---|---|
| begin | 返回unordered_set第一个元素的迭代器 |
| end | 返回unordered_set最后一个元素下一个位置的迭代器 |
| cbegin | 返回unordered_set第一个元素的const迭代器 |
| cend | 返回unordered_set最后一个元素下一个位置的const迭代器 |
unordered_set的查询
| 函数声明 | 功能介绍 |
|---|---|
| iterator find(const k& key) | 返回key在哈希桶中的位置 |
| size_t count(const k& key) | 使用特定键对元素进行计数 |
unordered_set的修改操作
| 函数声明 | 功能介绍 |
|---|---|
| insert | 向容器中插入键值对 |
| erase | 删除容器中的键值对 |
| void clear() | 清空容器中有效元素个数 |
| void swap(unordered_set&) | 交换两个容器中的元素 |
这里介绍的两个unordered系列的关联式容器和map和set还是有点相似的,我们再来几道题目来熟练掌握它们的使用
重复n次的元素
两个数组的交集
📜2. 底层结构
🌈哈希概念
可以不经过任何比较,一次直接从表中得到要搜索的元素。如果构造一种存储结构,通过某种函数(hashfunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素,这就是最理想的搜索方法
注意:哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称为哈希表(hash table)(或者称散列表)
示例:数据集合{1,7,6,4,5,9};
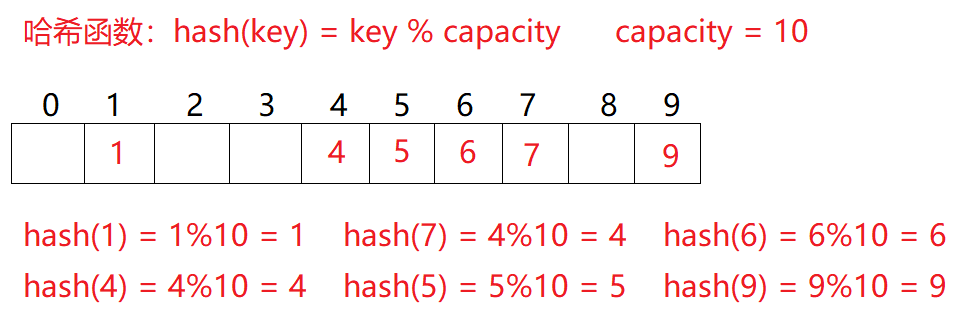
用该方法进行搜索不必进行多次关键码的比较,因此搜索的速度比较快,但是有成千上万的数,总会有几个数,取余后相等,那我们该怎么存放值呢?
hash(5) = 5 % 10 = 5;
hash(55) = 55 % 10 = 5;
这时就要引入一个新的概念 -> 哈希冲突
🌞哈希冲突
我们把把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”
🌙哈希函数
哈希函数设计原则
常见哈希函数
直接定址法–(常用)
除留余数法–(常用)
注意:哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突
⭐哈希冲突解决
🌄闭散列
线性探测
如果和上面讲的一样,现在需要插入元素55,先通过哈希函数计算哈希地址,hashaddr为5,
因此55理论上应该插在该位置,但是该位置已经放了值为5的元素,即发生哈希冲突
- 插入
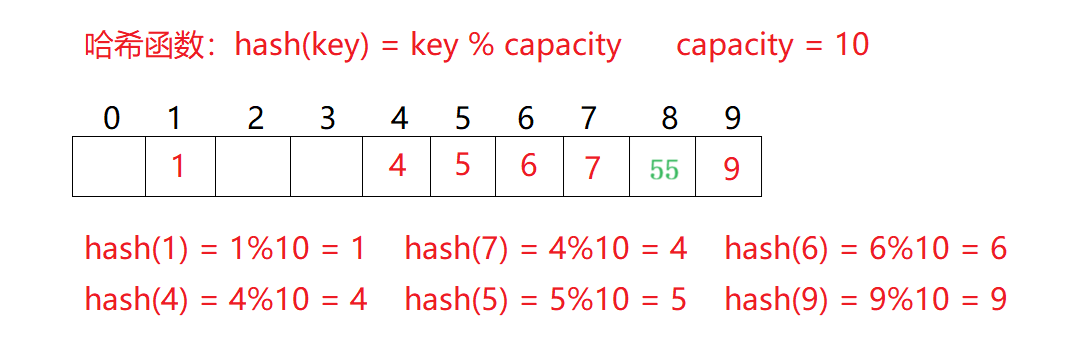
- 删除
// 哈希表每个空间三种状态
// empty此位置空, exist此位置已经有元素, delete元素已经删除
enum state
{
empty,
exist,
delete
};
线性探测的实现
template<class k, class v>
struct hashdata
{
pair<k, v> _kv;
status _s;
};
template<class k, class v, class hash = hashfunc<k>>
class hashtable
{
public:
hashtable()
{
_tables.resize(10);
}
bool insert(const pair<k, v>& kv)
{
if (find(kv.first))
{
return false;
}
// 负载因子 -> 哈希表扩容
if (_n * 10 / _tables.size() == 7)
{
size_t newsize = _tables.size() * 2;
hashtable<k, v, hash> newht;
newht._tables.resize(newsize);
// 遍历旧表
for (size_t i = 0; i < _tables.size(); i++)
{
if(_tables[i]._s == exist)
{
// 复用insert
newht.insert(_tables[i]._kv);
}
}
// 交换两个表的数据
_tables.swap(newht._tables);
}
hash hf;
// 线性探测
size_t hashi = hf(kv.first) % _tables.size();
while (_tables[hashi]._s == exist)
{
hashi++;
hashi %= _tables.size();
}
_tables[hashi]._kv = kv;
_tables[hashi]._s = exist;
++_n;
return true;
}
hashdata<k, v>* find(const k& key)
{
hash hf;
size_t hashi = hf(key) % _tables.size();
while (_tables[hashi]._s != empty)
{
if (_tables[hashi]._kv.first == key)
{
return &_tables[hashi];
}
hashi++;
hashi %= _tables.size();
}
return null;
}
// 伪删除法
bool erase(const k& key)
{
hashdata<k, v>* ret = find(key);
if (ret)
{
ret->_s = delete;
--_n;
return true;
}
else
{
return false;
}
}
private:
vector < hashdata<k, v>> _tables;
size_t _n = 0; // 储存的关键字数据的个数
};
关于哈希表的取余
当我们的key不是整形的时候(常见的是string),我们该怎么计算它的hashi? 这里又得依靠我们的仿函数hashfunc,又因为我们string也是很常见的,我们将模板特化一下
template<class k>
struct hashfunc
{
size_t operator()(const k& key)
{
return (size_t)key;
}
};
template<>
struct hashfunc<string>
{
size_t operator()(const string& key)
{
size_t hash = 0;
for (auto e : key)
{
// 避免因为顺序不一样而产生一样的值 bkdr
// 避免 abc,acb同值不同意
e *= 31;
hash += e;
}
return hash;
}
};
关于哈希表的扩容

- 线性探测优点:实现非常简单
- 线性探测缺点:一旦发生哈希冲突,所有的冲突连在一起,容易产生数据“堆积”,即:不同关键码占据了可利用的空位置,使得寻找某关键码的位置需要许多次比较,导致搜索效率降低
🏞️开散列
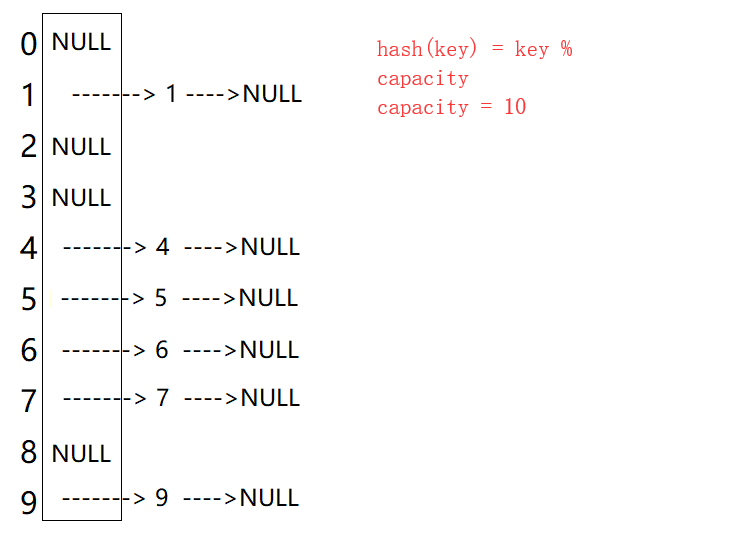
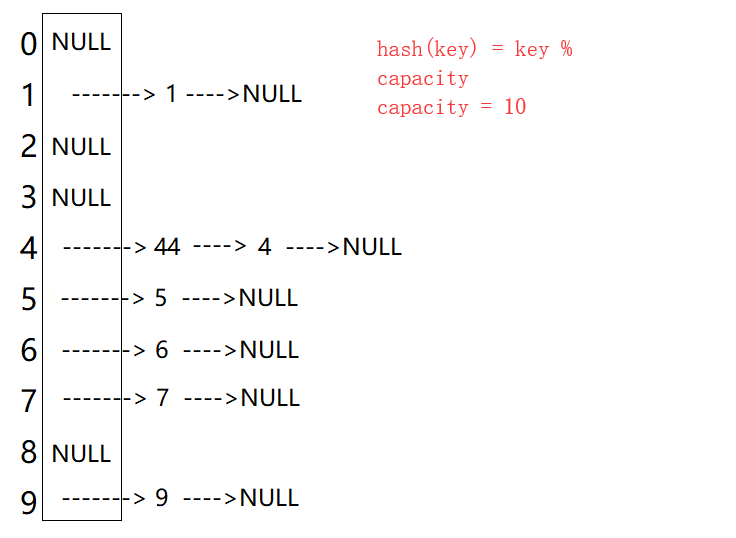
注意:开散列中每个桶中放的都是发生哈希冲突的元素
开散列实现
template<class k, class v>
struct hashnode
{
hashnode* _next;
pair<k, v> _kv;
hashnode(const pair<k, v>& kv)
:_kv(kv)
,_next(nullptr)
{}
};
template<class k, class v, class hash = hashfunc<k>>
class hashtable
{
typedef hashnode<k, v> node;
public:
hashtable()
{
_tables.resize(10);
}
~hashtable()
{
for (size_t i = 0; i < _tables.size(); i++)
{
node* cur = _tables[i];
while (cur)
{
node* _next = cur->_next;
delete cur;
cur = _next;
}
_tables[i] = nullptr;
}
}
bool insert(const pair<k, v>& kv)
{
hash hf;
if (find(kv.first))
{
return false;
}
// 负载因子
if (_n == _tables.size())
{
vector<node*> newtables;
newtables.resize(_tables.size() * 2);
// 遍历旧表
for (size_t i = 0; i < _tables.size(); i++)
{
node* cur = _tables[i];
while (cur)
{
node* next = cur->_next;
// 挪动到新表
size_t hashi = hf(cur->_data) % newtables.size();
cur->_next = newtables[hashi];
newtables[hashi] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newtables);
}
size_t hashi = hf(kv.first) % _tables.size();
node* newnode = new node(kv);
// 头插
newnode->_next = _tables[hashi];
_tables[hashi] = newnode;
++_n;
return true;
}
node* find(const k& key)
{
hash hf;
size_t hashi = hf(key) % _tables.size();
node* cur = _tables[hashi];
while (cur)
{
if (cur->_kv.first) == key)
{
return cur;
}
cur = cur->_next;
}
return nullptr;
}
bool erase(const k& key)
{
hash hf;
size_t hashi = hf(key) % _tables.size();
node* cur = _tables[hashi];
node* prev = nullptr; // 记录上一个节点
while (cur)
{
if (cur->_kv.first == key)
{
if (prev == nullptr)
{
_tables[hashi] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}
private:
vector<node*> _tables;
size_t _n = 0;
};
开散列增容
代码示例:
if (_n == _tables.size())
{
vector<node*> newtables;
newtables.resize(_tables.size() * 2);
// 遍历旧表
for (size_t i = 0; i < _tables.size(); i++)
{
node* cur = _tables[i];
while (cur)
{
node* next = cur->_next;
// 挪动到新表
size_t hashi = hf(cur->_data) % newtables.size();
cur->_next = newtables[hashi];
newtables[hashi] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newtables);
}
⛰️开散列与闭散列比较
📖3. 总结
随着技术的不断进步,哈希表作为数据处理领域的基石,其重要性日益凸显。通过本文的探讨,我们深入剖析了哈希表的底层实现原理,从哈希函数的选择、冲突解决策略到动态扩容机制,每一个细节都展现了人类智慧在数据处理领域的卓越成就
希望各位在未来的学习与工作中,保持对知识的渴望与追求,勇于挑战自我,不断探索未知领域。相信在不久的将来,你们定能在数据处理的广阔舞台上大放异彩!

希望本文能够为你提供有益的参考和启示,让我们一起在编程的道路上不断前行!
谢谢大家支持本篇到这里就结束了,祝大家天天开心!


发表评论