
1. 前言
相信大家之前或多或少都听说过b树或b+树,奔跑文章将从认识b树到手撕b树(注意不是b减树,是b树),一步一步带你吃透它!
本章重点:
b树学习难度较大, 请大家耐心学习
2. 初识b树
首先要明确一点, b树是一个搜索结构.那么它和传统的搜索结构,比如红黑树, 哈希等有什么区别呢?先请看下图:
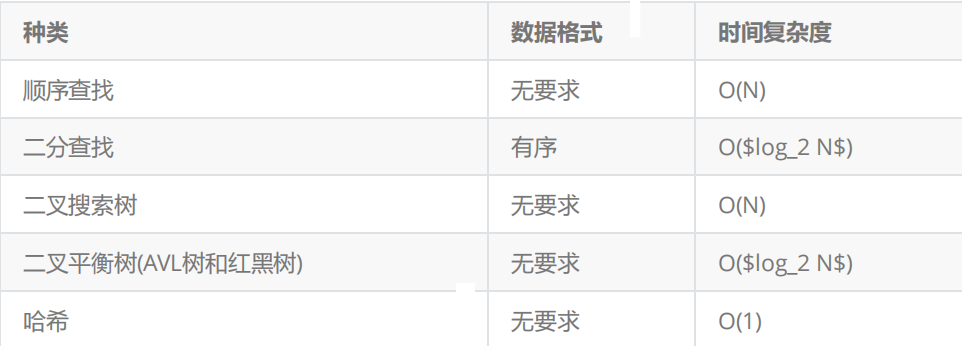
一棵m阶(m>2)的b树,是一棵平衡的m路平衡搜索树,可以是空树或者满足一下性质:
- 根节点至少有两个孩子
- 每个分支节点都包含k-1个关键字和k个孩子,其中 ceil(m/2) ≤ k ≤ m ceil是向上取整函数
- 每个叶子节点都包含k-1个关键字,其中 ceil(m/2) ≤ k ≤ m
- 所有的叶子节点都在同一层
- 每个节点中的关键字从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域划分
- 每个结点的结构为:(n,a0,k1,a1,k2,a2,… ,kn,an)其中,ki(1≤i≤n)为关键字,且ki<ki+1(1≤i≤n-1)。ai(0≤i≤n)为指向子树根结点的指针。且ai所指子树所有结点中的关键字均小于ki+1。n为结点中关键字的个数,满足ceil(m/2)-1≤n≤m-1。
3. b树的插入分析
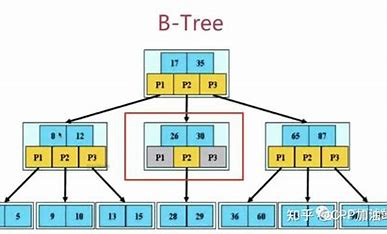
现在我们使用一个b树做插入的案例,来解释b树的这些性质. 设m=3,即三叉树,每个节点存两个数据,和三个孩子区域的划分
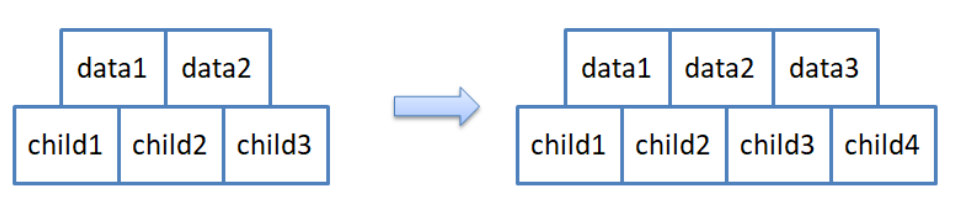
注意:孩子永远比数据多一个。
用后面的图可以更好的演示b树的分裂
用序列{53, 139, 75, 49, 145, 36, 101}构建b树的过程如下:
第一步:
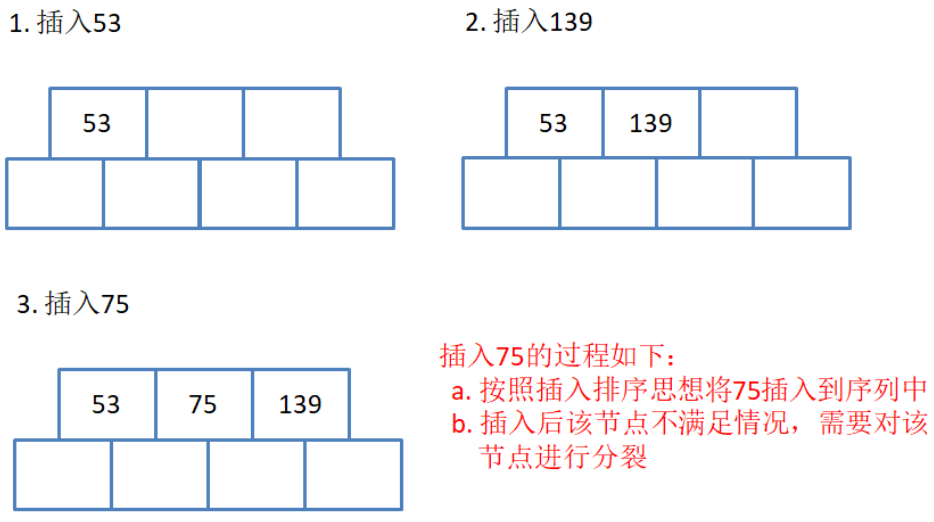
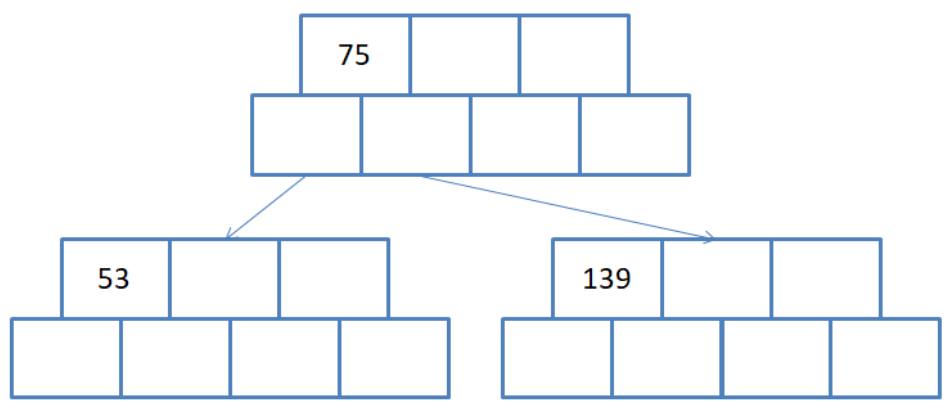
这样做恰好满足了b树的一个性质: a1,k1,a2,k2数组中, a1,这里代表75的左孩子,是小于k1的,k1也就是75. 而a2,对应是139所在的节点, 是大于k1的.
第二步:
注意: b树的插入都是在叶子节点进行的,当叶子节点不符合b树规则时才会向上形成新的节点,也就是所谓的分裂操作
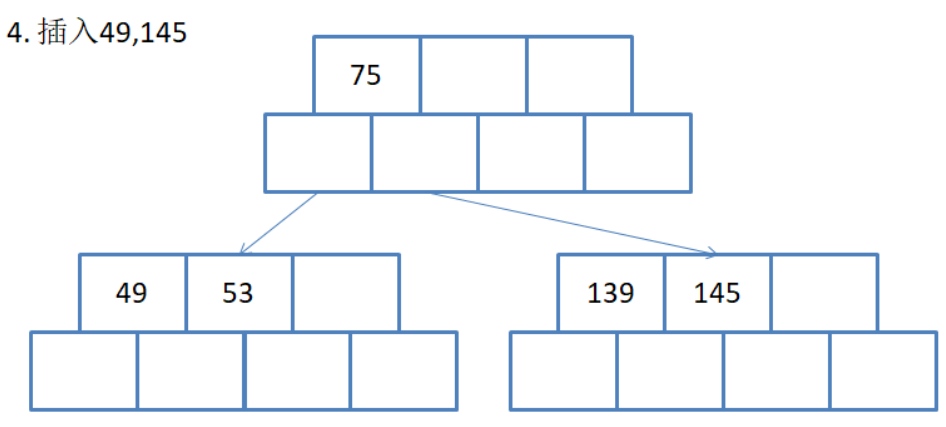
这两次插入都没违反规则
第三步:
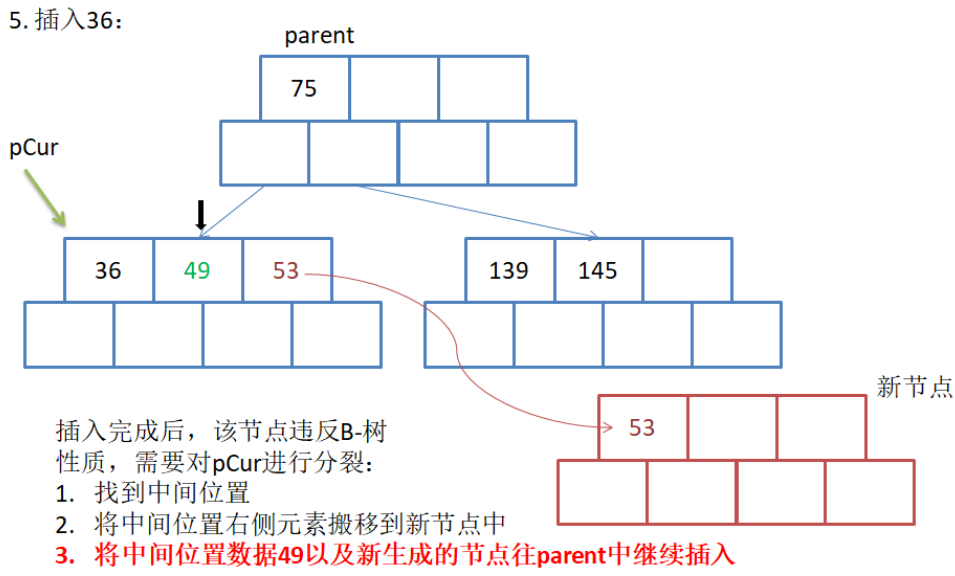
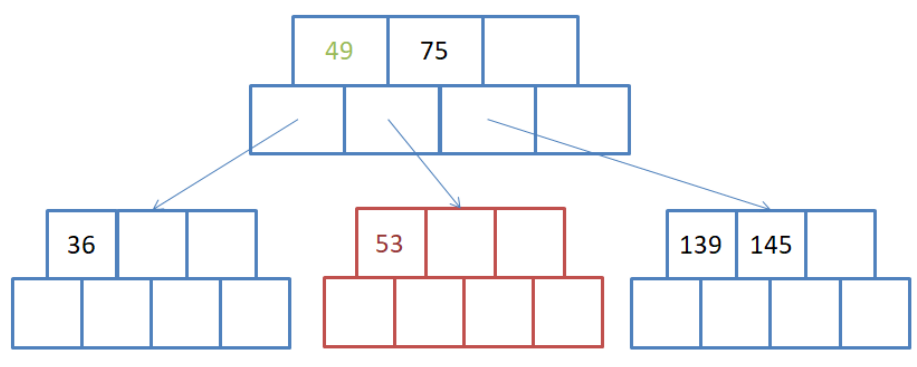
并且也要满足上面所说的a1<k1<a2<k2<a3
注意, 节点中只存了两个数据, 数据下面的数据存储的是孩子节点的地址
第四步:
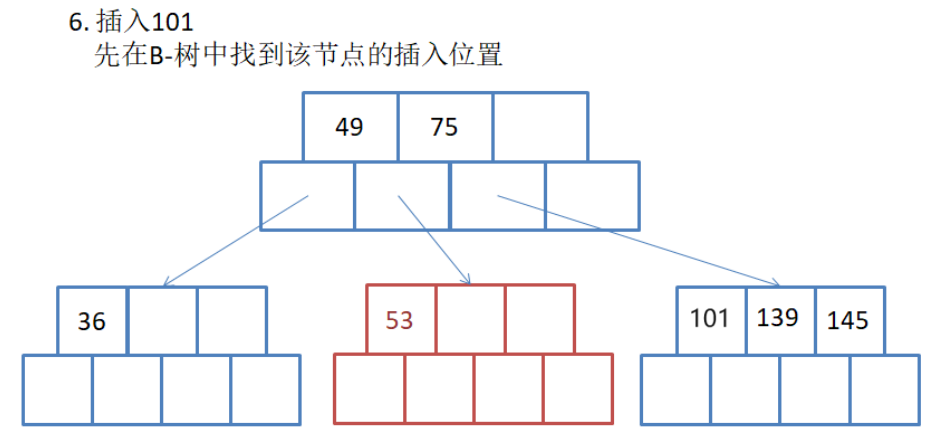
4. b树的规则再分析
了解了b树是如何分裂了之后,我们在倒过来看看b树的规则,就好理解多了:
- 根节点至少有两个孩子: 为什么呢?因为b树进行一次分裂之后, 至少会分裂出两个孩子.
- 第二点解释: 孩子的数量永远比数据多一个,k一般就取值为m
剩下的我相信大家都能理解了
5. b树模拟实现
首先是基本的b树节点的结构:
template<class k, size_t m>
struct btreenode
{
k _keys[m];//m个孩子,m-1个关键字.但为了方便插入再分裂,定义为m个关键字,m+1个child
btreenode<k, m>* _childs[m + 1];
btreenode<k, m>* _parent; //存父亲节点,分裂时需要用
size_t _num;//记录实际存储了多少个key(记录key或child都行)
btreenode() {
for (int i = 0; i < m; i++) {
_keys[i] = k();
_childs[i] = nullptr;
}
_num = 0;
_childs[m] = nullptr;
_parent = nullptr;
}
};
//数据是存在磁盘, k就是磁盘地址
template<class k,size_t m>
class btree
{
typedef btreenode<k, m> node;
private:
node* _root = nullptr;
};
pair<node*, int> find(const k& key)//返回这个值以及它的下标
{
node* cur = _root;
//记录路径,最后会获得叶子节点
node* prev = nullptr;
while (cur)
{
size_t i = 0;
//下面的逻辑表示在一个节点中查找
while (cur && i < cur->_num)
{
//在左孩子中去找,左孩子的数组的下标等于当前下标
if (key < cur->_keys[i])
break;
//比当前值大就往后++,直到值比key大
else if (key > cur->_keys[i])
i++;
else return make_pair(cur, i);
}
//往孩子去跳
prev = cur;
cur = cur->_childs[i];
}
return make_pair(prev, -1);
}
//给一个节点的指针,插入key和children
void insertkey(node* node, const k& key, node* children)
{
int end = node->_num - 1;
//插入排序,若插入的数据较小,原先的数据会往后移动
while (end >= 0)
{
if (node->_keys[end] > key)
{
//不仅要挪动key,还要挪动它的右孩子
node->_keys[end + 1] = node->_keys[end];
node->_childs[end + 2] = node->_childs[end + 1];
end--;
}
else break;
}
//插入在end位置的后面,可能比所有值都小,end+1=0
node->_keys[end + 1] = key;
node->_childs[end + 2] = children;
if (children)
children->_parent = node;
node->_num++;
}
bool insert(const k& key) {
//第一次插入的逻辑
if (_root == nullptr) {
_root = new node;
_root->_keys[0] = key;
_root->_num++;
return true;
}
pair<node*, int> ret = find(key);
//key已经存在,插入失败
if (ret.second >= 0)
return false;
//若key不存在,find顺便带回来了要插入的叶子节点
node* cur = ret.first;
k newkey = key;
node* children = nullptr;
//循环每次往cur插入newkey和child
while (1) {
insertkey(cur, newkey,children);
//判断此节点满没有
if (cur->_num < m)
return true;
//需要分裂,创建一个兄弟节点
else {
size_t mid = m / 2;
//[mid+1,m-1]给兄弟
node* brother = new node;
int j = 0;
for (int i = mid + 1; i <= m - 1; i++)
{
brother->_keys[j] = cur->_keys[i];
//不仅仅要拷贝走一半的数据,并且还需要将这一半数据的孩子一起拷贝给brother
//拷走一个key就要拷走这个key的左孩子.孩子的父亲变了,需要修改
brother->_childs[j] = cur->_childs[i];
if (cur->_childs[i])
cur->_childs[i]->_parent = brother;
//将拷贝走的数据重置
cur->_keys[i] = k();
cur->_childs[i] = nullptr;
j++;
}
//拷贝完后还有最后一个右孩子,最右的孩子需要拷贝走
brother->_childs[j] = cur->_childs[m];
if (cur->_childs[m])
cur->_childs[m]->_parent = brother;
cur->_childs[m] = nullptr;
brother->_num = j;
cur->_num -= (j + 1);//拷走了j个,mid也被提取了
//分裂后转换成往cur->parent插入mid和brother
k midkey = cur->_keys[mid];
//cur等于空证明分裂的是根节点
cur->_keys[mid] = k();
if (cur->_parent == nullptr)
{
_root = new node;
_root->_keys[0] = midkey;
_root->_childs[0] = cur;
_root->_childs[1] = brother;
_root->_num = 1;
cur->_parent = _root;
brother->_parent = _root;
break;
}
else {
newkey = midkey;
//中位数给父亲了,也重置一下
children = brother;
cur = cur->_parent;
}
}
}
return true;
}
6. 总结以及拓展
b树模块的重点是它的分裂逻辑和使用场景, 并且b树在实际生产中运行并不多, 因为有更好的数据结构: b+树或是b*树来代替它. 但是学习后两者的前提是需要你知晓b树的性质, 所以学习不是一蹴而就的,是需要持之以恒的





发表评论