NumPy 数组花式索引(Fancy Indexing)的实现_Python

前面的博客分享了我对于numpy数组索引的学习心得——如何使用简单索引（例如 arr[0]）、切片（例如 arr[:5]）和布尔掩码（例如 arr[arr > 0]）来访问和修改数组的部分内容。
这里，我们将介绍另一种数组索引方式，称为花式或矢量化索引，其中我们用索引数组代替单个标量。
这种方式可以让我们非常快速地访问和修改数组中复杂子集的值。

探索花式索引

花式索引在概念上很简单：它指的是通过传递一个索引数组来一次性访问多个数组元素。
以下面的数组为例：

import numpy as np
rng = np.random.default_rng(seed=1024)

x = rng.integers(100, size=10)
print(x)

[55 32 87 25  8 37 74 88 38 62]

假设我们想要访问三个不同的元素。我们可以这样做：

[x[3], x[9], x[8]]

[np.int64(25), np.int64(62), np.int64(38)]

另外，我们也可以传递一个索引列表或数组来获得相同的结果：

ind = [3, 9, 8]
x[ind]

array([25, 62, 38])

当使用索引数组时，结果的形状反映的是索引数组的形状，而不是被索引数组的形状：

ind = np.array([[3, 7],
                [4, 5]])
x[ind]

array([[25, 88],
       [ 8, 37]])

花式索引同样适用于多维数组。请看下面的数组：

x = np.arange(30).reshape((5, 6))
x

array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17],
       [18, 19, 20, 21, 22, 23],
       [24, 25, 26, 27, 28, 29]])

像标准索引一样，第一个索引表示行，第二个索引表示列：

row = np.array([0, 1, 2])
col = np.array([2, 1, 3])
x[row, col]

array([ 2,  7, 15])

注意，结果中的第一个值是 x[0, 2]，第二个是 x[1, 1]，第三个是 x[2, 3]。
在花式索引中，索引的配对遵循了数组的广播机制中提到的所有广播规则。
因此，例如，如果我们在索引中结合使用列向量和行向量，就会得到一个二维的结果：

x[row[:, np.newaxis], col]

array([[ 2,  1,  3],
       [ 8,  7,  9],
       [14, 13, 15]])

这里，每个行索引值都会与每个列向量进行匹配，这与我们在算术运算广播中看到的方式完全一致。
例如：

row[:, np.newaxis] * col

array([[0, 0, 0],
       [2, 1, 3],
       [4, 2, 6]])

在使用花式索引时，务必要记住：返回值的形状反映的是索引的广播后形状，而不是被索引数组的形状。

组合索引

为了实现更强大的操作，花式索引可以与我们之前见过的其他索引方式结合使用。例如，给定数组 x：

print(x)

[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]
 [12 13 14 15 16 17]
 [18 19 20 21 22 23]
 [24 25 26 27 28 29]]

我们可以将花式索引与简单索引结合使用：

x[2, [2, 0, 1]]

array([14, 12, 13])

我们还可以将花式索引与切片结合使用：

x[1:, [2, 0, 1]]

array([[ 8,  6,  7],
       [14, 12, 13],
       [20, 18, 19],
       [26, 24, 25]])

我们还可以将花式索引与掩码（布尔索引）结合使用：

mask = np.array([true, false, true, false, false, false])
x[row[:, np.newaxis], mask]

array([[ 0,  2],
       [ 6,  8],
       [12, 14]])

所有这些索引方式的组合，使我们能够非常灵活、高效地访问和修改数组的值。

示例：选择随机点

花式索引的一个常见用途是从矩阵中选择部分行的子集。
例如，我们可能有一个 n × d n \times d n×d 的矩阵，表示 n n n 个 d d d 维空间中的点，比如下面这些从二维正态分布中抽取的点：

mean = [0, 0]
cov = [[1, 2],
       [2, 5]]
x = rng.multivariate_normal(mean, cov, 100)
x.shape

(100, 2)

使用matplotlib，我们可以将这些点可视化为散点图（见下图）：

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-v0_8-whitegrid')

plt.scatter(x[:, 0], x[:, 1]);

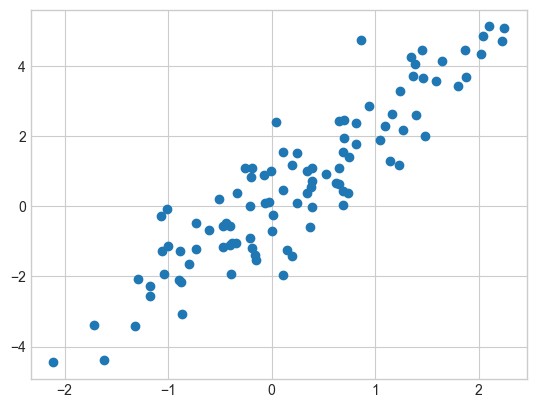
让我们用花式索引选择 20 个随机点。我们将首先随机选择 20 个不重复的索引，然后用这些索引来选取原数组中的一部分：

indices = np.random.choice(x.shape[0], 20, replace=false)
indices

array([87, 77, 55, 54, 34, 76, 30, 12, 61, 90, 29, 94,  8, 91, 81, 97, 74,
        5, 99, 20], dtype=int32)

selection = x[indices]  # 使用花式索引选择点
selection.shape

(20, 2)

现在，为了查看哪些点被选中了，我们将在被选中的点的位置上叠加大圆圈（见下图）：

plt.scatter(x[:, 0], x[:, 1], alpha=0.3)
plt.scatter(selection[:, 0], selection[:, 1],
            facecolor='none', edgecolor='black', s=200);

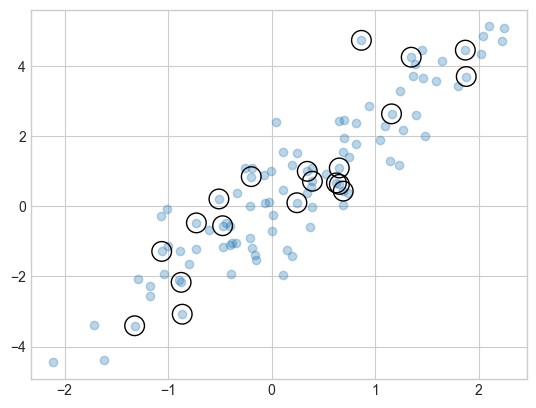
这种策略常用于快速划分数据集，例如在统计模型验证（如超参数与模型验证）中进行训练/测试集分割，以及在采样方法中用于解答统计问题。

用花式索引修改值

正如花式索引可以用来访问数组的部分内容，它也可以用来修改数组的部分内容。
例如，假设我们有一个索引数组，并希望将数组中对应的元素设置为某个值：

x = np.arange(10)
i = np.array([2, 1, 8, 4])
x[i] = 99
print(x)

[ 0 99 99  3 99  5  6  7 99  9]

我们可以对其使用任何赋值类型的运算符。例如：

x[i] -= 10
print(x)

[ 0 89 89  3 89  5  6  7 89  9]

请注意，对于这些操作，如果索引中有重复项，可能会导致一些意想不到的结果。请看下面的例子：

x = np.zeros(10)
x[[0, 0]] = [4, 6]
print(x)

[6. 0. 0. 0. 0. 0. 0. 0. 0. 0.]

4 到哪去了？这个操作首先执行 x[0] = 4，然后执行 x[0] = 6。
结果当然是 x[0] 的值为 6。

这很合理，但请考虑下面这个操作：

i = [2, 3, 3, 4, 4, 4]
x[i] += 1
x

array([6., 0., 1., 1., 1., 0., 0., 0., 0., 0.])

你可能会期望 x[3] 的值为 2，x[4] 的值为 3，因为每个索引重复的次数就是它们应该增加的次数。为什么实际不是这样呢？
从概念上讲，这是因为 x[i] += 1 实际上等价于 x[i] = x[i] + 1。x[i] + 1 会先被整体计算出来，然后再把结果赋值回 x 的这些索引位置。
这样一来，实际上是赋值操作被多次执行，而不是累加操作被多次执行，这就导致了看起来不太直观的结果。

那么如果你想要每个索引都累加多次该怎么办？这时可以使用 ufunc 的 at 方法，如下所示：

x = np.zeros(10)
np.add.at(x, i, 1)
print(x)

[0. 0. 1. 2. 3. 0. 0. 0. 0. 0.]

at 方法会在指定的索引（这里是 i）处对给定的操作符（这里是 1）进行原地应用。
另一个在原理上类似的方法是 ufunc 的 reduceat 方法，你可以在 numpy 官方文档中了解更多信息。

示例：数据分箱（binning data）

你可以利用这些思想高效地对数据进行自定义分箱计算。
例如，假设我们有 100 个数值，并希望快速判断它们分别落在一组分箱（bins）中的哪个区间。
我们可以像下面这样用 ufunc.at 来实现：

rng = np.random.default_rng(seed=1024)
x = rng.normal(size=100)

# 手工计算直方图
bins = np.linspace(-5, 5, 20)
counts = np.zeros_like(bins)

# 为每个 x 找到合适的分箱
i = np.searchsorted(bins, x)

# 将这些索引对应的分箱加一
np.add.at(counts, i, 1)

现在，counts 反映了每个分箱中的点的数量——换句话说，就是一个直方图（见下图）：

# 绘制直方图
plt.plot(bins, counts, drawstyle='steps');

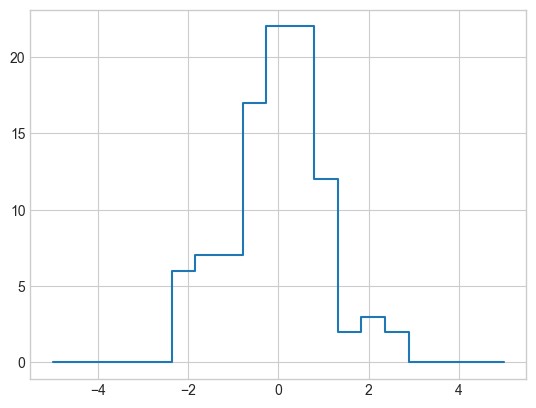
当然，如果每次想要绘制直方图都要手动实现上述步骤会很不方便。
这也是为什么 matplotlib 提供了 plt.hist 例程，它可以用一行代码完成相同的操作：

plt.hist(x, bins, histtype='step');

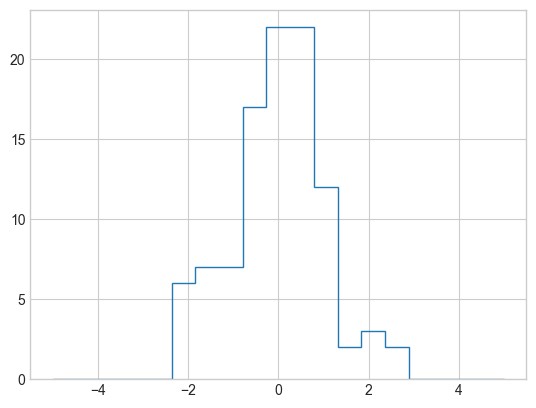
这个函数会生成一个与刚才几乎相同的图像。
在计算分箱时，matplotlib 实际上调用了 np.histogram 函数，其实现方式与我们手动实现的非常类似。我们可以在这里对比两者：

print(f"numpy 直方图 ({len(x)} 点):")
%timeit counts, edges = np.histogram(x, bins)

print(f"自定义直方图 ({len(x)} 点):")
%timeit np.add.at(counts, np.searchsorted(bins, x), 1)

numpy 直方图 (100 点):
6.43 μs ± 68.1 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
自定义直方图 (100 点):
5.53 μs ± 86.7 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

我们自己的一行算法居然比 numpy 中的优化算法快！这是怎么回事？如果你深入查看 np.histogram 的源码（在 ipython 中输入 np.histogram?? 即可），你会发现它比我们简单的“查找并计数”要复杂得多；这是因为 numpy 的算法更加灵活，尤其是在数据点数量很大时，专门针对更好的性能进行了设计：

x = rng.normal(size=1000000)
print(f"numpy 直方图 ({len(x)} 点):")
%timeit counts, edges = np.histogram(x, bins)

print(f"自定义直方图 ({len(x)} 点):")
%timeit np.add.at(counts, np.searchsorted(bins, x), 1)

numpy 直方图 (1000000 点):
5.75 ms ± 107 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
自定义直方图 (1000000 点):
48.7 ms ± 1.19 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

这个对比说明，算法效率几乎从来不是一个简单的问题。适用于大数据集的高效算法，并不总是小数据集下的最佳选择，反之亦然。
但自己编写算法的优势在于：只要理解了这些基础方法，你就拥有了无限的可能性——不再受限于内置例程，可以创造属于自己的数据探索方式。
高效使用 python 进行数据密集型应用的关键，不仅在于了解像 np.histogram 这样的通用便捷函数及其适用场景，还在于当你需要更灵活的行为时，能够利用底层功能实现自定义操作。